Содержание
- 3. Треугольник Треугольник - простейшая плоская фигура. Три вершины и три стороны. Изучение треугольника породило науку –
- 4. Равносторонний Равнобедренный Разносторонний Классификация треугольников по сторонам Определи тип треугольника
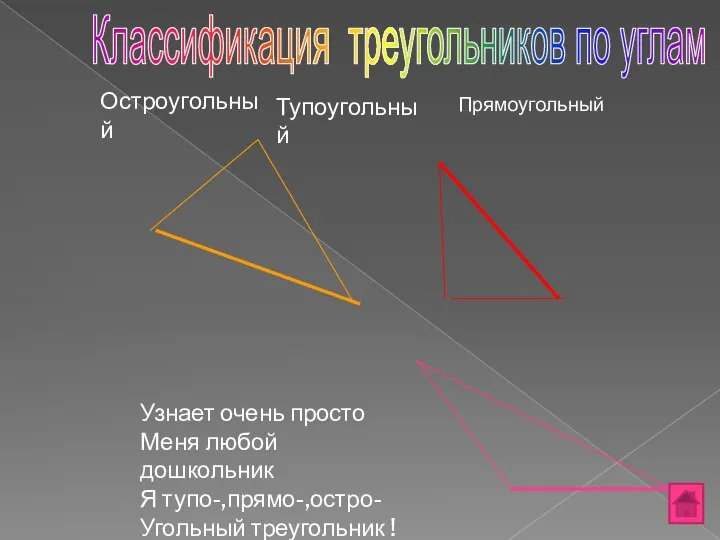
- 5. Остроугольный Узнает очень просто Меня любой дошкольник Я тупо-,прямо-,остро- Угольный треугольник ! Тупоугольный Классификация треугольников по
- 6. Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны (основанием
- 7. Медиана треугольника Отрезок соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Любой треугольник имеет
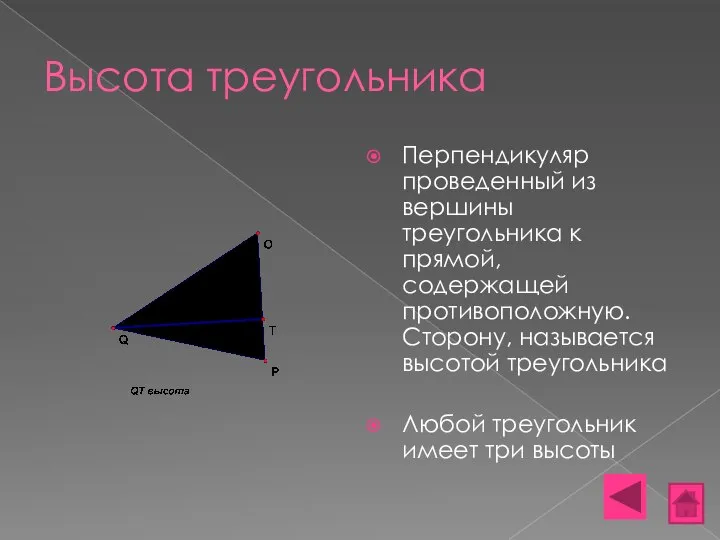
- 8. Высота треугольника Перпендикуляр проведенный из вершины треугольника к прямой, содержащей противоположную. Сторону, называется высотой треугольника Любой
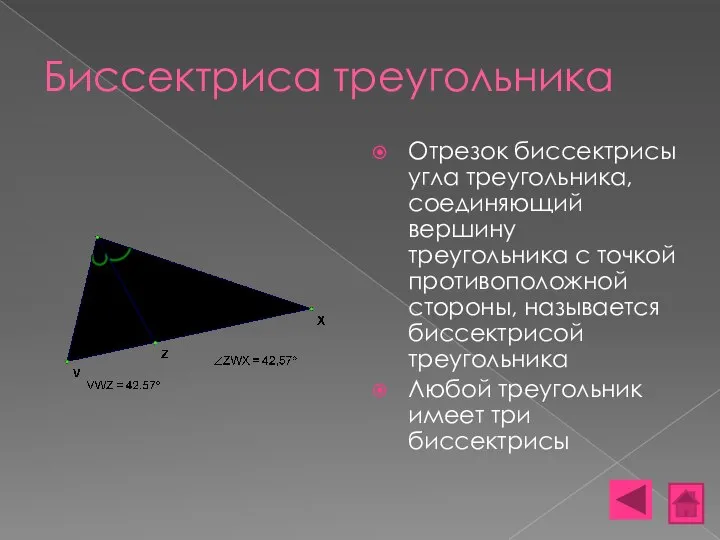
- 9. Биссектриса треугольника Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника
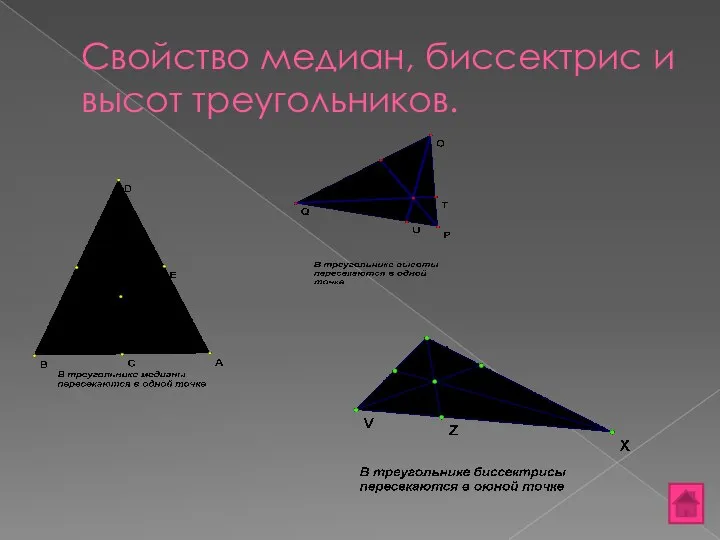
- 10. Свойство медиан, биссектрис и высот треугольников.
- 11. Теорема о сумме углов треугольника Теорема синусов , где R — радиус окружности, описанной вокруг треугольника.
- 12. Может ли в треугольнике быть два тупых угла Почему? Ответь на следующие вопросы Да Нет Может
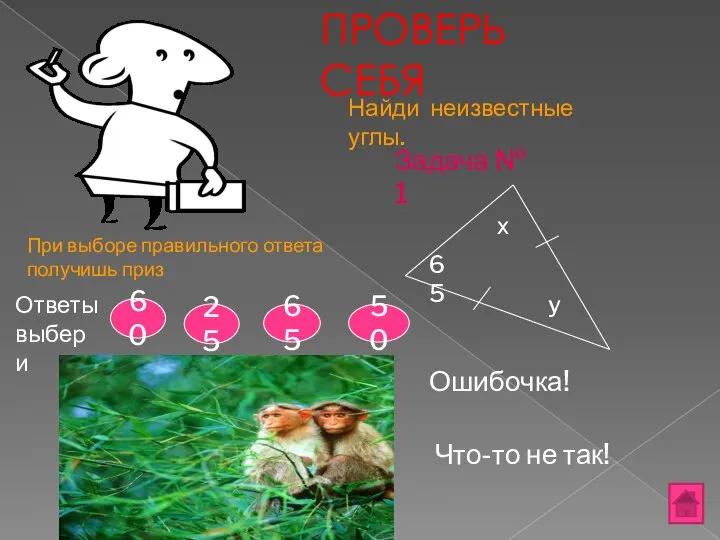
- 13. ПРОВЕРЬ СЕБЯ 65 y Ответы выбери х Задача № 1 Найди неизвестные углы. При выборе правильного
- 14. Первое упоминание о треугольнике и его свойствах мы находим в египетских папирусах Которым более 4000лет.Через 2000лет
- 16. Скачать презентацию







 Актуальность тематики исследований
Актуальность тематики исследований Площадь прямоугольника
Площадь прямоугольника Прямоугольный треугольник
Прямоугольный треугольник Презентация по математике "Веселый счет" - скачать
Презентация по математике "Веселый счет" - скачать  Вероятность получения положительной отметки при написании тестовой работы путем угадывания правильного ответа
Вероятность получения положительной отметки при написании тестовой работы путем угадывания правильного ответа Корреляционный анализ
Корреляционный анализ Действие с векторами. Уроки геометрии в 8 классе
Действие с векторами. Уроки геометрии в 8 классе Математическое описание случайных величин. (8 класс)
Математическое описание случайных величин. (8 класс) Веселая математика
Веселая математика Дифференцирование показательной и логарифмической функции. 11 класс
Дифференцирование показательной и логарифмической функции. 11 класс Проектирование условий измерений
Проектирование условий измерений Вариационный ряд. Полигон, гистограмма
Вариационный ряд. Полигон, гистограмма Сложение и вычитание двузначных чисел с переходом через десяток
Сложение и вычитание двузначных чисел с переходом через десяток Карточки по математике
Карточки по математике Министерство образования и науки Республики Бурятия МО «Кабанский район МОУ «Выдринская средняя общеобразовательная школ
Министерство образования и науки Республики Бурятия МО «Кабанский район МОУ «Выдринская средняя общеобразовательная школ Квадратная решётка, координатная плоскость. Многоугольники: вычисление площадей
Квадратная решётка, координатная плоскость. Многоугольники: вычисление площадей Отношения. Решение задач
Отношения. Решение задач Урок по алгебре в 11 классе Выполнила учительница математики МОУ «Аминевская СОШ» Юсупова Эльфия Лутфулловна 2006 год
Урок по алгебре в 11 классе Выполнила учительница математики МОУ «Аминевская СОШ» Юсупова Эльфия Лутфулловна 2006 год Решение задач на проценты. 5 класс. Урок № 5
Решение задач на проценты. 5 класс. Урок № 5 Признаки равенства треугольников
Признаки равенства треугольников Исследование модели многогранника с сечениями на примере куба
Исследование модели многогранника с сечениями на примере куба Правила записи сложных формул
Правила записи сложных формул Статистические критерии различий. (Лекция 3)
Статистические критерии различий. (Лекция 3) Сечения параллелепипеда. Геометрия. 10 класс. г. Екатеринбург. МАОУ-гимназия №13. Учитель математики Анкина Тамара Степановна.
Сечения параллелепипеда. Геометрия. 10 класс. г. Екатеринбург. МАОУ-гимназия №13. Учитель математики Анкина Тамара Степановна.  «Зимова спартакіада». Урок – гра
«Зимова спартакіада». Урок – гра Математическое моделирование. Значимость коэффициентов регрессии
Математическое моделирование. Значимость коэффициентов регрессии Basic transformations of graphs
Basic transformations of graphs Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен