Содержание
- 2. Три теоремы математической статистики Сначала рассмотрим три теоремы математической статистики. Их суть состоит в определении закона
- 3. Распределение χ2 (Хи-квадрат) Теорема 1. Если Xi - независимые СВ, подчиняющиеся нормальному закону распределения и у
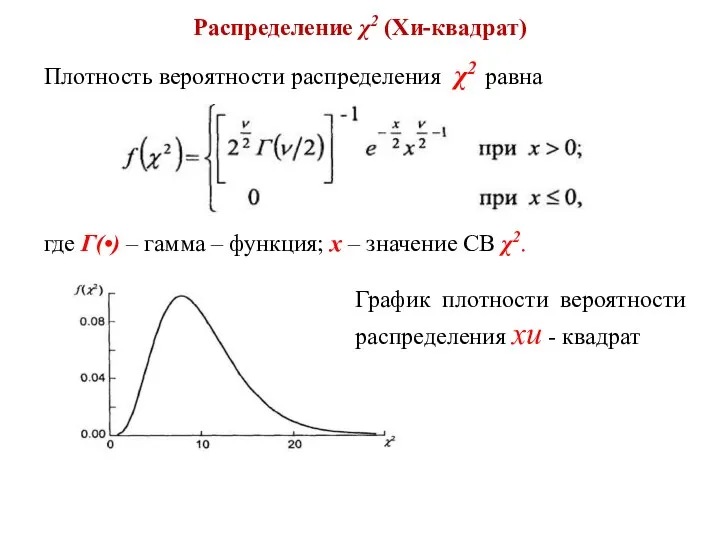
- 4. Распределение χ2 (Хи-квадрат) Плотность вероятности распределения χ2 равна где Г(•) – гамма – функция; х –
- 5. Распределение χ2 (Хи-квадрат) Математическое ожидание и дисперсия распределения χ2 равны: mx = ν и Dx =
- 6. Распределение χ2 (Хи-квадрат) В случае, если ν > 30, то можно использовать формулу где t’p –
- 7. Распределение χ2 (Хи-квадрат) В конечном итоге из изложенной выше теоремы следует, что (n-1)[S2x/σ2x] имеет распределение χ2
- 8. t - распределение (Стьюдента) Теорема 2. Если Z – нормированная нормально распределенная СВ, а U –
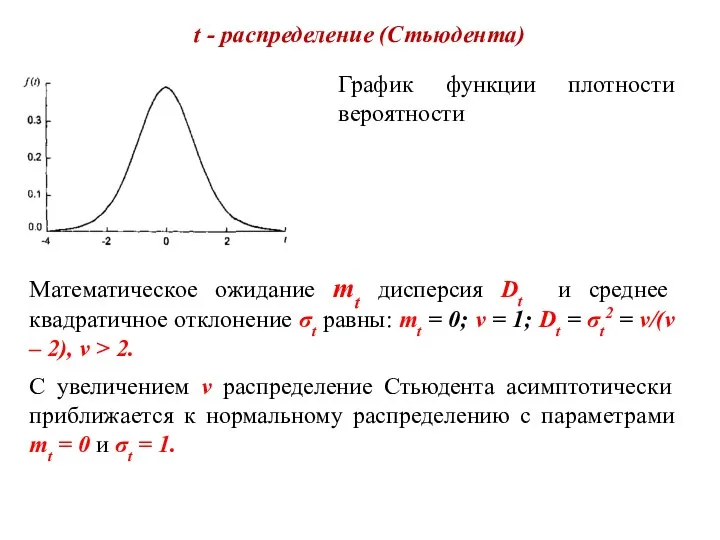
- 9. t - распределение (Стьюдента) Плотность вероятности этого распределения определяется равенством где с(ν) - параметр, зависящий от
- 10. t - распределение (Стьюдента) График функции плотности вероятности Математическое ожидание mt дисперсия Dt и среднее квадратичное
- 11. t - распределение (Стьюдента) Из этой теоремы следует, что величина (хср. - mx)/(S/√n) имеет распределение Стьюдента,
- 12. F – распределение (Фишера) Теорема 3. Если Z и U независимые СВ, обладающие χ2 распределением с
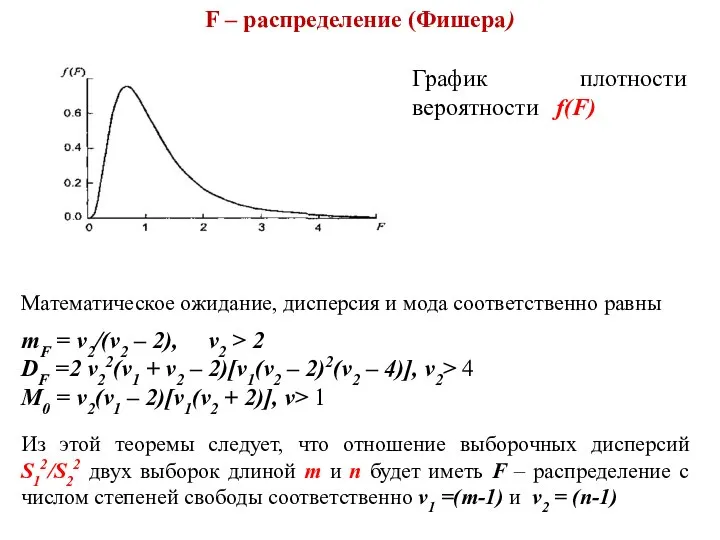
- 13. F – распределение (Фишера) Плотность вероятности F – распределения имеет вид где c1(ν1,ν2) – параметр, зависящий
- 14. F – распределение (Фишера) График плотности вероятности f(F) Математическое ожидание, дисперсия и мода соответственно равны mF
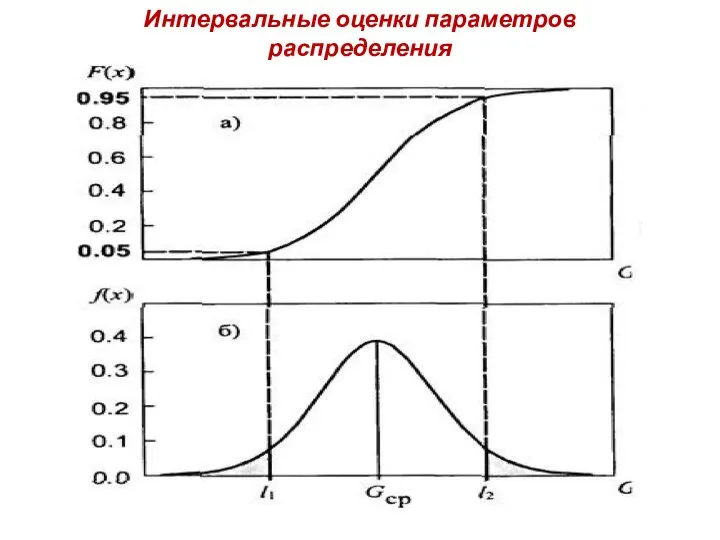
- 15. Интервальные оценки параметров распределения Интервальной оценкой параметра G называется интервал, границы которого l1* и l2* являются
- 16. Интервальные оценки параметров распределения Используя функцию распределения выборочных значений параметра G, можно записать вероятности не превышения
- 17. Интервальные оценки параметров распределения
- 18. Интервальная оценка математического ожидания На основании теоремы 2 выводится формула для интервальной оценки математического ожидания, а
- 19. Интервальная оценка математического ожидания Следовательно - t(1+p)/2 ≤ [(x-mx)/(Sx/√n)] После преобразования получаем
- 20. Интервальная оценка дисперсии Исходя из теоремы 1 можно записать, что где Sx2 = D* - выборочная
- 21. Интервальная оценка дисперсии Из этого выражения можно получить также интегральную оценку СКО.
- 23. Скачать презентацию













![Интервальная оценка математического ожидания Следовательно - t(1+p)/2 ≤ [(x-mx)/(Sx/√n)] После преобразования получаем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1467176/slide-18.jpg)


 Применение первообразной к нахождению площадей фигур
Применение первообразной к нахождению площадей фигур Взаимно обратные числа. 6 класс
Взаимно обратные числа. 6 класс Пересечение поверхностей. Способ вспомогательных секущих плоскостей
Пересечение поверхностей. Способ вспомогательных секущих плоскостей Обобщающий урок по теме: «ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ, ТАБЛИЦЫ ИСТИННОСТИ, ЛОГИЧЕСКИЕ СХЕМЫ»
Обобщающий урок по теме: «ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ, ТАБЛИЦЫ ИСТИННОСТИ, ЛОГИЧЕСКИЕ СХЕМЫ» Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Сумма n-первых членов геометрической прогрессии
Сумма n-первых членов геометрической прогрессии Приёмы быстрого счёта без калькулятора
Приёмы быстрого счёта без калькулятора Решение дифференциальных уравнений в частных производных
Решение дифференциальных уравнений в частных производных Общий прием сложения однозначных чисел с переходом через десяток
Общий прием сложения однозначных чисел с переходом через десяток Задачи на проценты
Задачи на проценты Решение задач по теме «Параллелограмм»
Решение задач по теме «Параллелограмм» Теория вероятностей в задачах ОГЭ-2022
Теория вероятностей в задачах ОГЭ-2022 Виды экспертных данных и способы их преобразований
Виды экспертных данных и способы их преобразований Равенство и неравенство. Устный счёт
Равенство и неравенство. Устный счёт Деление дробей Скрыбыкина Елена Петровна учитель математики МОУ «Кюсюрская СОШ» Булунского района Республики Саха(Якутия)
Деление дробей Скрыбыкина Елена Петровна учитель математики МОУ «Кюсюрская СОШ» Булунского района Республики Саха(Якутия)  Фрактальное множество Мандельброта
Фрактальное множество Мандельброта Счет от 0 до 20
Счет от 0 до 20 Правильные многогранники
Правильные многогранники Нахождение дроби числа
Нахождение дроби числа Уравнения. 5 класс
Уравнения. 5 класс Презентация на тему Обозначение натуральных чисел. 5 класс.
Презентация на тему Обозначение натуральных чисел. 5 класс.  Теорема Пифагора
Теорема Пифагора Квадратура круга
Квадратура круга Решение задач с помощью систем уравнений
Решение задач с помощью систем уравнений Интегралы функции одной переменной
Интегралы функции одной переменной Решение заданий с параметром. Занятие №1
Решение заданий с параметром. Занятие №1 Практичне застосування перетворення Фур’є
Практичне застосування перетворення Фур’є 20171119_ploskost._pryamaya._luch
20171119_ploskost._pryamaya._luch