Содержание
- 2. Испытания Бернулли. Формула Бернулли Ответ на 1-й вопрос дает формула Бернулли: - вероятность наступления события k
- 3. Число сочетаний
- 4. Испытания Бернулли. Формула Бернулли При ответе на 2-й вопрос по существу требуется определить наивероятнейшее число k0
- 5. Испытания Бернулли. Формула Бернулли Можно показать, что эти условия приводят к неравенству Замечания: 1. k0 –
- 6. Испытания Бернулли. Формула Бернулли Задача. Монета брошена 5 раз. Какова вероятность того, что герб появится ровно
- 7. Испытания Бернулли. Формула Бернулли 2. Найдем k0 из неравенства с учетом n = 5 и p
- 8. Испытания Бернулли. Формула Бернулли Т.о. имеем два наивероятнейших числа: Поэтому должно быть Убедимся в этом:
- 9. Использование противоположного события При независимых многократных испытаниях для вычисления вероятности суммы событий вместо теоремы сложения вероятностей
- 10. Использование противоположного события Пусть – наступление события A в i-м испытании. По определению, сумма событий –
- 11. Использование противоположного события Противоположные события составляют полную группу, поэтому сумма их вероятностей равна единице, т. е.
- 12. Использование противоположного события По теореме умножения вероятностей независимых событий где . Итак,
- 13. Использование противоположного события Задача. Три стрелка стреляют в цель с вероятностью успеха Найти вероятность поражения мишени.
- 14. Использование противоположного события Событие Вычислим вероятности противоположных событий:
- 15. Использование противоположного события Тогда вероятность события B:
- 16. Распределения дискретных случайных величин Все процессы, происходящие в природе, делятся на непрерывные и дискретные. Например, такие
- 17. Рассмотрим вероятностное пространство (Ω, σ, Р), то есть пространство элементарных исходов Ω, σ -алгебру событий (определенную
- 18. Случайной величиной ξ (кси) называется произвольная функция, ставящая в соответствие каждому элементарному исходу (событию) ω число
- 19. Распределение дискретной случайной величины ξ
- 20. Пример Два игрока играют в “орлянку” на следующих условиях: если при подбрасывании монеты выпадает “орел”, то
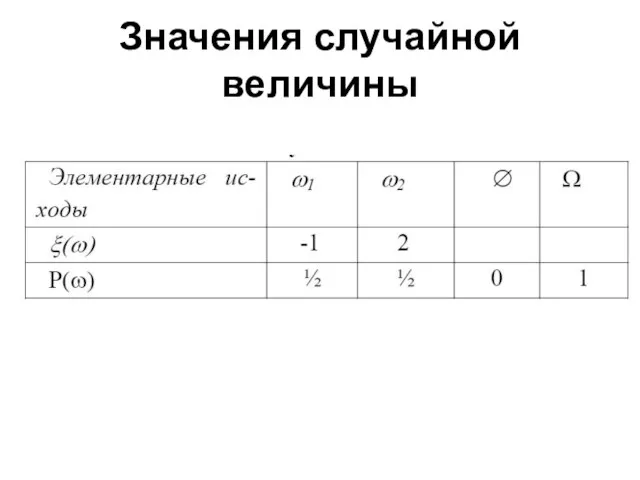
- 21. Решение Пространство элементарных исходов (событий) Ω состоит из двух исходов: ω1 – выпадение “орла” и ω2
- 22. Значения случайной величины
- 23. Функция распределения случайной величины Функцией распределения (вероятностей) случайной величины ξ называется функция F(x), значение которой в
- 24. Свойства функции распределения 1. Функция F(x) является ограниченной, то есть ее значения лежат в интервале от
- 25. 3. Вероятность попадания случайной величины ξ на отрезок (x1, x2) определяется формулой: P{x1 ≤ ξ ≤
- 26. Ряд распределения дискретной случайной величины числа выпавших очков при бросании кости
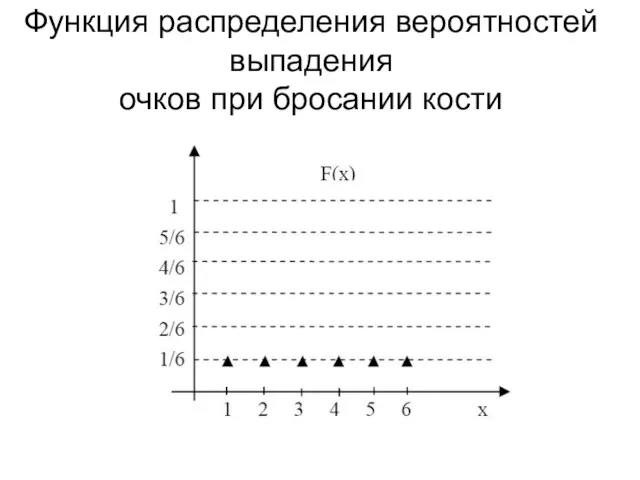
- 27. Функция распределения вероятностей выпадения очков при бросании кости
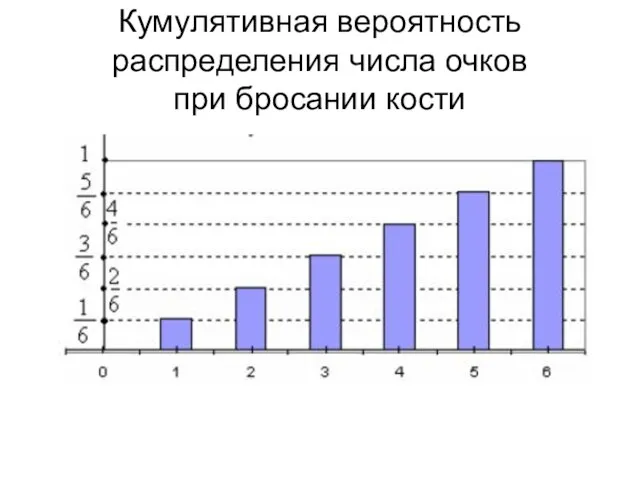
- 28. Кумулятивная вероятность распределения числа очков при бросании кости
- 29. Пример В неком обществе организована лотерея. Разыгрываются две вещи стоимостью по $10 и одна стоимостью $30.
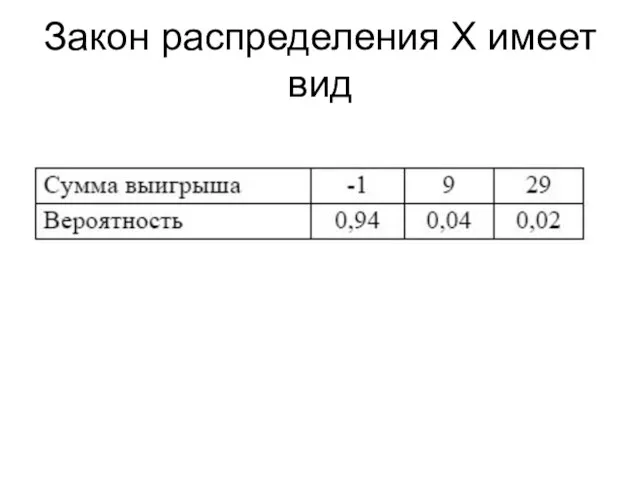
- 30. Решение Искомая случайная величина X может принимать три значения: -1, (если субъект не выиграет, а проиграет
- 31. Закон распределения Х имеет вид
- 32. Виды распределений
- 33. Биноминальное распределение является распределением числа успехов μ в n испытаниях Бернулли с вероятностью успеха p и
- 34. Схема Бернулли Рассмотрим последовательность независимых одинаковых испытаний: появление или не появление некоторого наблюдаемого события в каждом
- 35. Результат каждого опыта можно записать в виде последовательности УНН...У, “У” – успех, “Н” – неудача. Пространство
- 36. В силу независимости испытаний сопоставим каждому элементарному исходу ω = УННУ...У вероятность Р(ω) = Р(УННУ...У)= pqqp...p,
- 37. Вероятность Рn(m) получить в n испытаниях ровно m успехов. Данное выражение носит также название биноминального закона,
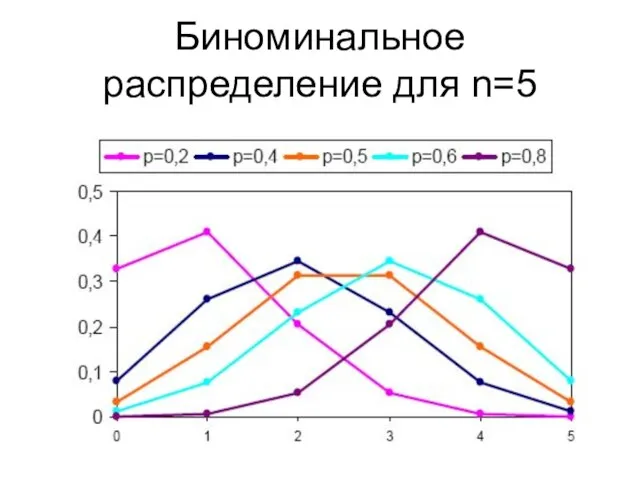
- 38. Биноминальное распределение для n=5
- 39. Пример Монета брошена 2 раза. Определить закон распределения случайной величины Х – числа выпадений герба.
- 40. При бросании монеты герб может появиться или 2 раза или 1 раз или совсем не появиться.
- 42. Пример На зачете студент получил n = 4 задачи. Вероятность решить правильно каждую задачу p =
- 43. В данном случае мы имеем дело с биноминальным законом:
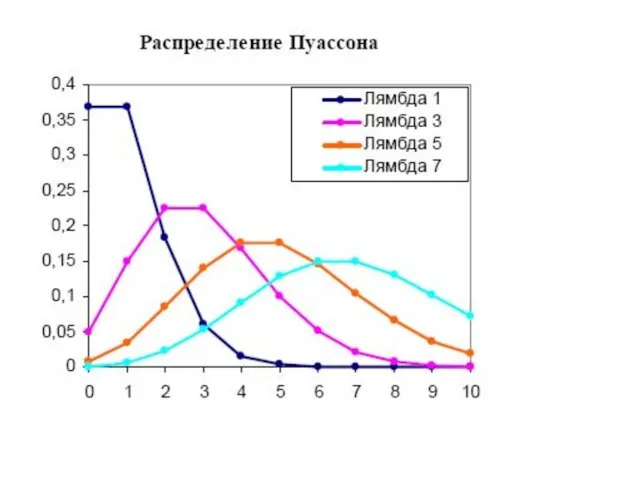
- 44. Пуассоновское распределение Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при
- 45. Параметр пуассоновского распределения λ>0 определяет интенсивность поступления событий и определяется формулой: λ =n*p, где n –
- 46. Распределение Пуассона носит также название закона редких событий, поскольку оно всегда появляется там, где производится большое
- 48. Формула Пуассона Формула Пуассона применяется тогда, когда наряду с большим значением числа испытаний n “мала” вероятность
- 49. Пример Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится равно
- 50. По условию n =5000, р=0,0002, k=3. Найдем λ= np =5000*0.0002=1 По формуле Пуассона искомая вероятность равна
- 51. Пример Среднее число вызовов, поступающих на АТС в одну минуту, равно – 2. Найти вероятности того,
- 52. по условию λ=2, t=5, m=4. По формуле Пуассона: А) Вероятность, что за 5 минут поступят 2
- 53. Б) События «не поступило не одного вызова» и «поступил 1 вызов» – несовместны, поэтому по теореме
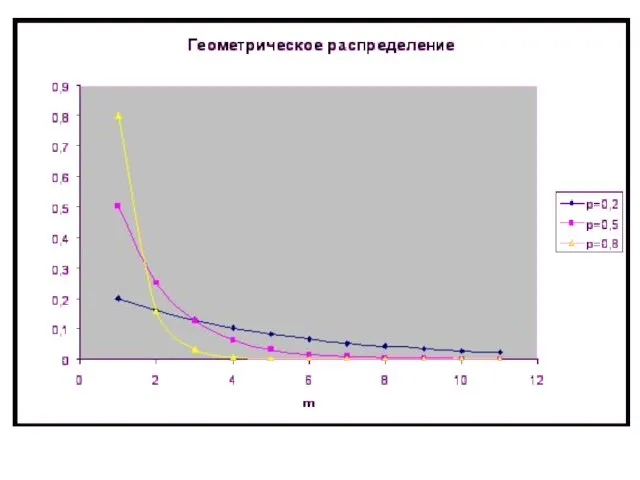
- 54. Геометрическое распределение Пусть ξ – число испытаний, которое необходимо провести, прежде чем появится первый успех. Тогда
- 56. Пример Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р=0,6. Найти
- 57. По условию, р=0,6, q=0,4, k=3. Искомая вероятность определяется по формуле:
- 58. Продолжение примера Производится стрельба по мишени до первого попадания (число патронов не ограничено). Требуется составить ряд
- 59. Случайная величина X – число сделанных выстрелов – имеет геометрическое распределение с параметром p=0,6. Ряд распределения
- 60. Гипергеометрическое распределение Дискретная случайная величина X имеет гипергеометрическое распределение, если она принимает значения 0,1, 2, ...,
- 61. где m=1, 2, ..., min {n, M}, m≤N, n≤N; n, N, M – натуральные числа. N
- 62. Гипергеометрическое распределение широко используется в практике статистического приёмочного контроля качества промышленной продукции, в задачах, связанных с
- 63. Пример В национальной лотерее "6 из 45" денежные призы получают участники, угадавшие от трёх до шести
- 64. Случайная величина X – число угаданных чисел среди случайно отобранных шести – имеет гипергеометрическое распределение с
- 66. Скачать презентацию

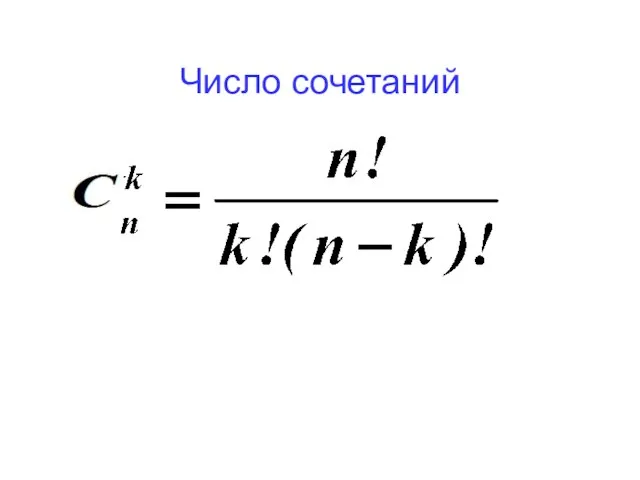






















































 Степень с рациональным показателем
Степень с рациональным показателем Аттестационная работа. Математические задачи о г. Химки
Аттестационная работа. Математические задачи о г. Химки Уравнения и неравенства с параметрами. Часть 1
Уравнения и неравенства с параметрами. Часть 1 Объем пирамиды
Объем пирамиды Көбейтудің қосуға қарағандағы үлестірімділік қасиеті
Көбейтудің қосуға қарағандағы үлестірімділік қасиеті Понятие множества. Способы задания множеств. Операции над множествами
Понятие множества. Способы задания множеств. Операции над множествами Корень n-й степени
Корень n-й степени Сфера и шар
Сфера и шар Построение графика квадратичной функции. Готовимся к ГИА
Построение графика квадратичной функции. Готовимся к ГИА Логика. Эквиваленция
Логика. Эквиваленция Работу выполнила Артамонова Лариса Владимировна - учитель математики первой квалификационной категории, МОУ «Москаленский
Работу выполнила Артамонова Лариса Владимировна - учитель математики первой квалификационной категории, МОУ «Москаленский  Пирамида. Задачи ЕГЭ
Пирамида. Задачи ЕГЭ Презентация по математике "Олимпийские игры и математика" - скачать
Презентация по математике "Олимпийские игры и математика" - скачать  Переводы чисел из одной системы счисления в другую
Переводы чисел из одной системы счисления в другую Пирамида. Решение задач
Пирамида. Решение задач Способи представлення графів
Способи представлення графів Постройте сечение куба и тетраэдра
Постройте сечение куба и тетраэдра Понятие определенного интеграла
Понятие определенного интеграла Действительный анализ. Глава 2. Измеримые множества
Действительный анализ. Глава 2. Измеримые множества Задачи на дроби
Задачи на дроби Мир геометрии
Мир геометрии Природа глазами математики
Природа глазами математики Основные формулы к задачам типа В9
Основные формулы к задачам типа В9 Урок математики в 6 классе
Урок математики в 6 классе Производная степенной функции УРОК алгебры и начала анализа в 11 «Б» классе учителя лицея № 179 ПАК НАТАЛЬИ НИКОЛАЕВНЫ
Производная степенной функции УРОК алгебры и начала анализа в 11 «Б» классе учителя лицея № 179 ПАК НАТАЛЬИ НИКОЛАЕВНЫ  Бөлшектік еселікпен резервтеу. Көпшілік дауыс беру бойынша резервтеу. Лекция №5
Бөлшектік еселікпен резервтеу. Көпшілік дауыс беру бойынша резервтеу. Лекция №5 Перпендикуляр и наклонные. Угол между прямой и плоскостью
Перпендикуляр и наклонные. Угол между прямой и плоскостью Арифметический диктант
Арифметический диктант