Содержание
- 2. §1 Способи представлення графів Графічне задання – відображення графа за допомогою точок і ліній; Матриця суміжності
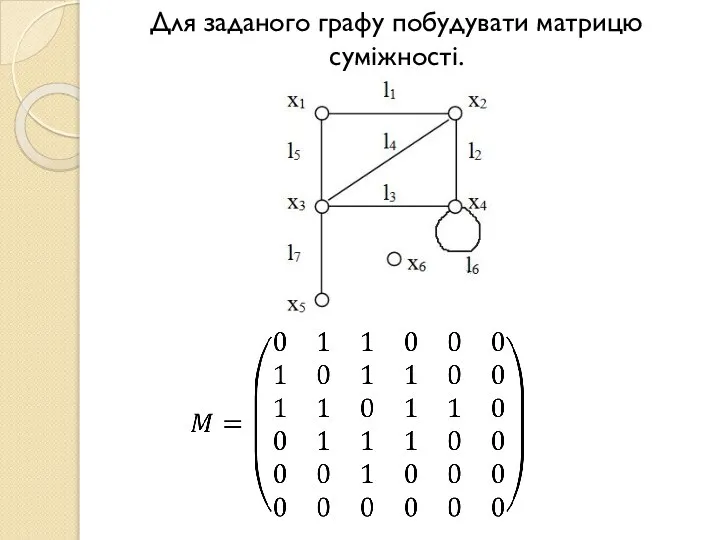
- 3. 1.1 Матриця суміжності Матрицею суміжності графа G , яка відповідає заданій нумерації вершин, називають булеву квадратну
- 4. Для заданого графу побудувати матрицю суміжності.
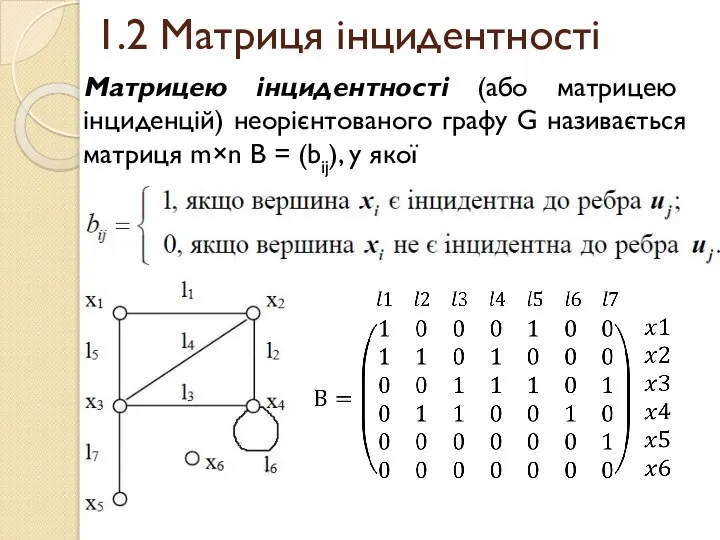
- 5. 1.2 Матриця інцидентності Матрицею інцидентності (або матрицею інциденцій) неорієнтованого графу G називається матриця m×n В =
- 6. 1.3 Список суміжних вершин Список суміжних вершин – це масив A[n], кожен елемент A[i] якого містить
- 7. Реалізація списку суміжних вершин на основі масивів A[n+1] та L[2m].
- 8. 1.4 Список ребер Пара [u, v] відповідає ребру {u,v}, якщо граф неорієнтований, і дузі (u,v), якщо
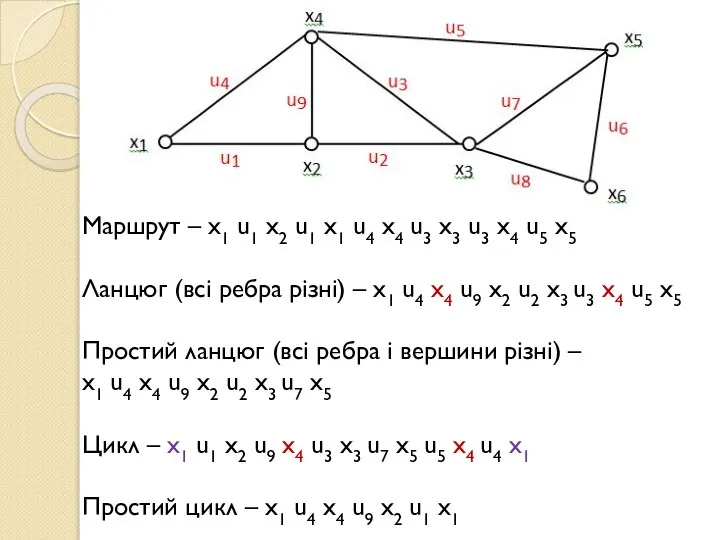
- 9. §2 Маршрути, ланцюги та цикли Нехай G= (X, U) – скінченний неорієнтований граф. Скінчена послідовність вершин
- 10. Маршрут, в якому всі ребра є різні, називають ланцюгом. Замкнений ланцюг називають циклом. Ланцюг називають простим,
- 11. Маршрут – x1 u1 x2 u1 x1 u4 x4 u3 x3 u3 x4 u5 x5 Ланцюг
- 12. §3 Орієнтовані графи Поняття орієнтованого графа (орграфа) виникає, якщо ребрам графа надати напрямок (тобто орієнтацію) в
- 13. Орієнтований граф G = (X,U), де X = {x1, x2, x3, x4, x5}; U = {(x1,
- 14. §4 Способи задання орієнтованих графів 4.1 Матриця суміжності Матрицею суміжності орграфа G називається квадратна матриця А(G)
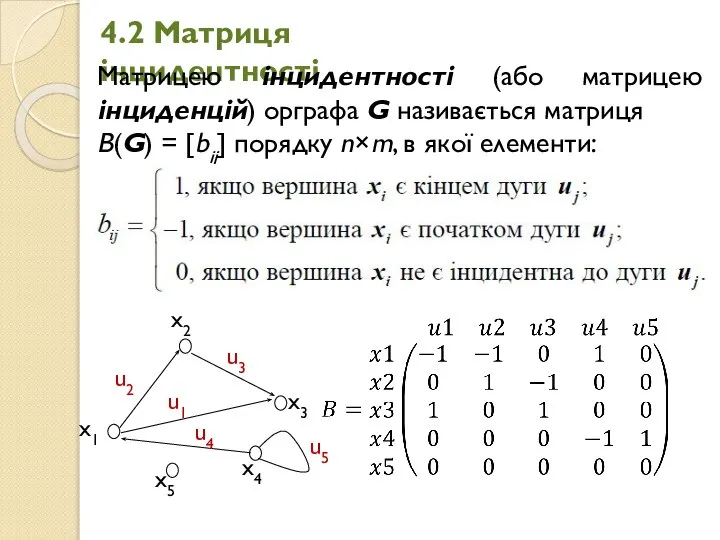
- 15. 4.2 Матриця інцидентності Матрицею інцидентності (або матрицею інциденцій) орграфа G називається матриця B(G) = [bij] порядку
- 16. Матрицю суміжності можна визначити і для псевдографів. Тоді в разі орієнтованого (неорієнтованого) псевдографа aij=k, де k
- 17. §5 Маршрути, шляхи та контури орієнтованого графа Орієнтовані маршрути: в орграфі рух за маршрутом допускається лише
- 19. Скачать презентацию


![1.3 Список суміжних вершин Список суміжних вершин – це масив A[n],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1457902/slide-5.jpg)
![Реалізація списку суміжних вершин на основі масивів A[n+1] та L[2m].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1457902/slide-6.jpg)
![1.4 Список ребер Пара [u, v] відповідає ребру {u,v}, якщо граф](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1457902/slide-7.jpg)







 Аттестационная работа. Разработка программы дополнительного образования по математике 5 класс «Прикладная математика»
Аттестационная работа. Разработка программы дополнительного образования по математике 5 класс «Прикладная математика» B13 ЕГЭ 2013г. Болкисева Гульнара Марсельевна
B13 ЕГЭ 2013г. Болкисева Гульнара Марсельевна Иррациональные уравнения
Иррациональные уравнения Прогрессии. Вид последовательности
Прогрессии. Вид последовательности История Кремля в математике и литературе
История Кремля в математике и литературе Презентация на тему Решето Эратосфена
Презентация на тему Решето Эратосфена  Работа со способными детьми и олимпиады
Работа со способными детьми и олимпиады Задания по геометрии
Задания по геометрии Аттестационная работа. Программа курса по выбору по математике Реальная математика для учащихся 7 класса
Аттестационная работа. Программа курса по выбору по математике Реальная математика для учащихся 7 класса Функции многих переменных (ФМП). Частные производные функции двух переменных
Функции многих переменных (ФМП). Частные производные функции двух переменных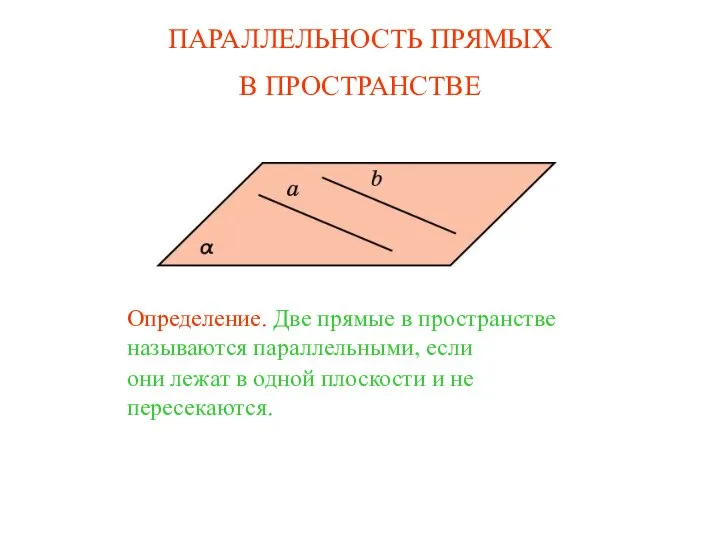 Параллельность прямых в пространстве
Параллельность прямых в пространстве Презентация на тему Табличное умножение и деление
Презентация на тему Табличное умножение и деление  Додавання раціональних чисел
Додавання раціональних чисел Формулы сокращенного умножения
Формулы сокращенного умножения Мой любимый предмет – геометрия. «Геометрия – прообраз красоты мира.» И. Кеплер. 11 класс
Мой любимый предмет – геометрия. «Геометрия – прообраз красоты мира.» И. Кеплер. 11 класс Координатная плоскость
Координатная плоскость Устойчивость сжатых стержней (продольный изгиб). Формула Эйлера
Устойчивость сжатых стержней (продольный изгиб). Формула Эйлера Система обучения алгебре, направленная на формирование функциональной грамотности у обучающихся
Система обучения алгебре, направленная на формирование функциональной грамотности у обучающихся Формирование метапредметного умения «Решать проблемы и задачи» на уроках математики
Формирование метапредметного умения «Решать проблемы и задачи» на уроках математики Использование свойств действий при вычислениях. Наглядный материал к уроку
Использование свойств действий при вычислениях. Наглядный материал к уроку Великолепный часослов герцога Беррийского. Математика в каждом
Великолепный часослов герцога Беррийского. Математика в каждом Понятие предела функции. Бесконечно малая и бесконечно большая функции
Понятие предела функции. Бесконечно малая и бесконечно большая функции арифметическая прогрессия. Решение задач. 9 класс
арифметическая прогрессия. Решение задач. 9 класс Презентация к уроку математики 1 класс по теме: «Числа от нуля до 10» урок №88 (по курсу Б. П. Гейдман) Выполнила Алексеенко Галина Але
Презентация к уроку математики 1 класс по теме: «Числа от нуля до 10» урок №88 (по курсу Б. П. Гейдман) Выполнила Алексеенко Галина Але Первообразная и неопределённый интеграл
Первообразная и неопределённый интеграл Теорема синусов
Теорема синусов СУММА УГЛОВ ТРЕУГОЛЬНИКА
СУММА УГЛОВ ТРЕУГОЛЬНИКА Демоверсия ГИА 2011 год Учитель ОУ СОШ №19 Лурда Л.Н.
Демоверсия ГИА 2011 год Учитель ОУ СОШ №19 Лурда Л.Н.