Понятие определенного интеграла

Интегральное исчисление и само понятие интеграла возникли из необходимости вычисления площадей

«метод исчерпывания»
Метод заключался в следующем: для нахождения площади (или объёма) некоторой

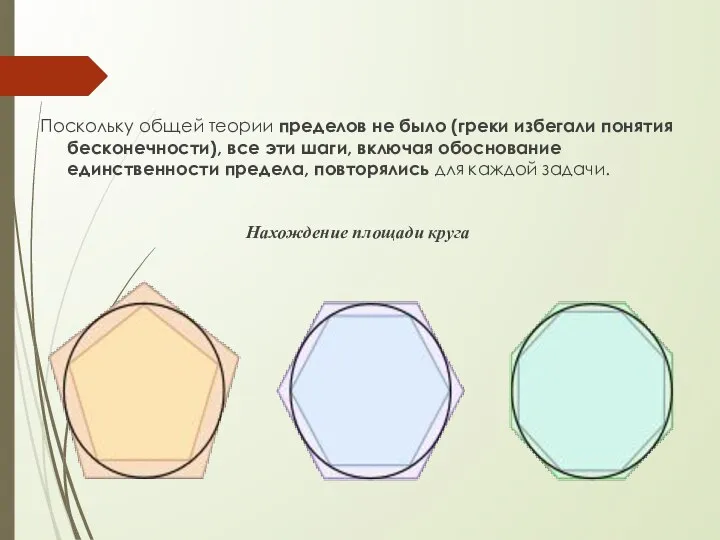
Поскольку общей теории пределов не было (греки избегали понятия бесконечности), все

Попробуем решить задачу

Найдем площадь изображения рыбки
Как нам действовать?

В это изображение мы попробуем вписать фигуры, площадь которых мы сможем

Возникают вопросы:
Насколько точно мы вычислим площадь этого изображения?
И Как

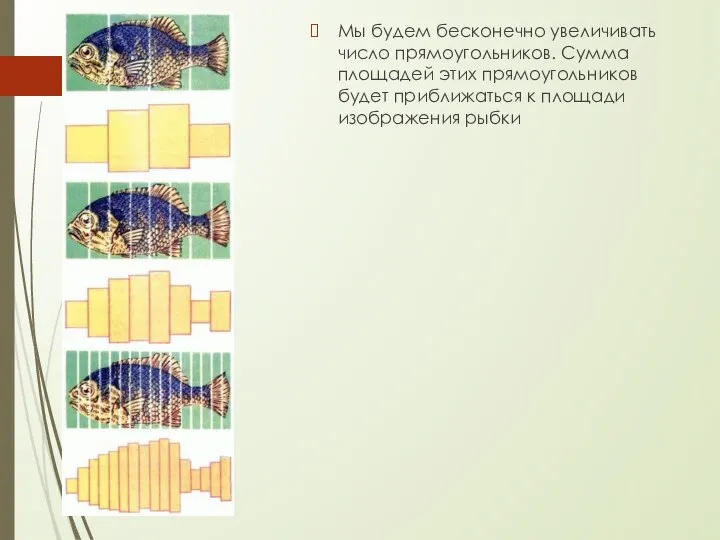
Мы будем бесконечно увеличивать число прямоугольников. Сумма площадей этих прямоугольников будет

Чем меньше будут прямоугольники , тем точнее мы сможем найти площадь

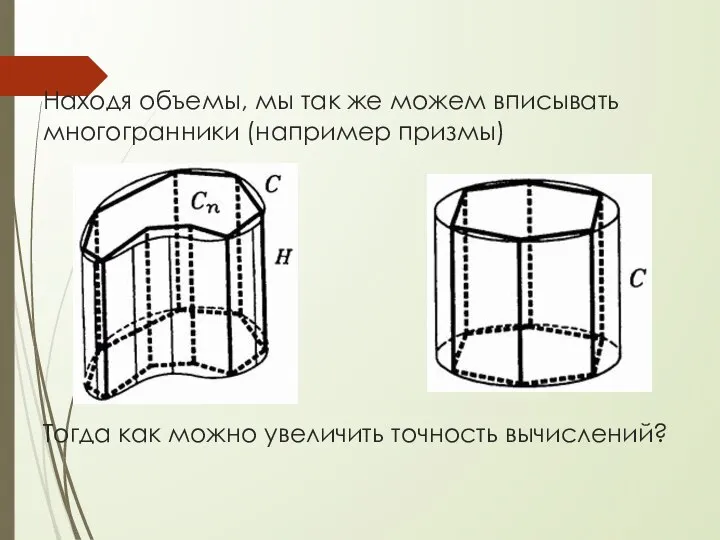
Находя объемы, мы так же можем вписывать многогранники (например призмы) Тогда как

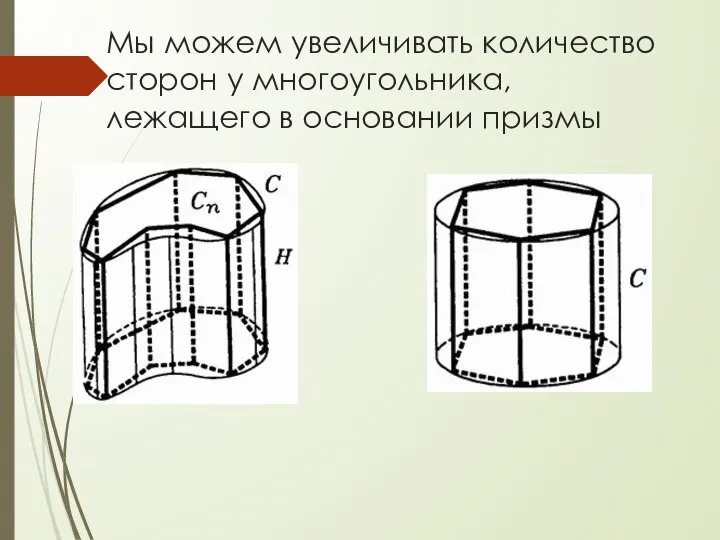
Мы можем увеличивать количество сторон у многоугольника, лежащего в основании призмы

Метод исчерпывания хорошо вписывался в строго дедуктивное построение античной математики,

Архимед еще явным
образом не применял
общее понятие предела
и интеграла,

В ХVІІ в.Йоганн Кеплер (1571 – 1630)
1. открыл законы движения

«Поскольку бочки связаны с кругом, конусом и цилиндром – фигурами правильными,

Рассказывают, что когда Кеплер покупал вино для свадьбы, он был изумлен

Кеплера заинтересовало, насколько точно торговец определял объем бочки при помощи всего

Вначале Кеплер нашел формулу для вычисления объема бочки, а затем —

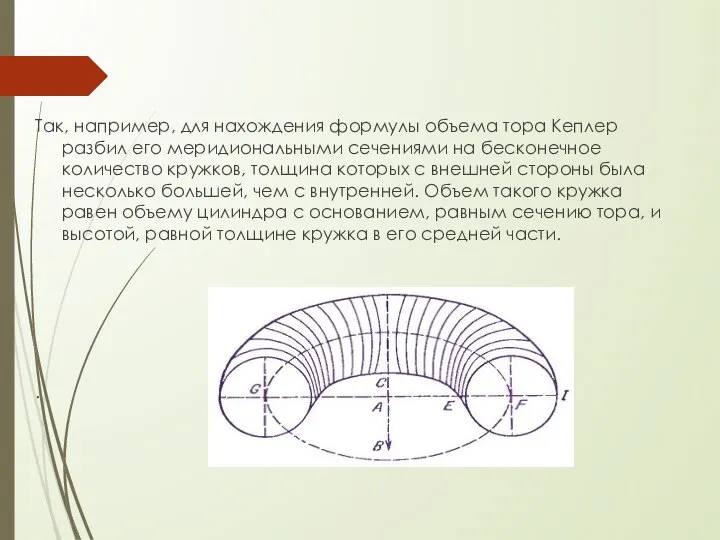
Так, например, для нахождения формулы объема тора Кеплер разбил его меридиональными

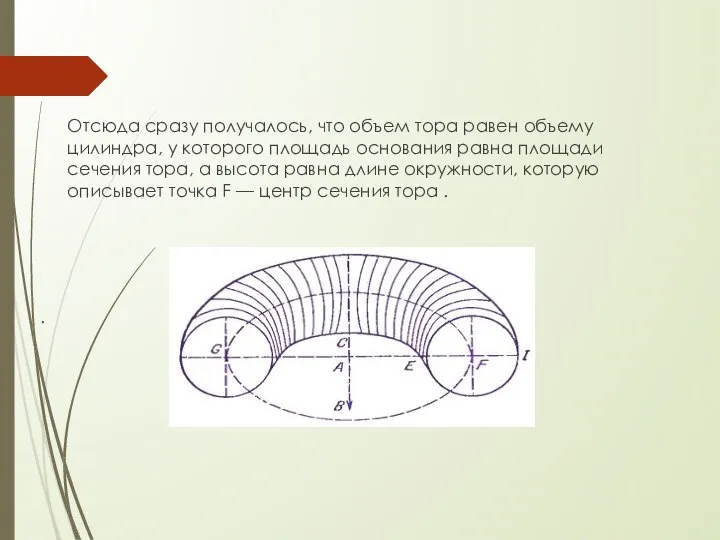
Отсюда сразу получалось, что объем тора равен объему цилиндра, у которого

Математика за чайным столом

Чтобы получить представление об этих общих методах, попробуем

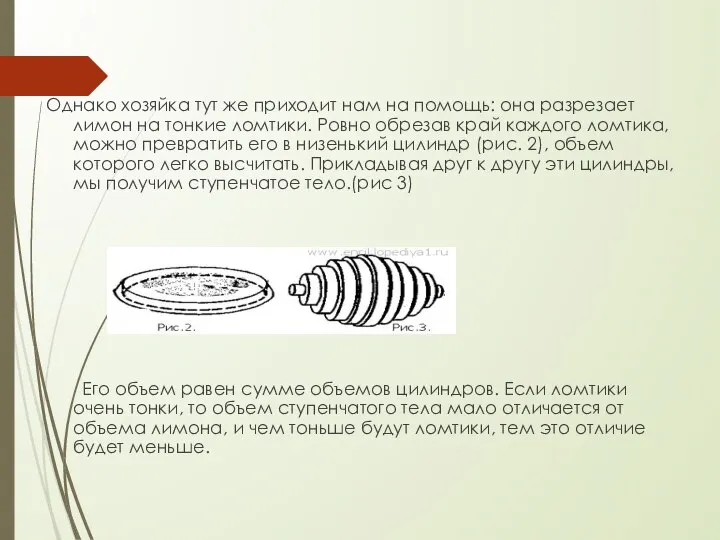
Однако хозяйка тут же приходит нам на помощь: она разрезает лимон

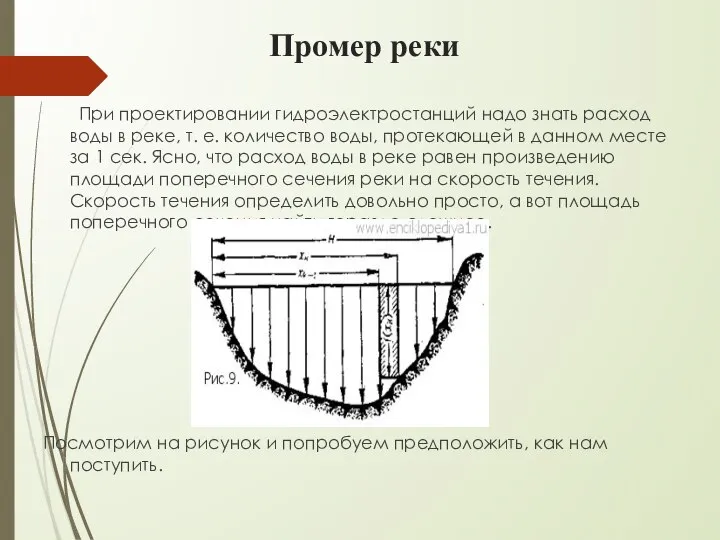
Промер реки

При проектировании гидроэлектростанций надо знать расход воды в реке, т.

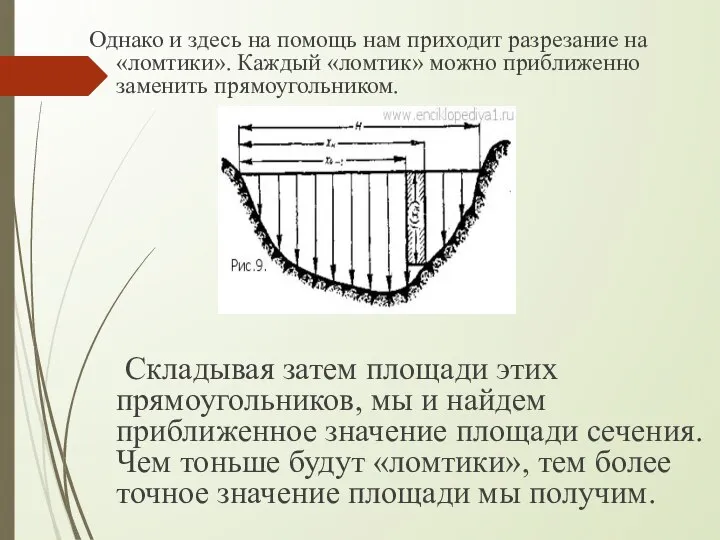
Однако и здесь на помощь нам приходит разрезание на «лом­тики». Каждый

итальянский математик
Бонавентуро Кавальере
(1598 – 1647)
пересекая фигуру (тело) параллельными прямыми

Иллюстрация принципа Кавальери
Объемы (или площади) двух фигур равны, если равны между собой площади (или длины)  всех соответственных их сечений,
  проведенных параллельно некоторой 
данной плоскости (или прямой).

Примеры применения метода  неделимых Найти объем призмы или найти площадь круга

Найдем площадь круга
Посмотрим как применяется метод неделимых при решении этой задачи…

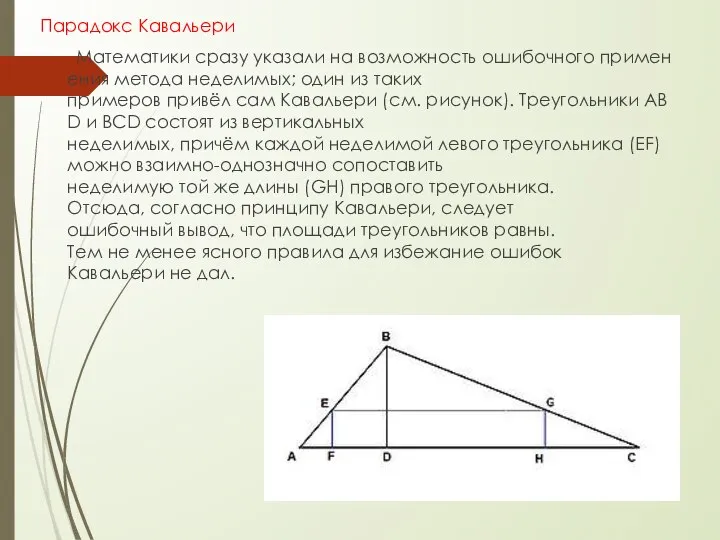
Парадокс Кавальери
Математики сразу указали на возможность ошибочного применения метода неделимых; один из таких примеров привёл сам Кавальери (см. рисунок). Треугольники ABD и BCD состоят из вертикальных неделимых, причём каждой неделимой левого треугольника (EF) можно взаимно-однозначно сопоставить неделимую той же длины (GH) правого треугольника.  Отсюда, согласно принципу Кавальери, следует ошибочный вывод, что площади треугольников равны. Тем не менее ясного правила для избежание ошибок  Кавальери не дал.

Кавальери был наиболее ярким и влиятельным представителем «геометрии неделимых»  . В

Однако при всей значимости результатов, полученных математиками XVII столетия, исчисления  еще не было. Необходимо

Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт,

Символ интеграла введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы

Давайте введем понятие определенного интеграла

В школе к понятию определенного интеграла нас

Рассматривалась непрерывная неотрицательная функция y = f(x) на отрезке [a; b]
.Вспомним материал нашего урока,

Верно, мы будем разбивать эту фигуру.
Отрезок [a; b] разбиваем на n равных частей

и соответствующая площадь криволинейной трапеции приближенно представлялась суммой площадей элементарных прямоугольников Но

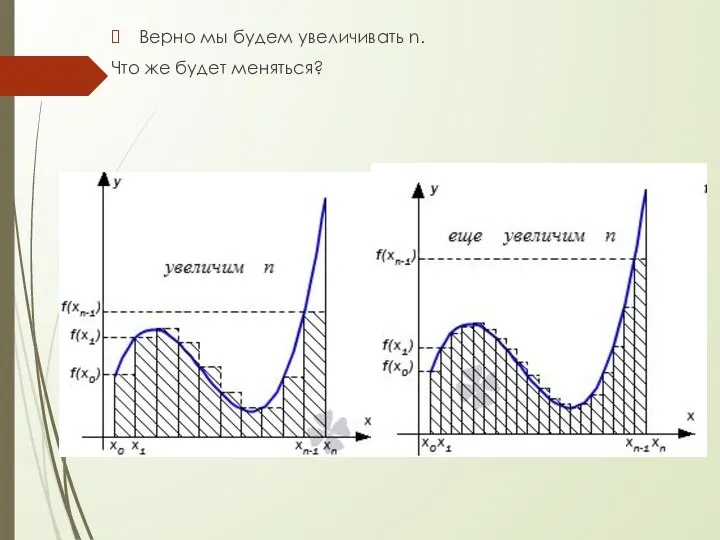
Верно мы будем увеличивать n.
Что же будет меняться?

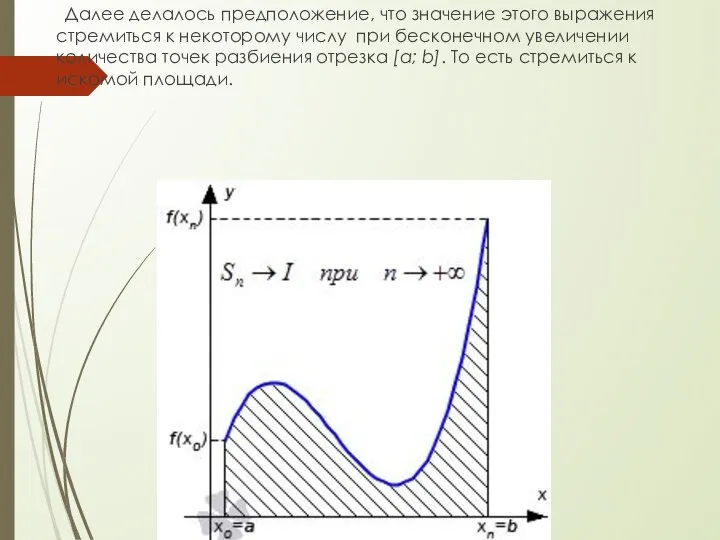
Далее делалось предположение, что значение этого выражения стремиться к некоторому числу  при