Содержание
- 2. 1) степенные функции y = xk, где k – любое действительное число; 2) показательные функции y
- 3. Функции, получающиеся из основных элементарных функций с помощью конечного числа арифметических операций и операции образования сложной
- 4. Линейная функция Линейной функцией называют функцию вида y = ax + b. (1) При b =
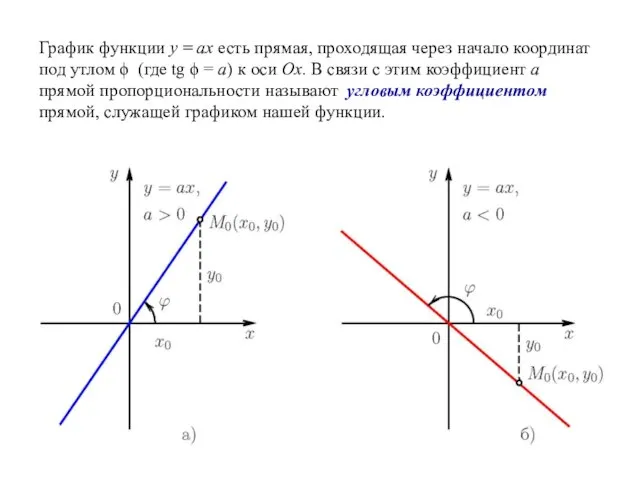
- 5. График функции у = ах есть прямая, проходящая через начало координат под утлом ϕ (где tg
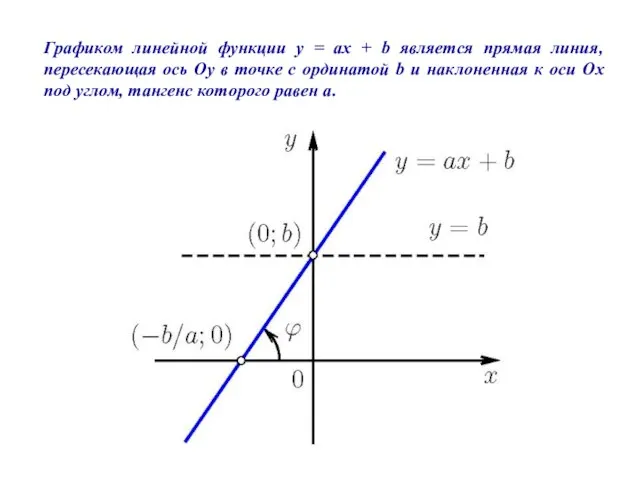
- 6. Графиком линейной функции y = ax + b является прямая линия, пересекающая ось Оу в точке
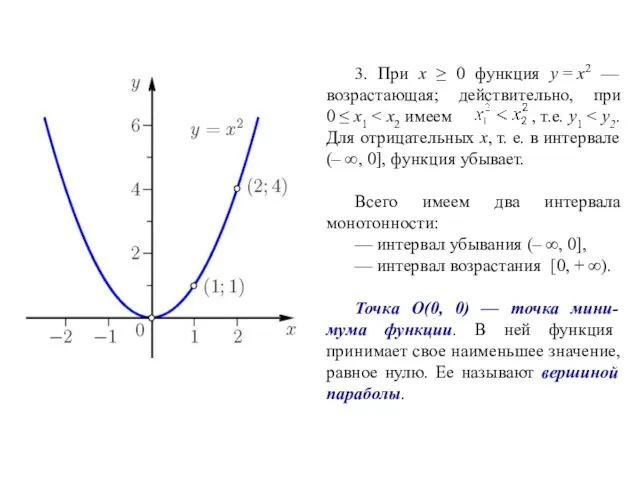
- 7. Квадратичная функция Рассмотрим функцию у = х2, установим ее простейшие свойства и построим график этой функции.
- 8. 3. При х ≥ 0 функция у = х2 — возрастающая; действительно, при 0 ≤ х1
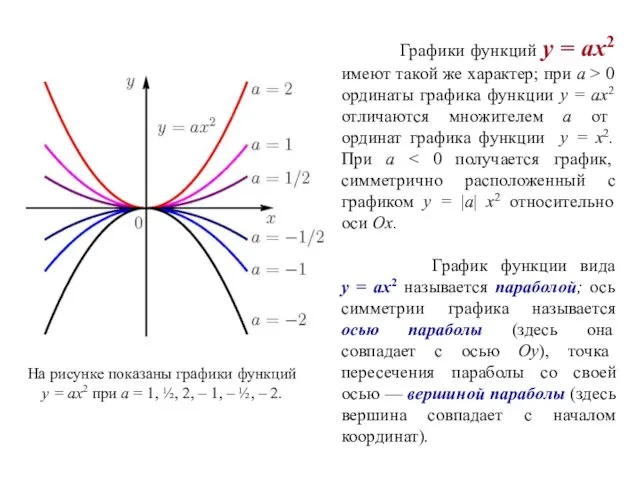
- 9. Графики функций у = ах2 имеют такой же характер; при а > 0 ординаты графика функции
- 10. Степенная функция Рассмотрим теперь функцию у = хп при любом натуральном п. Некоторые общие свойства рассматриваемых
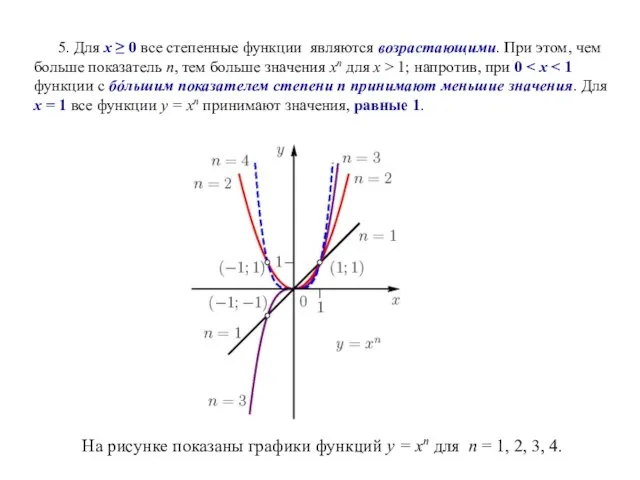
- 11. 5. Для х ≥ 0 все степенные функции являются возрастающими. При этом, чем больше показатель п,
- 12. Обратная пропорциональная зависимость В этом случае говорят, что х и у находятся в обратной пропорциональной зависимости,
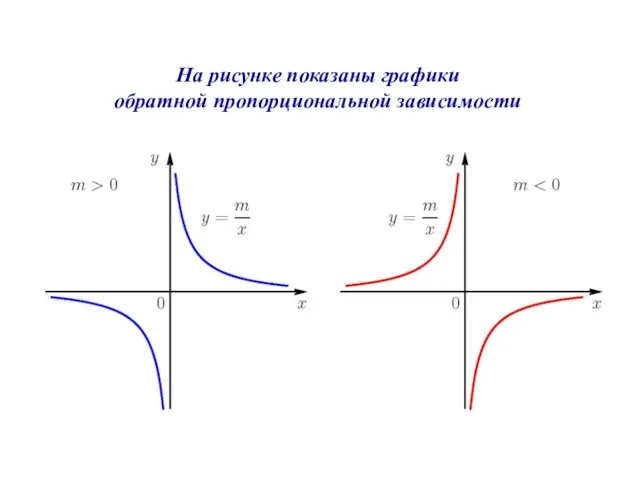
- 13. На рисунке показаны графики обратной пропорциональной зависимости
- 14. Отметим свойства функции в случае т > 0. 1. Функция определена для всех действительных чисел, кроме
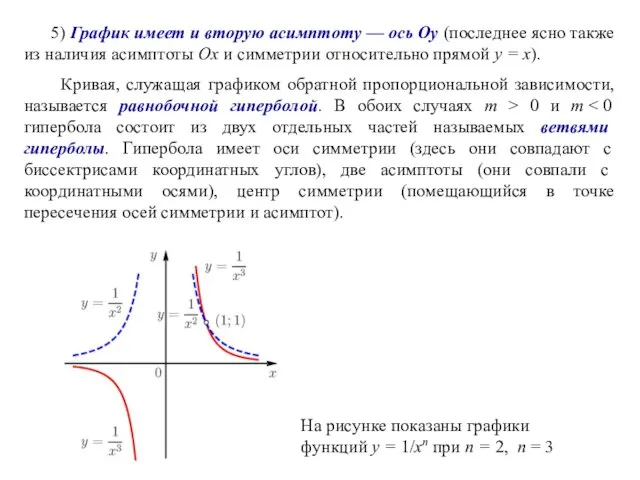
- 15. 5) График имеет и вторую асимптоту — ось Оу (последнее ясно также из наличия асимптоты Ох
- 16. Показательная функция Функция вида у = ах, при а > 0, а ≠ 1 называется показательной
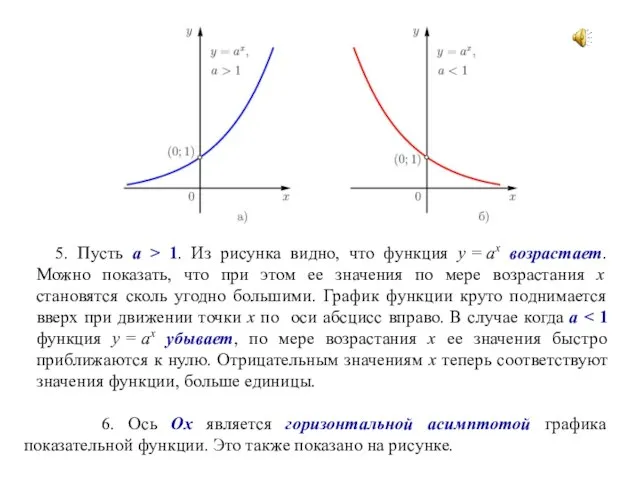
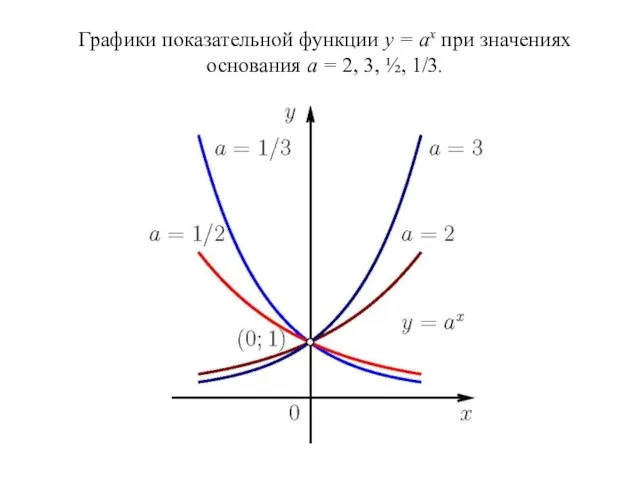
- 17. 5. Пусть а > 1. Из рисунка видно, что функция у = ах возрастает. Можно показать,
- 18. Графики показательной функции у = ах при значениях основания а = 2, 3, ½, 1/3.
- 19. Логарифмическая функция Функция вида y = logax, где а > 0 и a ≠ 1, называется
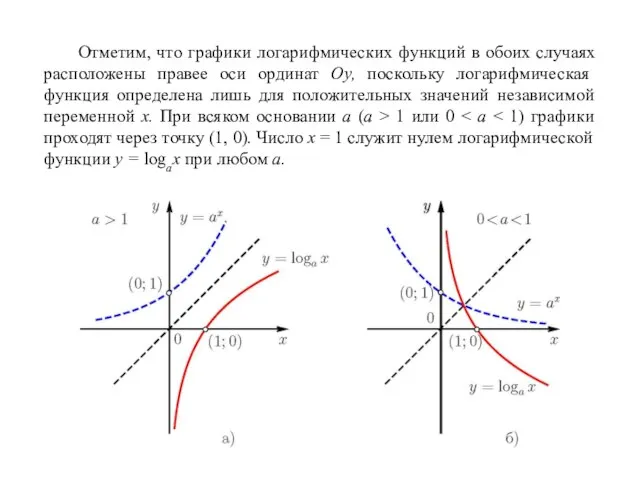
- 20. Отметим, что графики логарифмических функций в обоих случаях расположены правее оси ординат Оу, поскольку логарифмическая функция
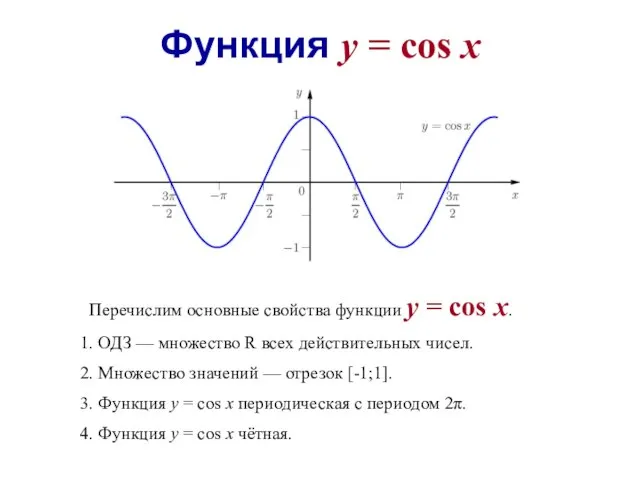
- 21. Функция y = cos x Перечислим основные свойства функции y = cos x. . ОДЗ —
- 22. 5. Функция y = cos x принимает: – значение, равное 0, при n∈Z; – наибольшее значение,
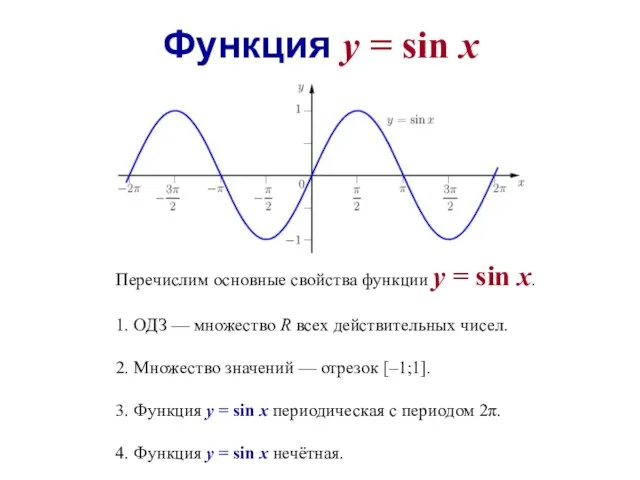
- 23. Функция y = sin x Перечислим основные свойства функции y = sin x. 1. ОДЗ —
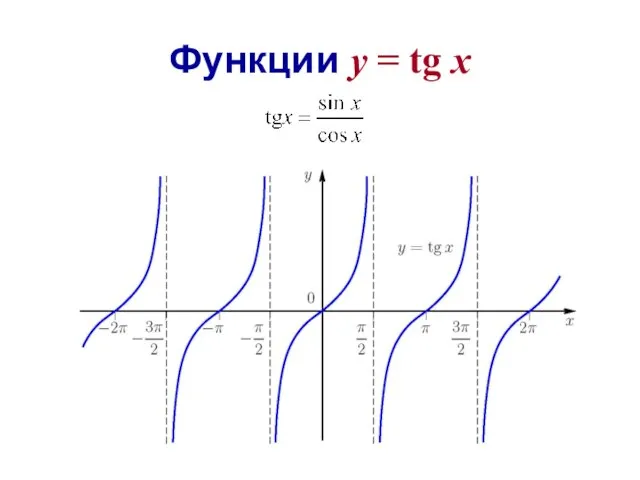
- 25. Функции y = tg x
- 26. Область определения функции - множество всех действительных чисел n∈Z. 2. Множество значений — множество R всех
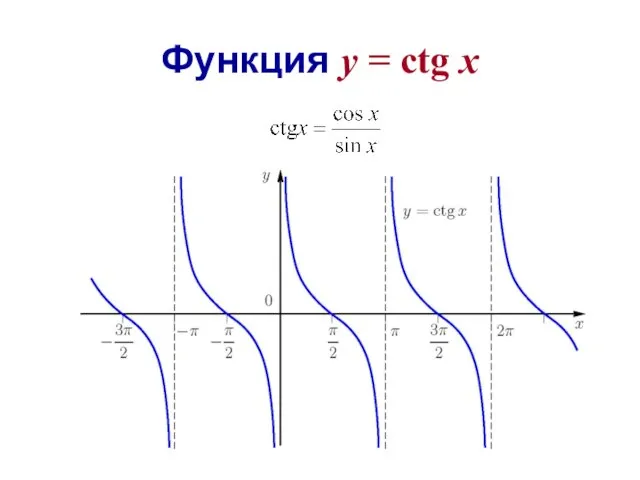
- 27. Функция y = сtg x
- 29. Скачать презентацию












 Сложение и вычитание десятичных дробей. 5 класс
Сложение и вычитание десятичных дробей. 5 класс Тренажёр Функция обратной пропорциональности
Тренажёр Функция обратной пропорциональности Тема: «Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых»
Тема: «Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых»  Презентация по математике "Сложение и вычитание дробей с разными знаменателями" - скачать бесплатно
Презентация по математике "Сложение и вычитание дробей с разными знаменателями" - скачать бесплатно Разные доказательства теоремы Пифагора
Разные доказательства теоремы Пифагора Раскрытие скобок. 6 класс
Раскрытие скобок. 6 класс Алгоритм решения и успех на ЕГЭ
Алгоритм решения и успех на ЕГЭ Аттестационная работа. Лабораторно-графическая работа "График функции"
Аттестационная работа. Лабораторно-графическая работа "График функции" Решение задач № 6 ЕГЭ
Решение задач № 6 ЕГЭ Объём шара
Объём шара Первообразная. Неопределенный интеграл
Первообразная. Неопределенный интеграл Возникновение слова “процент”. Древний Рим
Возникновение слова “процент”. Древний Рим Математический КВН
Математический КВН Подготовка к ЕГЭ. Задание В7
Подготовка к ЕГЭ. Задание В7 Проектная работа на тему: Симметрия в нашей жизни Выполнила: ученица 10А класса средней школы №8 Гизутдинова Диляра
Проектная работа на тему: Симметрия в нашей жизни Выполнила: ученица 10А класса средней школы №8 Гизутдинова Диляра  Какой я человек. Интеллектуальная разминка
Какой я человек. Интеллектуальная разминка Формулы. Урок изучения нового материала
Формулы. Урок изучения нового материала Математика в моей будущей профессии
Математика в моей будущей профессии Фракталы. Понятия фрактал и фрактальная геометрия
Фракталы. Понятия фрактал и фрактальная геометрия Тайна чисел. Числовые суеверия.
Тайна чисел. Числовые суеверия. Задания с производной при подготовке к ЕГЭ
Задания с производной при подготовке к ЕГЭ Уравнение Х2= a
Уравнение Х2= a Числовые последовательности. 9 класс
Числовые последовательности. 9 класс Арифметикалық прогрессияның анықтамасы, 9 сынып. Алгебра
Арифметикалық прогрессияның анықтамасы, 9 сынып. Алгебра Приемы быстрого счета без калькулятора
Приемы быстрого счета без калькулятора Аттестационная работа. Решение задач повышенной сложности
Аттестационная работа. Решение задач повышенной сложности Определение и основные свойства множеств
Определение и основные свойства множеств Понятия НОД и НОК,
Понятия НОД и НОК,