Содержание
- 2. Средняя длина кодового слова длина кодового слова
- 5. Теорема Крафта. Если – длины кодовых слов, соответствующих сообщениям , то необходимым и достаточным условием существования
- 6. Теорема Шеннона. При кодировании сообщений в алфавите насчитывающем m символов, при условии отсутствия шумов, средняя длина
- 7. ДИСКРЕТНЫЕ КАНАЛЫ С ШУМАМИ Модель канала связи при наличии шумов
- 9. Пропускная способность дискретного канала связи с шумами
- 10. {Z} {Y}
- 11. H(Z) – априорная (безусловная) энтропия ансамбля {Z} энтропия ансамбля {Z}, оставшаяся после получения сообщения об ансамбле
- 13. Теоремы о кодировании в присутствие шумов
- 14. Теорема 1 (К. Шеннон). Если поток информации создаваемый источником где может быть сколь угодно малым положительным
- 15. Теорема 2 (К. Шеннон). Если поток информации создаваемый источником где , то среди кодов, обеспечивающих сколь
- 16. Теорема 3 (К. Шеннон). Если поток информации создаваемый источником где то никакой код не может сделать
- 17. Фундаментальное свойство энтропии дискретных эргодических источников
- 18. Теорема 1. Для любых ε>0 и δ>0 можно найти такое М0, при котором эргодические последовательности С
- 19. Следствие 1. Типичные последовательности приблизительно равновероятны и число их равно Следствие 2. При больших М множество
- 20. Следствие 3. Чтобы экспериментально определить энтропию эргодического источника, у которого вероятностные связи распространяются на очень большое
- 21. Пример 1. Эргодический источник с энтропией (бит) вырабатывает четыре различных символа. Найти отношение числа типичных к
- 22. Таким образом, типичные составляют одну тысячную всех возможных последовательностей.
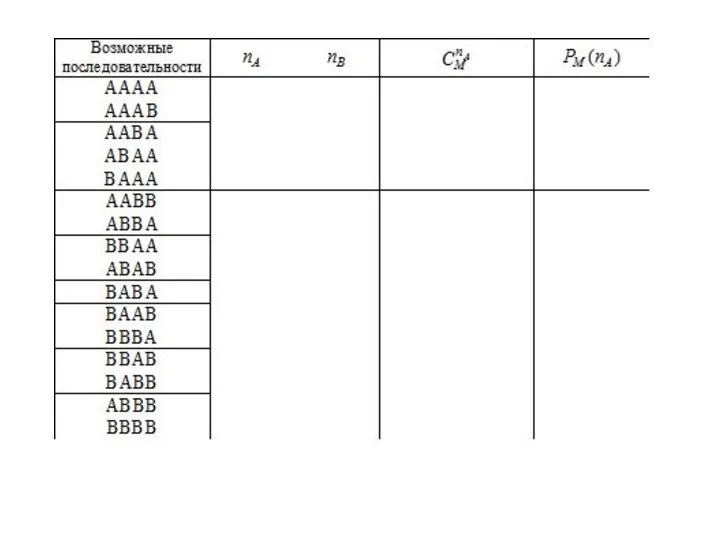
- 23. Пример 2. Источник вырабатывает с одинаковой вероятностью два символа А и В. Определить количество возможных последовательностей,
- 24. I случай. Пусть
- 26. II случай. Пусть
- 28. Скачать презентацию






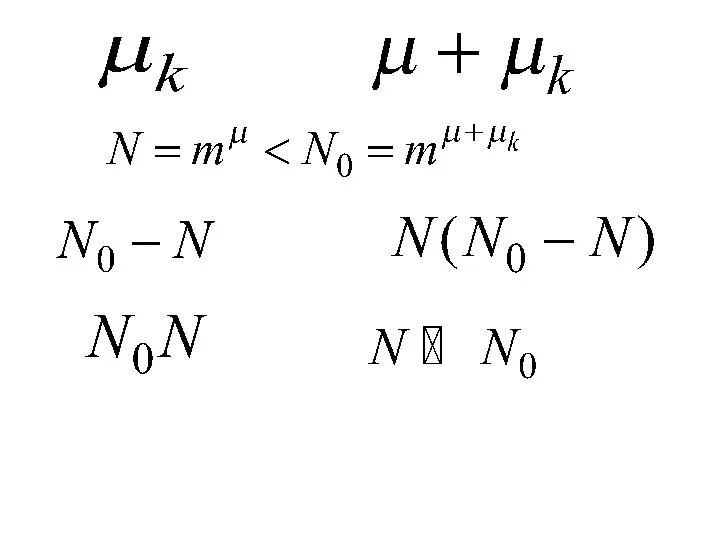

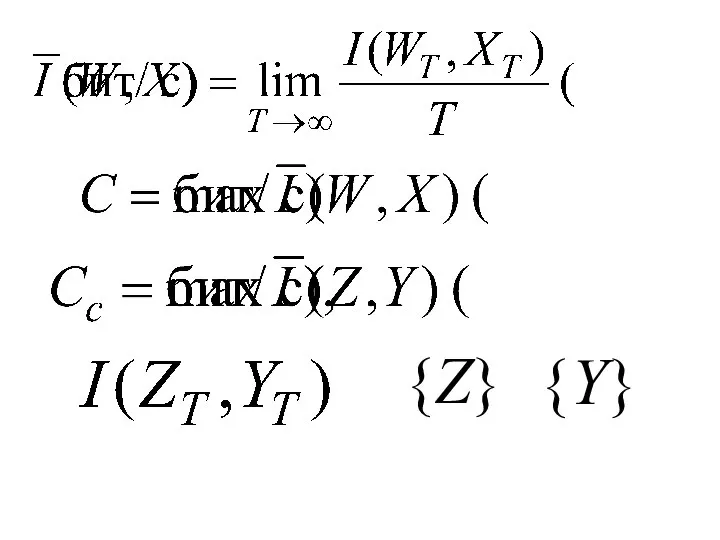

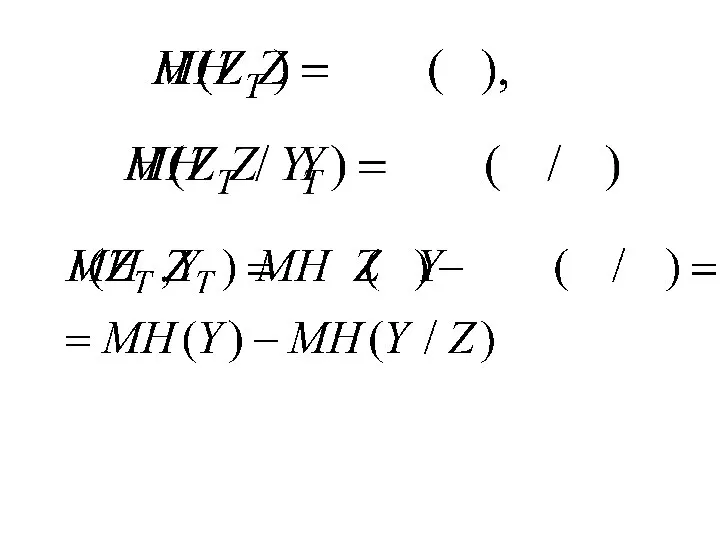











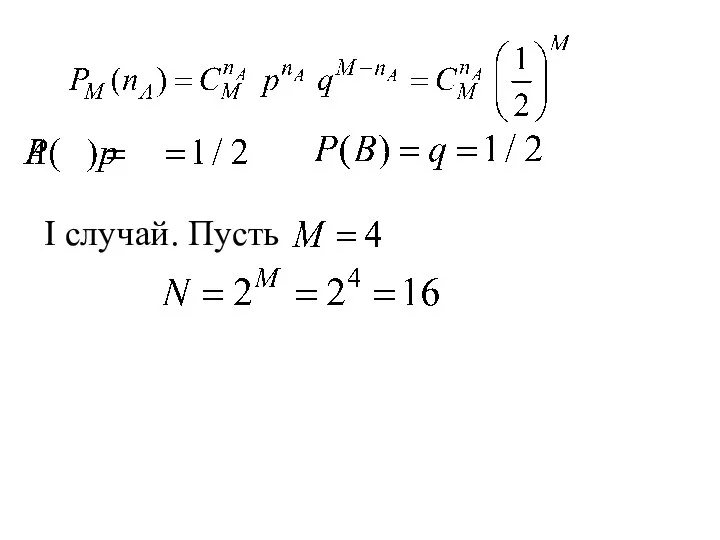

 Операции, функции, выражения
Операции, функции, выражения Открытый урок математики в 5 классе с использованием информационных технологий по теме «Задачи на части» Туктаровой Наили Миниб
Открытый урок математики в 5 классе с использованием информационных технологий по теме «Задачи на части» Туктаровой Наили Миниб Третий признак равенства треугольников
Третий признак равенства треугольников Законы распределения - I
Законы распределения - I Двугранный угол. Задания для устного счета. Упражнение 8
Двугранный угол. Задания для устного счета. Упражнение 8 Векторы в пространстве
Векторы в пространстве Масштаб
Масштаб Арифметическая прогрессия. Обобщающий урок
Арифметическая прогрессия. Обобщающий урок Лента Мёбиуса
Лента Мёбиуса Первый признак равенства треугольников
Первый признак равенства треугольников Математика для малышей
Математика для малышей Презентация по геометрии. Смежные и вертикальные. Перпендикулярные прямые. (7 класс)
Презентация по геометрии. Смежные и вертикальные. Перпендикулярные прямые. (7 класс) ЕГЭ Профиль. Решение задания №8
ЕГЭ Профиль. Решение задания №8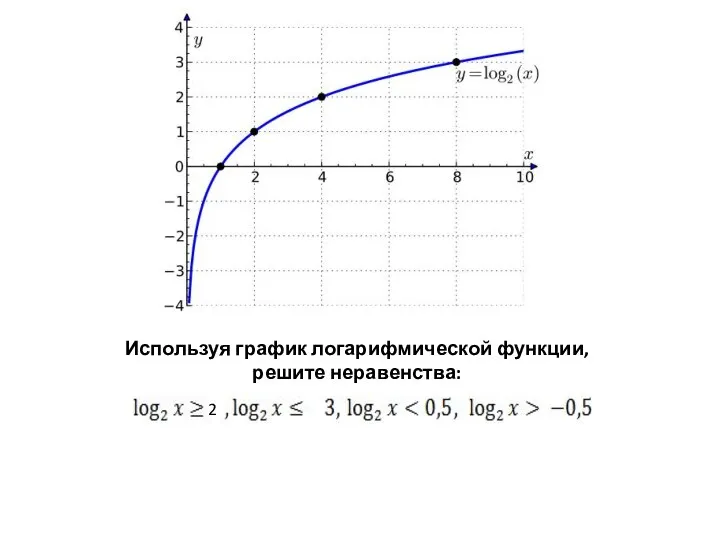 Логарифмические неравенства. устные упражнения
Логарифмические неравенства. устные упражнения Решение неравенств с одной переменной
Решение неравенств с одной переменной Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Нефть. Добыча, переработка, использование. Задачи на нахождение объёма цилиндра. Работа с формулами в таблице Excel
Нефть. Добыча, переработка, использование. Задачи на нахождение объёма цилиндра. Работа с формулами в таблице Excel Методы простых средних и скользящих средних
Методы простых средних и скользящих средних «Действия с десятичными дробями» Урок – путешествие 5 класс
«Действия с десятичными дробями» Урок – путешествие 5 класс Аттестационная работа. Программа курса внеурочной деятельности «Занимательная математика»
Аттестационная работа. Программа курса внеурочной деятельности «Занимательная математика» Операции комбинаторики
Операции комбинаторики Комбинаторика
Комбинаторика Аттестационная работа. Золотое сечение
Аттестационная работа. Золотое сечение Окружность, круг, их элементы и части. Центральный угол
Окружность, круг, их элементы и части. Центральный угол Расположение элементарных функций в ряд Маклорена. (Тема 14.4)
Расположение элементарных функций в ряд Маклорена. (Тема 14.4) Потенциальная яма в импульсном представлении
Потенциальная яма в импульсном представлении Логарифм. Основные свойства логарифмов
Логарифм. Основные свойства логарифмов Умножение одночленов
Умножение одночленов