Метод последовательной верхней релаксации (SOR)
x0=[0;0;0]
n=45
eps=0.00001
F=A'*A
H=A'*b
w=1.4
начало
for i=1:length(b)
for
newa(i,j)=0
beta(i)=H(i)/F(i,i)
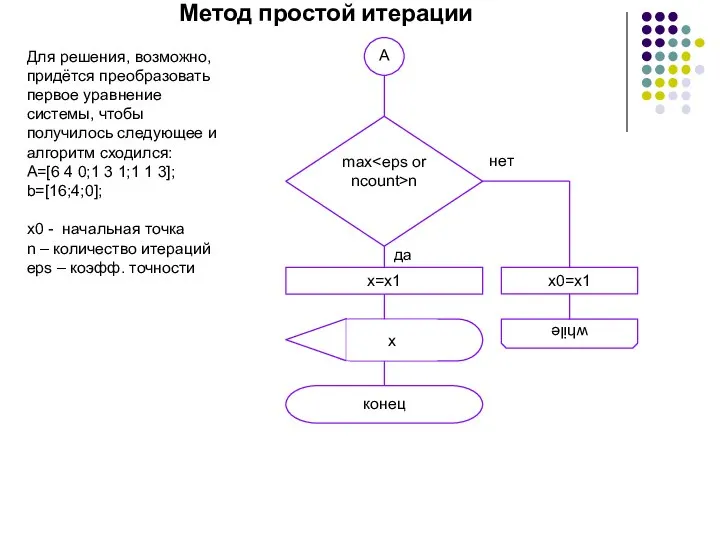
A=[1 1 1;1 3 1;1
1 3];
b=[2;4;0];
x0 - начальная точка
n – количество итераций
eps – коэфф. точности
w – коэфф. релаксации
выделенный цветом прямоугольник – единственное отличие от предыдущего метода
Заметьте, что в этом методе достаточно всего 45 итераций
for j=1:length(b)
i==j
да
нет
newa(i,j)=-F(i,j)/F(i,i)
for
x1=x0
ncount=0
beta=beta'
while true
ncount=ncount+1
for j=1:length(b)
for
C
for i=1:length(b)
s=0
s=s+newa(i,j)*x1(j)
for
max=|x0(1)-x1(1)|
x1(i)=beta(i)+s+(w-1)*(beta(i)+s-x0(i))


![Итерационный метод Ричардсона tau=0.1 x=[0;0;0] n=250 начало for i=1:n for r=b-A*x](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/691462/slide-3.jpg)
![Метод простой итерации x0=[0;0;0] n=2000 eps=0.0001 начало for i=1:length(b) for newa(i,j)=0](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/691462/slide-4.jpg)
![Метод Гаусса-Зейделя x0=[0;0;0] n=2000 eps=0.0001 F=A'*A H=A'*b начало for i=1:length(b) for](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/691462/slide-6.jpg)
![Метод Гаусса-Зейделя конец A=[1 1 1;1 3 1;1 1 3]; b=[2;4;0];](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/691462/slide-7.jpg)
![Метод последовательной верхней релаксации (SOR) x0=[0;0;0] n=45 eps=0.00001 F=A'*A H=A'*b w=1.4](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/691462/slide-8.jpg)
 Двухфакторный дисперсионный анализ
Двухфакторный дисперсионный анализ Методы математического программирования при автоматизации конструирования ЭА
Методы математического программирования при автоматизации конструирования ЭА Презентация по математике "Показательная функция, её свойства и график" - скачать
Презентация по математике "Показательная функция, её свойства и график" - скачать  Исследовательские задания для учащихся на уроках математики
Исследовательские задания для учащихся на уроках математики  Мир геометрии
Мир геометрии Преемственность в формировании универсальных учебных действий и личностных результатов
Преемственность в формировании универсальных учебных действий и личностных результатов Формула полной вероятности
Формула полной вероятности Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Решение неравенств
Решение неравенств Город Салават, Республика Башкортостан. Региональный компонент на уроках математики в начальных классах
Город Салават, Республика Башкортостан. Региональный компонент на уроках математики в начальных классах Расчет геометрических параметров объекта
Расчет геометрических параметров объекта Математический анализ
Математический анализ Урок геометрии в 8 классе. Обобщение темы: «Четырехугольники»
Урок геометрии в 8 классе. Обобщение темы: «Четырехугольники» Неравные функции
Неравные функции Перпендикулярные прямые
Перпендикулярные прямые Аналитическая геометрия. Прямая на плоскости
Аналитическая геометрия. Прямая на плоскости Квадратичная функция и её свойства
Квадратичная функция и её свойства Знаки тригонометрических функций
Знаки тригонометрических функций Компьютерное моделирование физических процессов, как средство формирования математических понятий
Компьютерное моделирование физических процессов, как средство формирования математических понятий Уравнения, приводимые к квадратным. Урок для 9 класса
Уравнения, приводимые к квадратным. Урок для 9 класса Решение задач на проценты
Решение задач на проценты Матрицы и определители
Матрицы и определители Синус, косинус и тангенс
Синус, косинус и тангенс Предел и непрерывность функции
Предел и непрерывность функции Специальные распределения. χ2 -распределение
Специальные распределения. χ2 -распределение Задачка по математике Прогулка
Задачка по математике Прогулка Некоторые другие приемы сравнения дробей
Некоторые другие приемы сравнения дробей Лінійка — найпростіший прилад для вимірювання довжини
Лінійка — найпростіший прилад для вимірювання довжини