Содержание
- 2. 1. Понятие группы преобразований
- 3. Умножение преобразований Некоторые преобразования можно составить из нескольких других.
- 4. Умножение преобразований Некоторые преобразования можно составить из нескольких других. Пример. Винтовые движения составляются из поворотов вокруг
- 5. Умножение преобразований Некоторые преобразования можно составить из нескольких других. Пример. Винтовые движения составляются из поворотов вокруг
- 6. Пусть есть некоторая совокупность преобразований с операцией умножения. Она обладает такими свойствами:
- 7. Пусть есть некоторая совокупность преобразований с операцией умножения. Она обладает такими свойствами: 1. Произведение двух преобразований,
- 8. Пусть есть некоторая совокупность преобразований с операцией умножения. Она обладает такими свойствами: 1. Произведение двух преобразований,
- 9. Пусть есть некоторая совокупность преобразований с операцией умножения. Она обладает такими свойствами: 1. Произведение двух преобразований,
- 10. Пусть есть некоторая совокупность преобразований с операцией умножения. Она обладает такими свойствами: 1. Произведение двух преобразований,
- 11. Таким образом, всякая совокупность взаимно однозначных преобразований множества М, обладающая этими свойствами, называется группой преобразований множества
- 12. Таким образом, всякая совокупность взаимно однозначных преобразований множества М, обладающая этими свойствами, называется группой преобразований множества
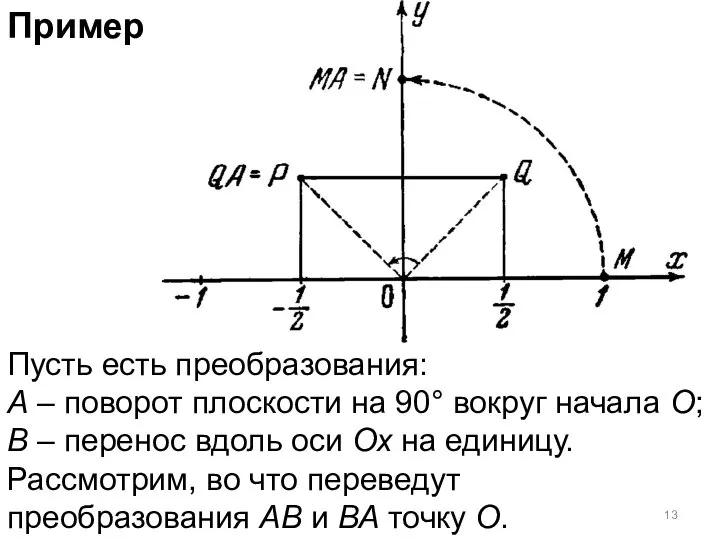
- 13. Пример Пусть есть преобразования: А – поворот плоскости на 90° вокруг начала О; В – перенос
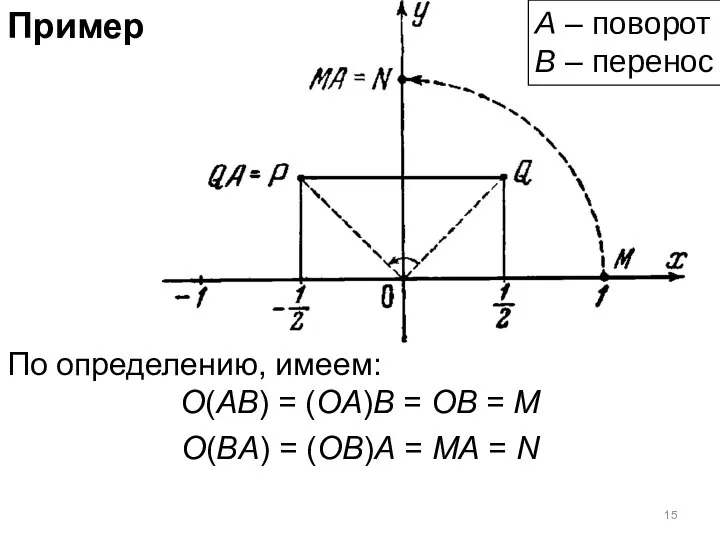
- 14. Пример По определению, имеем: O(AB) = (OA)B = OB = M А – поворот В –
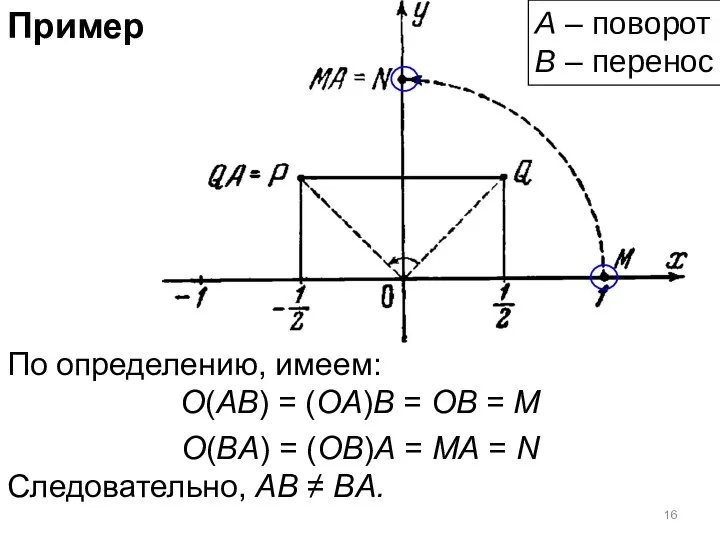
- 15. Пример По определению, имеем: O(AB) = (OA)B = OB = M O(BA) = (OB)A = MA
- 16. Пример По определению, имеем: O(AB) = (OA)B = OB = M O(BA) = (OB)A = MA
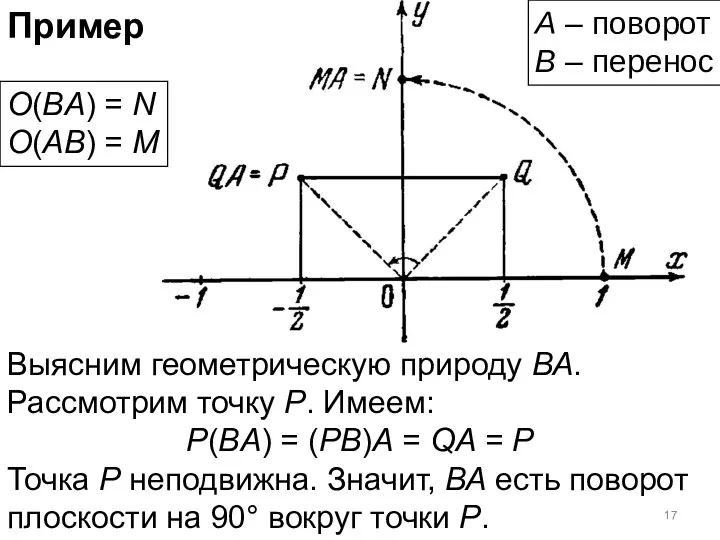
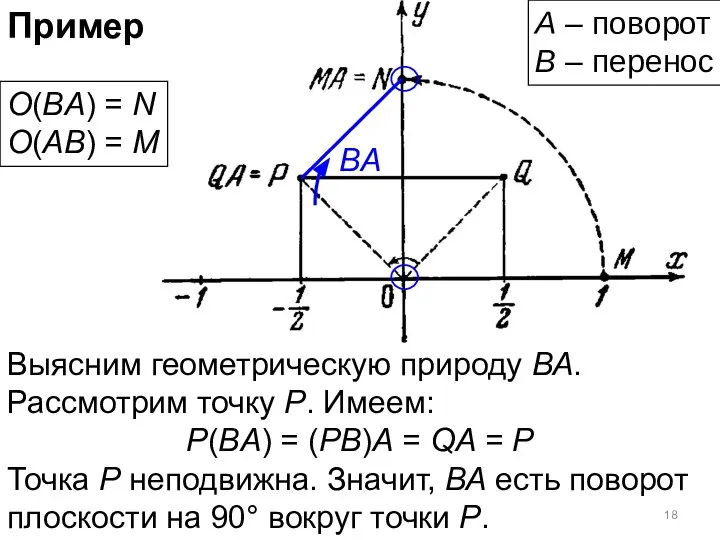
- 17. Пример Выясним геометрическую природу ВА. Рассмотрим точку Р. Имеем: P(BA) = (PB)A = QA = P
- 18. Пример Выясним геометрическую природу ВА. Рассмотрим точку Р. Имеем: P(BA) = (PB)A = QA = P
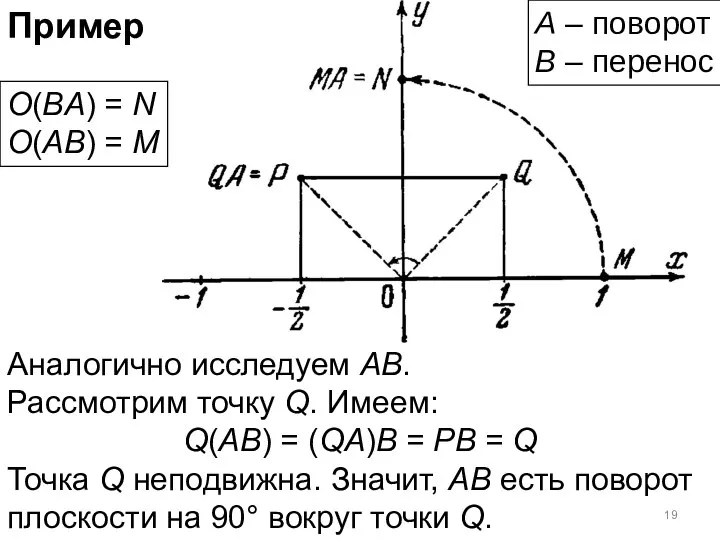
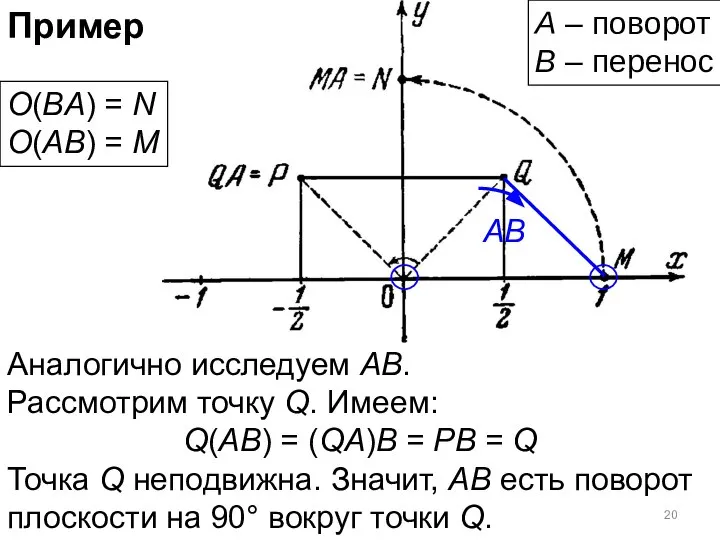
- 19. Пример Аналогично исследуем АВ. Рассмотрим точку Q. Имеем: Q(AB) = (QA)B = PB = Q Точка
- 20. Пример Аналогично исследуем АВ. Рассмотрим точку Q. Имеем: Q(AB) = (QA)B = PB = Q Точка
- 21. 2. Группа проективных преобразований
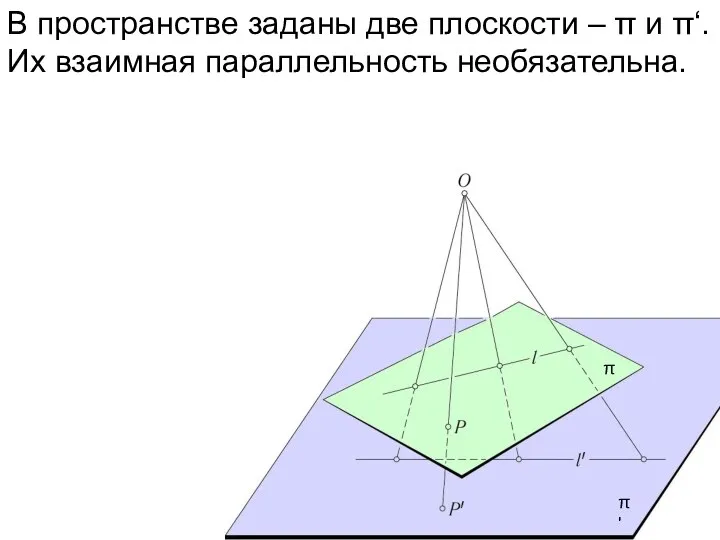
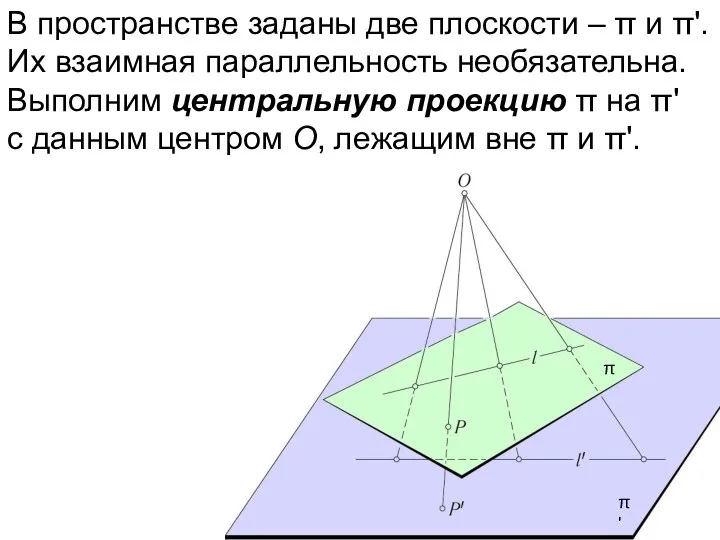
- 22. В пространстве заданы две плоскости – π и π‘. Их взаимная параллельность необязательна. π π'
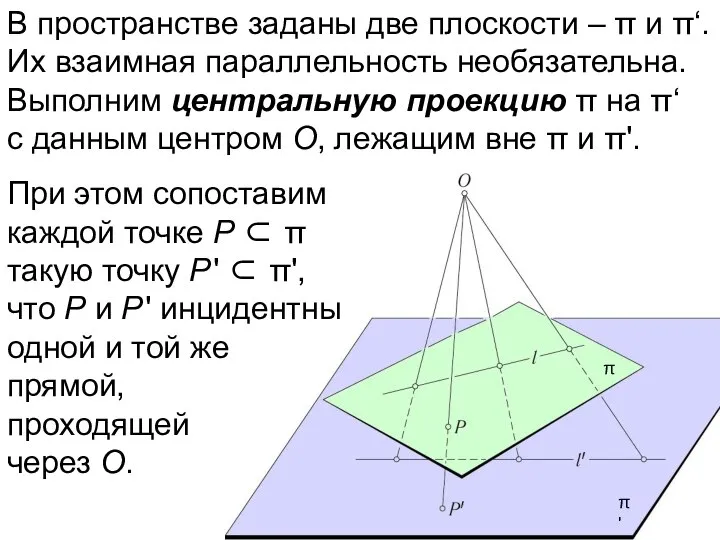
- 23. В пространстве заданы две плоскости – π и π'. Их взаимная параллельность необязательна. Выполним центральную проекцию
- 24. В пространстве заданы две плоскости – π и π‘. Их взаимная параллельность необязательна. Выполним центральную проекцию
- 25. Аналогично выполняем подобным же образом параллельную проекцию. При этом предполагаем, что проектирующие прямые параллельны между собой.
- 26. Точно так же определяется проекция прямой или кривой линии l в плоскости π на некоторую линию
- 27. Всякое отображение одной фигуры на другую, которое получается посредством проектирования (центрального или параллельного) или же посредством
- 28. Замечание Если две фигуры связаны только одним проектированием, то говорят, что они перспективны.
- 29. Замечание Если две фигуры связаны только одним проектированием, то говорят, что они перспективны. Таким образом, если
- 30. Замечание Если две фигуры связаны только одним проектированием, то говорят, что они перспективны. Таким образом, если
- 31. Проективная геометрия плоскости или прямой составляется из системы геометрических теорем, сохраняющихся при произвольных проективных преобразованиях соответствующих
- 32. Проективной геометрии противопоставляется метрическая геометрия, которая понимается как система теорем, устанавливающих связи между величинами в рассматриваемых
- 33. Cформулируем некоторые проективные свойства.
- 34. Точка проектируется в точку.
- 35. Точка проектируется в точку. Прямая линия проектируется в прямую.
- 36. Точка проектируется в точку. Прямая линия проектируется в прямую. Покажем это.
- 37. π π' Точка проектируется в точку. Прямая линия проектируется в прямую. Покажем это. Если прямая l
- 38. Если точка A и прямая l инцидентны, то точка A' и прямая l', возникающие из них
- 39. Если точка A и прямая l инцидентны, то точка A' и прямая l', возникающие из них
- 40. Следствия.
- 41. Если три точки (или более) коллинеарны, т.е. инцидентны с одной и той же прямой, то их
- 42. Если три точки (или более) коллинеарны, т.е. инцидентны с одной и той же прямой, то их
- 43. Если три точки (или более) коллинеарны, т.е. инцидентны с одной и той же прямой, то их
- 44. Итак, инцидентность, коллинеарность, конкуррентность являются проективными свойствами (инвариантными относительно проективных преобразований).
- 45. Итак, инцидентность, коллинеарность, конкуррентность являются проективными свойствами (инвариантными относительно проективных преобразований). Величины отрезков и углов, а
- 46. Пример
- 47. Равнобедренные или равносторонние треугольники могут спроектироваться на треугольники с тремя различными сторонами.
- 49. Скачать презентацию




































 Целые числа. Рациональные числа
Целые числа. Рациональные числа Cредняя линия треугольника, средняя линия трапеции
Cредняя линия треугольника, средняя линия трапеции Двойные интегралы
Двойные интегралы Вписанная и описанная окружности
Вписанная и описанная окружности Приведенные квадратные уравнения
Приведенные квадратные уравнения Оптимальная математика Презентация учащихся 11 класса Седых П. Комкова В. Склейнова А._
Оптимальная математика Презентация учащихся 11 класса Седых П. Комкова В. Склейнова А._ Системы линейных уравнений. Матрицы
Системы линейных уравнений. Матрицы Формирование навыков УУД при изучении темы «Решение задач на построение графиков алгебраических функций» (на примере линейно
Формирование навыков УУД при изучении темы «Решение задач на построение графиков алгебраических функций» (на примере линейно Действия с обыкновенными дробями. Создание открытого акционерного общества
Действия с обыкновенными дробями. Создание открытого акционерного общества Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Математизация научных исследований в исторической науке
Математизация научных исследований в исторической науке Координаты на плоскости (открытый урок, 6 класс)
Координаты на плоскости (открытый урок, 6 класс) Геометрический смысл двойного интеграла
Геометрический смысл двойного интеграла Методы решения уравнений
Методы решения уравнений Применение теории вероятностей в анализе спортивных событий
Применение теории вероятностей в анализе спортивных событий Графики функций1. Готовимся к ОГЭ
Графики функций1. Готовимся к ОГЭ Числа и выражения (9 класс)
Числа и выражения (9 класс) Законы и правила математической логики. Упрощение сложных высказываний
Законы и правила математической логики. Упрощение сложных высказываний Действия с отрицательными и положительными числами на уроках математики и географии
Действия с отрицательными и положительными числами на уроках математики и географии Масштаб. Урок математики в 6 классе
Масштаб. Урок математики в 6 классе Кері байланыс
Кері байланыс Свойства функций. Область определения функции
Свойства функций. Область определения функции Методы решения иррациональных уравнений. (10 класс)
Методы решения иррациональных уравнений. (10 класс) Окружность и её элементы
Окружность и её элементы Учимся решать задачи с помощью уравнения
Учимся решать задачи с помощью уравнения Задачи на увеличение и уменьшение числа на несколько единиц
Задачи на увеличение и уменьшение числа на несколько единиц Многогранники. Все формулы. Геометрия (10-11 класс)
Многогранники. Все формулы. Геометрия (10-11 класс) Уравнения. Назвать уравнения
Уравнения. Назвать уравнения