Содержание
- 2. Линейные дифференциальные уравнения 1-го порядка. Уравнение Бернулли. Дифференциальное уравнение вида (1) относительно называется линейным. y’+P(x)y=Q(x) y,y’
- 3. Для этого подставляем в уравнение (1) определяемые из (3), и из полученного дифференциального уравнения определяем функцию
- 4. Уравнение Бернулли Уравнение 1-го порядка вида , где , называется уравнением Бернулли. Оно приводится к линейному
- 5. Первое уравнение – уравнение с разделяющимися переменными: Следовательно, Решить уравнение Решение. Соответствующее однородное уравнение есть .
- 6. Решить уравнение Решение. Это – уравнение Бернулли Полагаем y=uv, получим: (*) Для определения функции u потребуем
- 7. Решить уравнение Решение. Это – уравнение Бернулли. Проинтегрируем его методом вариации произвольной постоянной. Для этого интегрируем
- 9. Скачать презентацию






 Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Деление обыкновенных дробей
Деление обыкновенных дробей Математические головоломки
Математические головоломки Асимптоты графика функции
Асимптоты графика функции Математика 5 класс. Тренировочный тест № 1
Математика 5 класс. Тренировочный тест № 1 Вычисление пределов функции. Предел функции на бесконечности. Два замечательных предела. Вычисление числа «е»
Вычисление пределов функции. Предел функции на бесконечности. Два замечательных предела. Вычисление числа «е» Деление дробей (6 класс) - Презентация по математике_
Деление дробей (6 класс) - Презентация по математике_ Постановка задачи оптимизации (основные этапы и пример)
Постановка задачи оптимизации (основные этапы и пример) Скачать презентацию Острова Атлантического океана БЕРМУДЫ
Скачать презентацию Острова Атлантического океана БЕРМУДЫ  Число и цифра 1
Число и цифра 1 Решение заданий В5 по математике. ЕГЭ
Решение заданий В5 по математике. ЕГЭ Контент-анализ на тему: «Компаративный анализ популярных новогодних сказок в России»
Контент-анализ на тему: «Компаративный анализ популярных новогодних сказок в России» Сечения многогранника (задачи)
Сечения многогранника (задачи)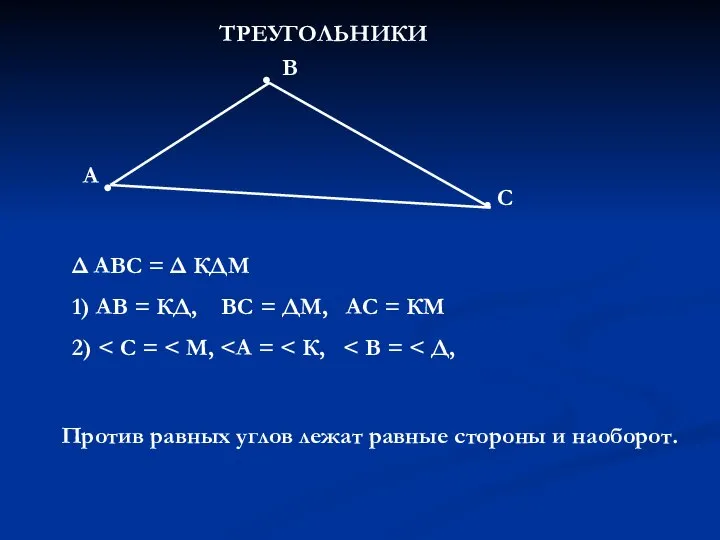 Первый признак равенства треугольников. Задачи
Первый признак равенства треугольников. Задачи Осевая симметрия
Осевая симметрия Равенство треугольников. Второй признак равенства треугольников
Равенство треугольников. Второй признак равенства треугольников Презентация по математике "Конкурс «А, ну-ка, девочки» по математике для учащихся 7 класса" - скачать
Презентация по математике "Конкурс «А, ну-ка, девочки» по математике для учащихся 7 класса" - скачать  Многогранник. Призма
Многогранник. Призма Презентация по математике "«Задачи на движение» 4 класс" - скачать бесплатно
Презентация по математике "«Задачи на движение» 4 класс" - скачать бесплатно Правильные многогранники
Правильные многогранники Задачи на переливание жидкости
Задачи на переливание жидкости Геометрическое место точек
Геометрическое место точек Сумма углов треугольника
Сумма углов треугольника Сумма углов треугольника
Сумма углов треугольника Композиция функций (сложная функция)
Композиция функций (сложная функция) Вычисление площадей на квадратной решетке
Вычисление площадей на квадратной решетке Сумма и разность синусов и косинусов
Сумма и разность синусов и косинусов Площади круга
Площади круга