Содержание
- 2. План Основы статистического описания. Гистограмма и полигон частот. Эмпирическое распределение и его свойства
- 3. Основы статистического описания Математическая статистика используется в различных областях знаний: в экономике, опытном деле, земледелии, животноводстве
- 4. Математическая статистика §1. Предмет и задачи математической статистики. Определение 1. Математическая статистика – это наука, занимающаяся
- 5. Математическая статистика Результаты измерений (наблюдений) называют статистическими данными. В зависимости от поставленной цели все задачи математической
- 6. Математическая статистика Определение 2. Вся исследуемая совокупность однородных объектов называется генеральной совокупностью. Если предположить, что над
- 7. Математическая статистика Как и в теории вероятностей, вероятность для всех значений Х в генеральной совокупности, меньших
- 8. Математическая статистика Определение 3. Множество из n- объектов, отоб-ранных случайным образом из генеральной совокупности, называется выборочной
- 9. Математическая статистика Определение 4. Метод, основанный на том, что по данным обследования выборки, выделенной из данной
- 10. Математическая статистика В реальных социально - экономических системах нельзя проводить эксперименты, поэтому данные обычно представляют собой
- 11. Математическая статистика Вариационные ряды. Определение 1. Значение случайной величины, соответствующее отдельной группе сгруппи-рованного ряда наблюдаемых данных,
- 12. Математическая статистика Вариационные ряды. Определение 2. Вариационным рядом называется ранжирование в порядке возрастания вариант с соответствующими
- 13. Математическая статистика Для каждой группы сгруппированного ряда данных можно подсчитать их численность, т.е. определить число, которое
- 14. Математическая статистика Определение 5. Отношение частоты данного варианта к объему совокупности называется относительной частотой или частостью
- 15. Математическая статистика Частость является статистической вероят-ностью появления варианта xi . Она обладает свойством устойчивости, или, иначе,
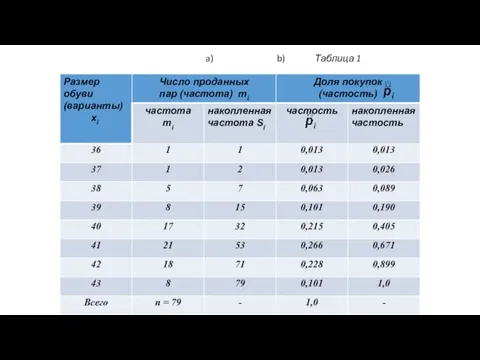
- 16. Математическая статистика Пример 1: Пусть мы интересуемся размерами проданной в магазине мужской обуви за некоторый отрезок
- 17. Математическая статистика Интересующий нас признак принимает различные и притом только целые значения, причем он постоянно меняется,
- 18. a) b) Таблица 1
- 19. Математическая статистика Получен вариационный ряд. Он может быть записан с указанием числа проданных пар (частот каждого
- 20. Математическая статистика Определение 6. Дискретным вариационным рядом распределения называется ранжированная сово-купность вариантов с соответствующими им частотами
- 21. Математическая статистика Определение 7. Накопленные частоты характери-зуют число членов данной совокупности, у которых рассматриваемый признак принимает
- 22. Математическая статистика Кроме дискретных вариационных рядов широкое применение имеют непрерывные (интервальные) вариационные ряды. Определение 9. Интервальным
- 23. Математическая статистика Интервальный ряд целесообразно построить, если число возможных значений дискретной величины велико или признак является
- 24. Математическая статистика Считая, что все частичные интервалы имеют одну и ту же длину, для каждого интервала
- 25. Математическая статистика Размах варьирования определяется по формуле: Для определения величины частичного интервала воспользуемся формулой Стерджесса: (*),
- 26. Математическая статистика Тогда формулу (*) можно записать: Если окажется, что h - дробное число, то за
- 27. Математическая статистика За начало первого интервала рекомендуется брать величину: Конец последнего интервала Хкон должен удов-летворять условию:
- 28. Математическая статистика Теперь, просматривая, результаты наблюдений, определяем, сколько значений признака попало в каждый конкретный интервал. При
- 29. Математическая статистика Границы полученной последовательности интервалов записывают в столбец, а затем, просматривая данные в том порядке,
- 30. Математическая статистика .
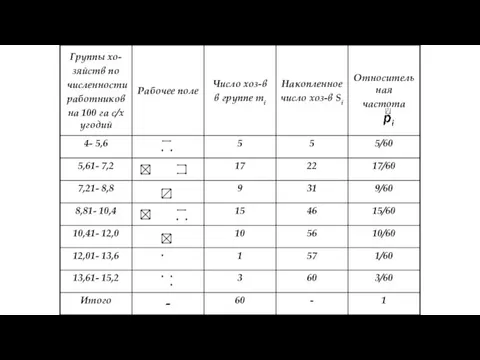
- 31. Математическая статистика Пример 2: Пусть дан ряд распределения хозяйств по количеству рабочих на 100 га с/х
- 32. Математическая статистика Решение. Для определения числа групп подставим значение n=60 в формулу Стерджесса: Найдем длину частичного
- 34. Математическая статистика Иногда интервальный вариационный ряд для простоты исследований условно заменяют дискретным. В этом случае серединное
- 35. Математическая статистика Графическое изображение вариационных рядов. Графическое изображение позволяет предста-вить в наглядной форме закономерности варьирования значений
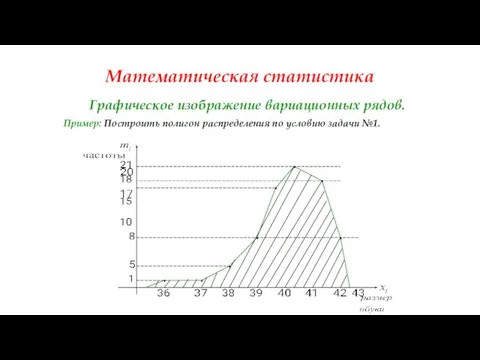
- 36. Математическая статистика Графическое изображение вариационных рядов. Пример: Построить полигон распределения по условию задачи №1.
- 37. Математическая статистика Графическое изображение вариационных рядов. Определение 2. Гистограммой (для интервального вариационного ряда) называют ступенчатую фи-гуру,
- 38. Математическая статистика Графическое изображение вариационных рядов. Пример: Построить гистограмму по данным примера 2.
- 39. Математическая статистика Графическое изображение вариационных рядов. Если в вариационном ряду вместо частот взяты соответственно накопленные частоты,
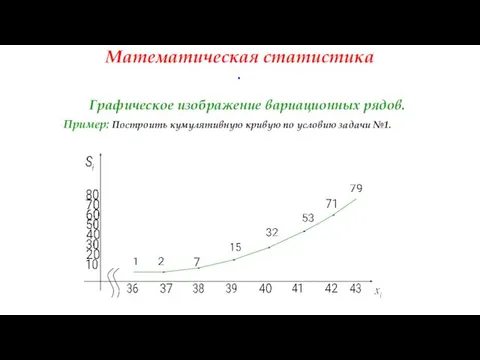
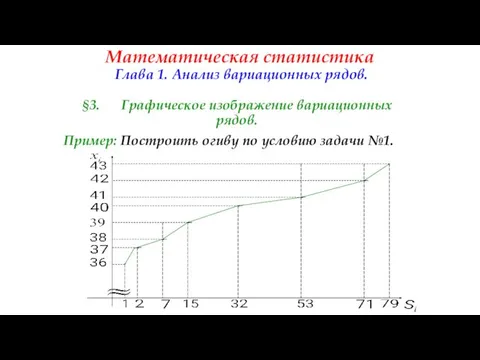
- 40. Математическая статистика . Графическое изображение вариационных рядов. Пример: Построить кумулятивную кривую по условию задачи №1.
- 41. Математическая статистика Графическое изображение вариационных рядов. Определение 4. Если по оси абсцисс откладывать накопленные частоты, а
- 42. Математическая статистика Глава 1. Анализ вариационных рядов. §3. Графическое изображение вариационных рядов. Пример: Построить огиву по
- 43. Математическая статистика Числовые характеристики вариационных рядов. Вариационные ряды позволяют получить первое представление об изучаемом распределении. Далее
- 44. Математическая статистика Числовые характеристики вариационных рядов. Определение 1. Средней арифметической дискретного вариационного ряда называется отношение суммы
- 45. Математическая статистика Числовые характеристики вариационных рядов. Пример: Найти по условию задачи 1. Вычисленное по формуле (1)
- 46. Математическая статистика Числовые характеристики вариационных рядов. Пример: Найти по условию задачи 2.
- 47. Математическая статистика Числовые характеристики вариационных рядов. Определение 2. Модой дискретного вари-ационного ряда называется вариант, имеющий наибольшую
- 48. Математическая статистика Числовые характеристики вариационных рядов. Пример: Найти по условию задачи 1. Для интервальных вариационных рядов
- 49. Математическая статистика Числовые характеристики вариационных рядов. ,где x0 - начало модального интервала; h - длина частичного
- 50. Математическая статистика Числовые характеристики вариационных рядов. Пример: Найти по условию задачи 2.
- 51. Математическая статистика Числовые характеристики вариационных рядов. Определение 3. Медианой дискретного вариационного ряда называется вариант, делящий ряд
- 52. Математическая статистика Числовые характеристики вариационных рядов. Если дискретный вариационный ряд имеет нечетное (2n-1) число значений варьирующего
- 53. Математическая статистика Числовые характеристики вариационных рядов. Пример: Найти по условию задачи 1.
- 54. Математическая статистика Числовые характеристики вариационных рядов. При нахождении для интервальных вариа-ционных рядов используют формулу: , где
- 55. Математическая статистика Числовые характеристики вариационных рядов. x0 - начало медианного интервала; h - длина частичного интервала;
- 56. Математическая статистика Числовые характеристики вариационных рядов. Пример: Найти по условию задачи 2. медиана расположена в интер-
- 57. Математическая статистика Числовые характеристики вариационных рядов. Определение 4. Дисперсия вариационного ряда (как дискретного, так и интервального)
- 58. Математическая статистика Числовые характеристики вариационных рядов. Определение 5. Среднее квадратическое откло-нение вариационного ряда распределения харак-теризует те
- 59. Математическая статистика Числовые характеристики вариационных рядов. Определение 6. Коэффициент вариации характе-ризует относительное значение среднего квад-ратического отклонения
- 60. Математическая статистика Числовые характеристики вариационных рядов. Соотношения между начальными и центральными моментами: Коэффициент асимметрии – Эксцесс
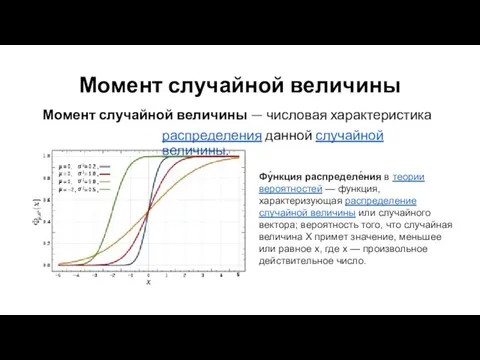
- 61. Момент случайной величины Момент случайной величины — числовая характеристика распределения данной случайной величины. Фу́нкция распределе́ния в
- 62. Математическая статистика Числовые характеристики вариационных рядов. Моменты для вариационных рядов в математи-ческой статистике находятся по формулам,
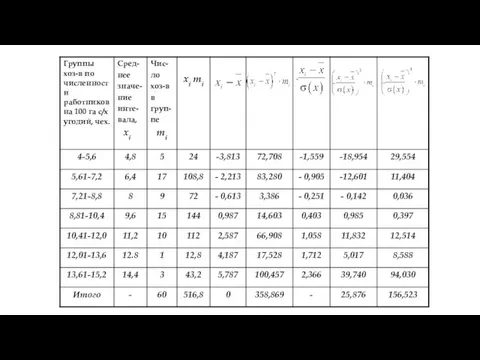
- 63. Математическая статистика Числовые характеристики вариационных рядов. Пример: Рассчитать дисперсию, среднее квад-ратическое отклонение, коэффициенты вариации, асимметрии и
- 65. Математическая статистика Глава 1. Анализ вариационных рядов. §4. Числовые характеристики вариационных рядов.
- 66. Математическая статистика Глава 1. Анализ вариационных рядов. §4. Числовые характеристики вариационных рядов. Таким образом, средняя численность
- 67. Математическая статистика Глава 1. Анализ вариационных рядов. §4. Числовые характеристики вариационных рядов.
- 68. Математическая статистика Глава 1. Анализ вариационных рядов. §4. Числовые характеристики вариационных рядов. Найденное значение коэффициента асим-метрии
- 69. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. В реальных условиях обычно бывает трудно
- 70. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Свойства (закон распределения и его парамет-ры)
- 71. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Различают 5 основных типов выборок: 1.
- 72. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. 2. Типическая – генеральная совокупность предварительно
- 73. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. б) пропорциональные (численность выборок формируют пропорционально
- 74. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. 3. Механическая – отбор элементов проводится
- 75. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. После осуществления выборки возникает задача оценки
- 76. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Пусть выборочная характеристика, вычисленная по результатам
- 77. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. 1) Состоятельность. Оценка является состо-ятельной оценкой
- 78. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. 2) Несмещенность. Оценка генеральной характеристики Θ
- 79. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. 3) Эффективность. Несмещенная оценка генеральной характеристики
- 80. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Статистики и являются состоятельны-ми, несмещенными и
- 81. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. На практике используют исправленную выбо-рочную дисперсию
- 82. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Кроме того, в расчетах используют стандартную
- 83. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Пусть точечная оценка параметра Θ. Чем
- 84. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. В качестве (1-) принимают значения 0,90;0,95;
- 85. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Точечная оценка вероятности pi определяется как
- 86. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. 1. для повторного отбора: Статистика u
- 87. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Отсюда: или , где Ф- функция
- 88. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. 2. Для бесповторного отбора: Доверительный интервал
- 89. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Предельная ошибка выборки: , где t
- 90. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Определение 3. Квантилем или нормированным отклонением
- 91. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Существуют таблицы значений для t в
- 92. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Пример: По условию задачи 2. При
- 93. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Решение. 1) Несмещенной оценкой M(x) является
- 94. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. 2) Средняя численность работников на 100
- 95. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Учитывая, что проводилась 10% выборка, N=10·
- 96. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. 3) Необходимый объем выборки, для того,
- 97. Математическая статистика Глава 1. Анализ вариационных рядов. §5. Выборочный метод. Значит, для уменьшения предельной ошибки в
- 98. Математическая статистика Глава 2. Элементы теории корреляции. Известно, что процессы, протекающие в растениях и живых организмах,
- 99. Математическая статистика Глава 2. Элементы теории корреляции. Как найти параметры этих формул при условии, чтобы они
- 100. Математическая статистика Глава 2. Элементы теории корреляции. §1. Понятие о корреляции. В сельскохозяйственных науках, в отличие
- 101. Математическая статистика Глава 2. Элементы теории корреляции. §1. Понятие о корреляции. Например, связь урожайность - удобрения,
- 102. Математическая статистика Глава 2. Элементы теории корреляции. §1. Понятие о корреляции. Метод корреляции применяется для того,
- 103. Математическая статистика Глава 2. Элементы теории корреляции. §1. Понятие о корреляции. Первая задача корреляции: выявление на
- 104. Математическая статистика Глава 2. Элементы теории корреляции. §1. Понятие о корреляции. Вторая задача корреляции: определение степени
- 105. Математическая статистика Глава 2. Элементы теории корреляции. §1. Понятие о корреляции. Определение 1. Процесс нахождения связи
- 106. Математическая статистика Глава 2. Элементы теории корреляции. §1. Понятие о корреляции. При изучении влияния одних признаков
- 107. Математическая статистика Глава 2. Элементы теории корреляции. §2. Графическое изображение связи. Графическое изображение связи изучаемых явлений
- 108. Математическая статистика Глава 2. Элементы теории корреляции. §2. Графическое изображение связи. Ломаная, соединяющая эти точки, называется
- 109. Математическая статистика Глава 2. Элементы теории корреляции. §2. Графическое изображение связи. 2) Если экспериментальные данные располагаются
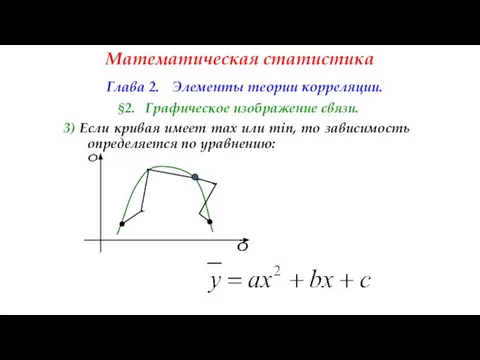
- 110. Математическая статистика Глава 2. Элементы теории корреляции. §2. Графическое изображение связи. 3) Если кривая имеет mах
- 111. Математическая статистика Глава 2. Элементы теории корреляции. §2. Графическое изображение связи. Для выявления функциональных зависимостей и
- 112. Математическая статистика Глава 2. Элементы теории корреляции. §2. Графическое изображение связи.
- 113. Математическая статистика Глава 2. Элементы теории корреляции. §3. Коэффициент корреляции. После того, как уравнение регрессии найдено,
- 114. Математическая статистика Глава 2. Элементы теории корреляции. §3. Коэффициент корреляции. - среднее значение факториального (причинного) признака
- 116. Математическая статистика Глава 2. Элементы теории корреляции. §3. Коэффициент корреляции. Величина коэффициента корреляции находится в пределах
- 117. Математическая статистика Глава 2. Элементы теории корреляции. §3. Коэффициент корреляции. 4) при |r|=0 связи между признаками
- 118. Математическая статистика Глава 2. Элементы теории корреляции. §3. Коэффициент корреляции. by/x - коэффициент регрессии, который опреде-
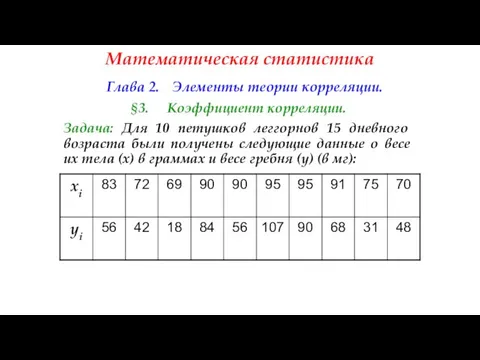
- 119. Математическая статистика Глава 2. Элементы теории корреляции. §3. Коэффициент корреляции. Задача: Для 10 петушков леггорнов 15
- 120. Математическая статистика Глава 2. Элементы теории корреляции. §3. Коэффициент корреляции. Требуется: 1) найти коэффициент корреляции и
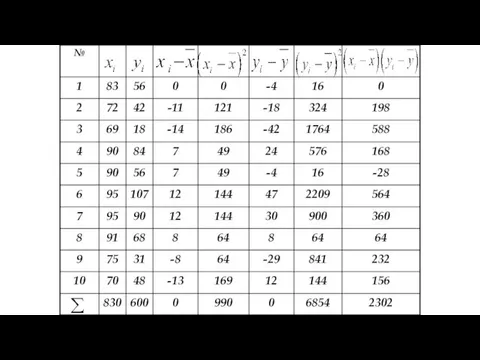
- 122. Математическая статистика Глава 2. Элементы теории корреляции. §3. Коэффициент корреляции. Вычисляем средние: 1) найдем коэффициент корреляции:
- 123. Математическая статистика Глава 2. Элементы теории корреляции. §3. Коэффициент корреляции. Вывод: между весом тела х и
- 124. Математическая статистика Глава 2. Элементы теории корреляции. §3. Коэффициент корреляции. Подставим в уравнение прямой регрессии:
- 126. Скачать презентацию

















































































































 Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений методом Гаусса Задание В12, открытого банка ЕГЭ по математике
Задание В12, открытого банка ЕГЭ по математике Высказывание. Операции над высказываниями
Высказывание. Операции над высказываниями Флексагон
Флексагон Элементы теории вероятностей. Цели и задачи
Элементы теории вероятностей. Цели и задачи Основные понятия и аксиомы стереометрии. Урок № 1
Основные понятия и аксиомы стереометрии. Урок № 1 Задачі з частинами і дробами
Задачі з частинами і дробами Магия чисел. Нумерология
Магия чисел. Нумерология Функция. Область определения функции
Функция. Область определения функции Mnohonásobná lineární regrese a korelace
Mnohonásobná lineární regrese a korelace Симплекс. Симплексное планирование
Симплекс. Симплексное планирование Тригонометрические функции острого угла
Тригонометрические функции острого угла Производная и дифференцируемость функции
Производная и дифференцируемость функции Архимед. (287 - 212 до н.э)
Архимед. (287 - 212 до н.э) Трёхзначные числа
Трёхзначные числа Антагонистические игры
Антагонистические игры Пропорції
Пропорції Функция. Область определения функции. Область значений функции
Функция. Область определения функции. Область значений функции Презентация на тему Мой любимый математик
Презентация на тему Мой любимый математик  Умножение. 5 класс
Умножение. 5 класс Конусы в нашей жизни
Конусы в нашей жизни  Сечение тел плоскостью
Сечение тел плоскостью Иоганн Карл Фридрих Гаусс
Иоганн Карл Фридрих Гаусс Сложение и вычитание 1-4
Сложение и вычитание 1-4 Логарифмы на ЕГЭ
Логарифмы на ЕГЭ Понятие цилиндра
Понятие цилиндра Шкала отношений
Шкала отношений Задачи с игральной костью
Задачи с игральной костью