то можно доказать, что погрешность приближенного решения стремится к нулю при
n→∞, то есть метод сходится и имеет при этом линейную скорость сходимости. (Сходится со скоростью геометрической прогрессии.)
Критерий сходимости
Если
дважды непрерывно дифференцируемая
функция и знак
сохраняется на рассматриваемом промежутке, то полученные приближения будут сходиться к корню монотонно. Если корень
уравнения
находится на отрезке [a,b], то производные
И
на этом промежутке непрерывны и сохраняют постоянные знаки и









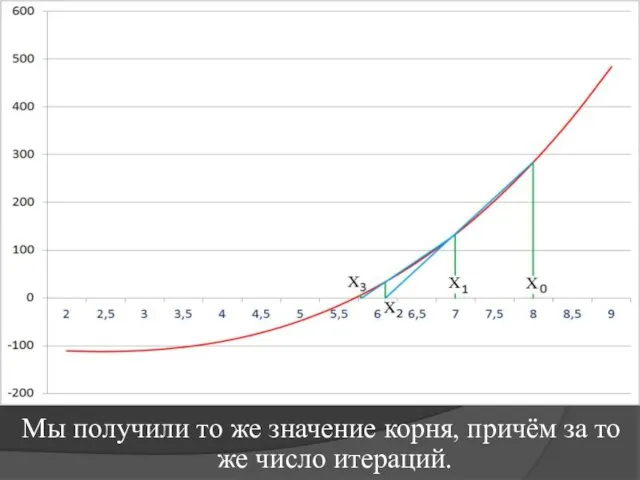

 Схема исследования функций и построение графиков
Схема исследования функций и построение графиков Прикладна статистика та ймовірнісні процеси
Прикладна статистика та ймовірнісні процеси Умножение дробей. Нахождение дроби от числа. Обобщающий урок -экскурсия
Умножение дробей. Нахождение дроби от числа. Обобщающий урок -экскурсия Математические диктанты для 8-х классов по геометрии
Математические диктанты для 8-х классов по геометрии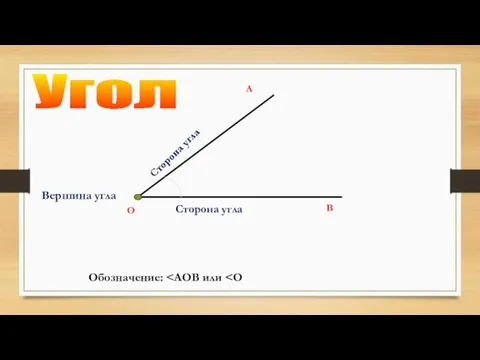 Виды углов. Измерение углов
Виды углов. Измерение углов Презентация по математике "Квадратичная функция, её свойства и график" - скачать
Презентация по математике "Квадратичная функция, её свойства и график" - скачать  Правила действий с обыкновенными дробями
Правила действий с обыкновенными дробями Конструктор (4)
Конструктор (4) Площадь трапеции
Площадь трапеции Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Определение формы парной корреляционной зависимости
Определение формы парной корреляционной зависимости Математика
Математика Методы решения системы трёх линейных уравнений с тремя неизвестными
Методы решения системы трёх линейных уравнений с тремя неизвестными Урок математики 1 класс. Числовой луч
Урок математики 1 класс. Числовой луч Задачи на проценты. Подготовка к ЕГЭ. Задания В1
Задачи на проценты. Подготовка к ЕГЭ. Задания В1 Описанная окружность
Описанная окружность Признаки подобия треугольников
Признаки подобия треугольников Площадь прямоугольника Ладанова И.В. – учитель математики МКОУ «Верх-Жилинская ООШ» Косихинский район Алтайский край
Площадь прямоугольника Ладанова И.В. – учитель математики МКОУ «Верх-Жилинская ООШ» Косихинский район Алтайский край  Золотое сечение
Золотое сечение Окружность. Примеры решения задач. Подготовка к ОГЭ
Окружность. Примеры решения задач. Подготовка к ОГЭ Решение квадратных уравнений. Алгебра 8 класс
Решение квадратных уравнений. Алгебра 8 класс Закон больших чисел и центральная предельная теорема
Закон больших чисел и центральная предельная теорема Вычитание из чисел 8 9 10. Связь сложения и вычитания
Вычитание из чисел 8 9 10. Связь сложения и вычитания Сложение и вычитание в пределах 5
Сложение и вычитание в пределах 5 Статистические наблюдения
Статистические наблюдения Интегральное исчисление функций одной переменной
Интегральное исчисление функций одной переменной Основи роботи з MathCAD
Основи роботи з MathCAD Кратные единицы
Кратные единицы