Содержание
- 2. Вспомогательная задача к ЗЛП (1): (2) Вектор составлен из естественных переменных ЗЛП (1.) и искусственных переменных,
- 3. Искусственные переменные не несут никакого экономического смысла. Они необходимы только для поиска начального БДП. Единичные векторы
- 4. Теорема. (О существовании плана ЗЛП). Пусть оптимальный план ЗЛП (2), тогда: Если , то план является
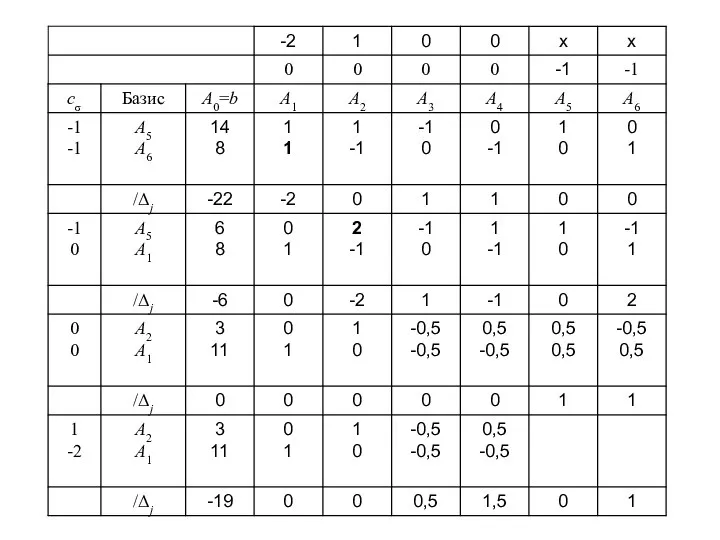
- 5. П р и м е р: Рассмотрим ЗЛП: Приведем данную ЗЛП к каноническому виду:
- 6. Единичного базиса нет, поэтому построим вспомогательную задачу, предварительно введя две искусственные переменные х5 ≥ 0 и
- 8. Решив данную вспомогательную задачу симплекс-методом, мы найдем ее оптимальный план и значение целевой функции на этом
- 9. Признак неограниченности целевой функции ЗЛП в канонической форме: Пусть х0 = (х10, х20,…, хn0) - БДП
- 10. В уравнении (2) хσ0 представляет часть исходного вектора х0 , из которого удалены нулевые (свободные) компоненты.
- 11. Теорема. О неразрешимости ЗЛП. Если для некоторого БДП х0 существует Δk
- 12. Пример: Единичный базис состоит из векторов А3, А4, А5. Вырожденный БДП х0 = (0; 0; 1;
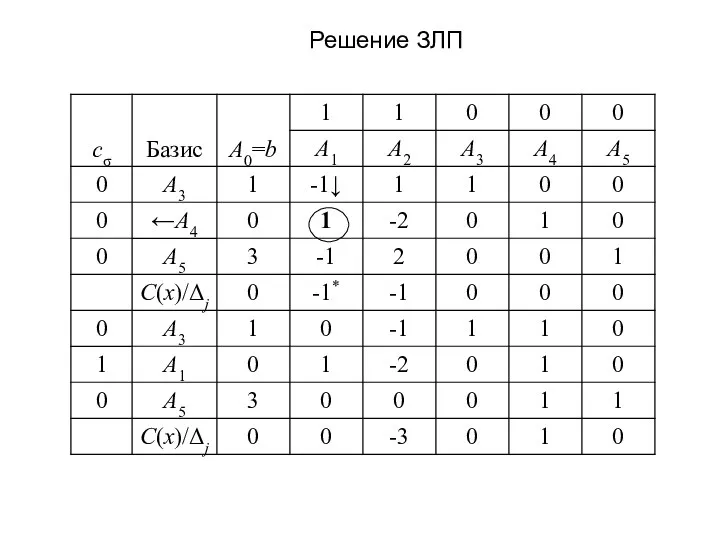
- 13. Решение ЗЛП
- 15. Скачать презентацию










 Пропорции
Пропорции Презентация на тему Множество. Элемент множества.
Презентация на тему Множество. Элемент множества. Независимая переменная имеет больше двух уровней
Независимая переменная имеет больше двух уровней Выборочное наблюдение
Выборочное наблюдение Теория вероятностей. Обобщающий урок: «Решение простейших вероятностных задач»
Теория вероятностей. Обобщающий урок: «Решение простейших вероятностных задач» Найдите все значения параметра a,
Найдите все значения параметра a, ЕГЭ Профиль - Задание 3
ЕГЭ Профиль - Задание 3 Задания на логику
Задания на логику Делимость чисел. Простые и составные числа. Признаки делимости
Делимость чисел. Простые и составные числа. Признаки делимости Действия с рациональными числами (интерактивный тест) Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей»
Действия с рациональными числами (интерактивный тест) Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей» Формулы сокращенного умножения. 7 класс
Формулы сокращенного умножения. 7 класс Математические открытия
Математические открытия Действия с десятичными дробями
Действия с десятичными дробями Презентация по математике "Итоговый тест по математике" - скачать
Презентация по математике "Итоговый тест по математике" - скачать  Пирамида
Пирамида Решение задач, с помощью квадратных уравнений. Учитель математики ГБОУ центр образования №170 Колпинского района Санкт-Петербур
Решение задач, с помощью квадратных уравнений. Учитель математики ГБОУ центр образования №170 Колпинского района Санкт-Петербур Первый признак равенства треугольников
Первый признак равенства треугольников Урок математики в 5 классе Учитель математики высшей категории МБОУ «Бриентской СОШ» Бакеева И. Р.
Урок математики в 5 классе Учитель математики высшей категории МБОУ «Бриентской СОШ» Бакеева И. Р.  Десятичные дроби и действия над ними
Десятичные дроби и действия над ними  «О дюймах, вершках и сантиметрах». Одни лапти без меры плетутся, да на всякую ногу приходятс
«О дюймах, вершках и сантиметрах». Одни лапти без меры плетутся, да на всякую ногу приходятс Штангенциркуль
Штангенциркуль Умножение и деление степеней. Закономерности
Умножение и деление степеней. Закономерности История теоремы Пифагора
История теоремы Пифагора Статистические характеристики: среднее арифметическое, мода, медиана
Статистические характеристики: среднее арифметическое, мода, медиана Презентация на тему Сложение чисел с разными знаками 6 класс
Презентация на тему Сложение чисел с разными знаками 6 класс  Тригонометрические неравенства
Тригонометрические неравенства Конус. Площадь поверхности конуса. Усеченный конус
Конус. Площадь поверхности конуса. Усеченный конус Работа с текстовыми задачами. Тест
Работа с текстовыми задачами. Тест