Содержание
- 2. Будем считать, что в приведенной форме (2) базисные вектора расположены первыми по порядку, т.е. В качестве
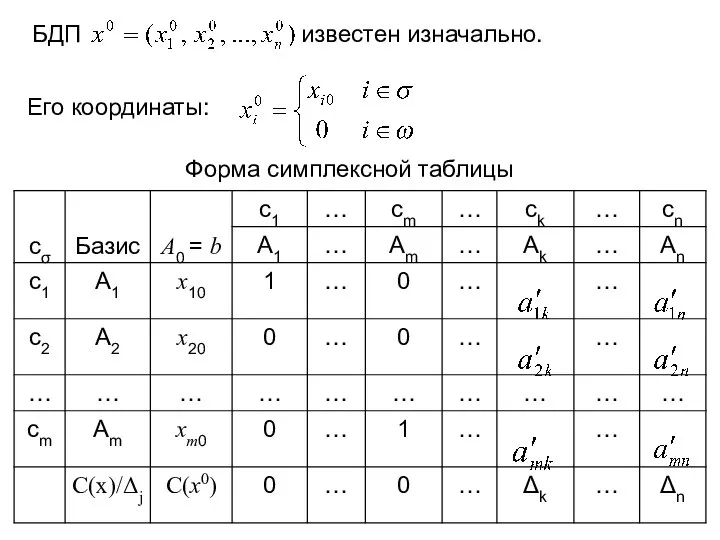
- 3. БДП известен изначально. Его координаты: Форма симплексной таблицы
- 4. cσ – коэффициенты целевой функции при базисных переменных; А1, А2, …, Аn – векторы-столбцы решаемой задачи;
- 5. Значение целевой функции на этом плане вычисляется по формуле: Двойственные оценки Δj вычисляются по формуле: Переход
- 6. Правило 2. Определение номера вектора, выводимого из базиса. Необходимо определить номер r выводимого из базиса вектора
- 7. Опр. Элемент вводимого в базис, и вектора, выводимого из базиса, называется ведущим (или разрешающим) элементом симплексной
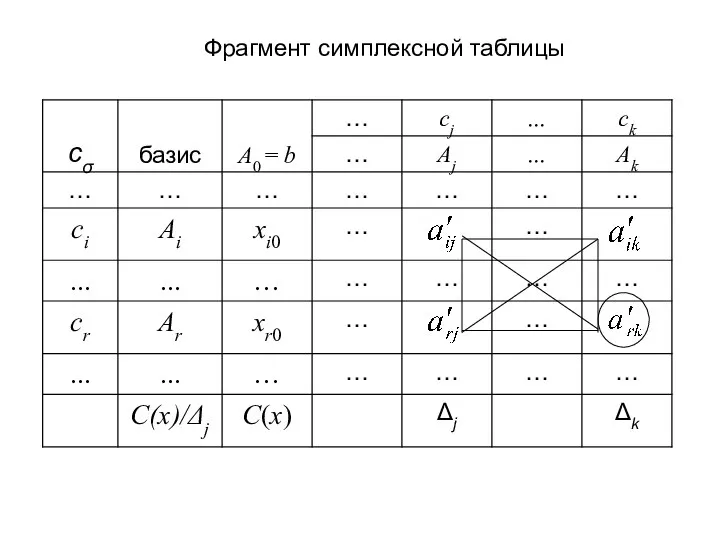
- 8. Фрагмент симплексной таблицы
- 9. δik - символ Кронекера (6) Формулы пересчета элементов симплекс-таблицы при переходе к новому базису:
- 10. Координаты нового плана вычисляются по формулам: (7) Новые двойственные оценки: (8)
- 11. Значение целевой функции на новом плане равно (9) Теорема. Для нового базисного допустимого плана имеет место
- 12. П р и м е р . Приведем ЗЛП к каноническому виду путем введения дополнительных переменных:
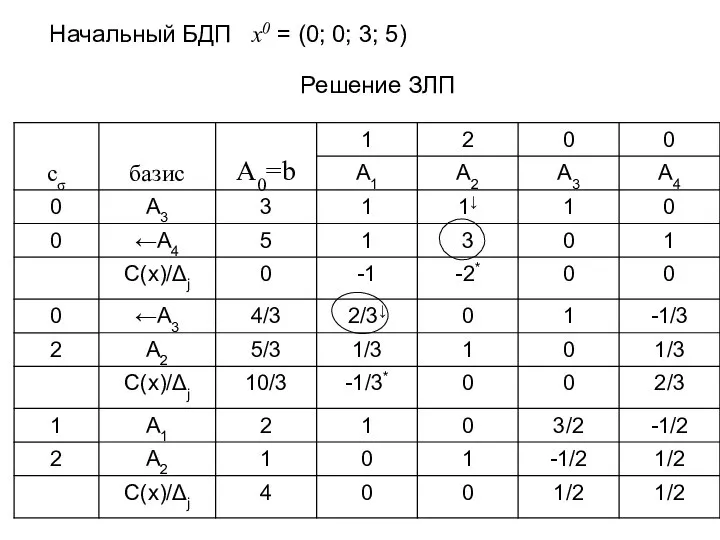
- 13. Начальный БДП х0 = (0; 0; 3; 5) Решение ЗЛП
- 15. Скачать презентацию









 Треугольники, 7 класс
Треугольники, 7 класс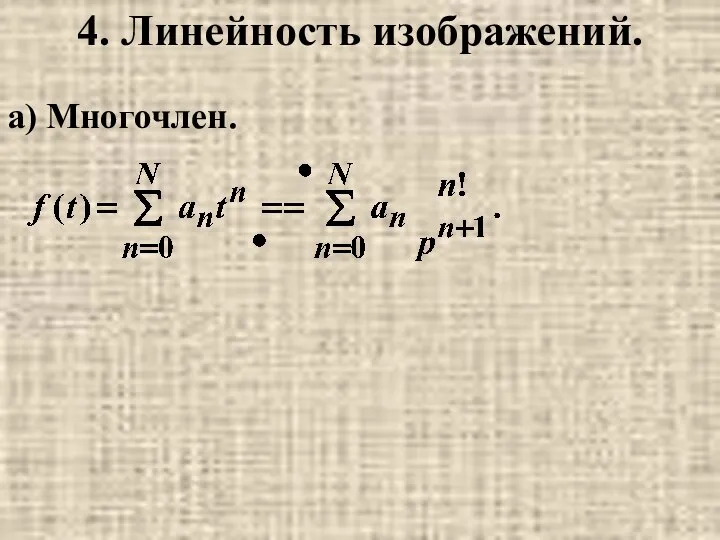 Линейность изображений
Линейность изображений Chapter 3. Polynomial and Rational Functions. 3.2 Polynomial Functions and Their Graphs
Chapter 3. Polynomial and Rational Functions. 3.2 Polynomial Functions and Their Graphs Признаки делимости на 10, на 5, на 2
Признаки делимости на 10, на 5, на 2 Арифметические действия с десятичными дробями Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей»
Арифметические действия с десятичными дробями Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей»  Текстовые задачи на движение
Текстовые задачи на движение Тела вращения. Цилиндр. Сечение. Вписанная и описанная призма. Конус. Сечение. Вписанная и описанная пирамида. Шар. Симметрия
Тела вращения. Цилиндр. Сечение. Вписанная и описанная призма. Конус. Сечение. Вписанная и описанная пирамида. Шар. Симметрия Нахождение процентов от числа и числа по его проценту. 5 класс
Нахождение процентов от числа и числа по его проценту. 5 класс Точка, линия, прямая и кривая линии. Число 2. Цифра 2
Точка, линия, прямая и кривая линии. Число 2. Цифра 2 Следствия из аксиом I - III
Следствия из аксиом I - III Признаки сходимости несобственных интегралов. Теорема 1. Признак сравнения несобственных интегралов 1 рода
Признаки сходимости несобственных интегралов. Теорема 1. Признак сравнения несобственных интегралов 1 рода Условная вероятность
Условная вероятность Подготовка к введению задач в 2 действия
Подготовка к введению задач в 2 действия Делимость натуральных чисел
Делимость натуральных чисел Лента Мебиуса. Все гениальное просто. (приложение)
Лента Мебиуса. Все гениальное просто. (приложение)  Подготовка к ГИА. Нахождение знаков коэффициентов квадратичной функции по графику
Подготовка к ГИА. Нахождение знаков коэффициентов квадратичной функции по графику 20161216_den_fibonachchi
20161216_den_fibonachchi Симметрические многочлены
Симметрические многочлены Три признака параллельности двух прямых
Три признака параллельности двух прямых Решение практико-ориентированных задач ЕГЭ
Решение практико-ориентированных задач ЕГЭ Пересекающиеся прямые. Вертикальные и смежные углы
Пересекающиеся прямые. Вертикальные и смежные углы Полуправильные многоугольники. Длина и площадь
Полуправильные многоугольники. Длина и площадь Криволинейные интегралы 2 рода
Криволинейные интегралы 2 рода Натуральные числа. Обобщающий урок
Натуральные числа. Обобщающий урок Логико-когнетивные основы урока алгебры
Логико-когнетивные основы урока алгебры Определение угла. Развернутый угол
Определение угла. Развернутый угол Інтегральне числення
Інтегральне числення Решение заданий ЕГЭ. Урок-консультация. 11 класс
Решение заданий ЕГЭ. Урок-консультация. 11 класс