Метод мажорант

«majorer» -
объявлять большим

«minorer» -
объявлять меньшим.

Название метода мажорант происходит
от

Мажорантой
данной функции f(х)
на множестве Р, называется
такое число М,

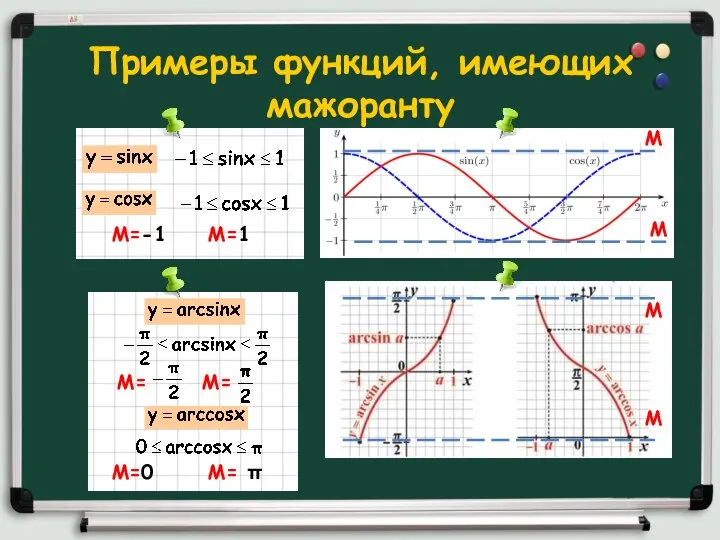
Примеры функций, имеющих мажоранту

М

М

М

М

М=-1

М=1

М=

М=

М=0

М= π

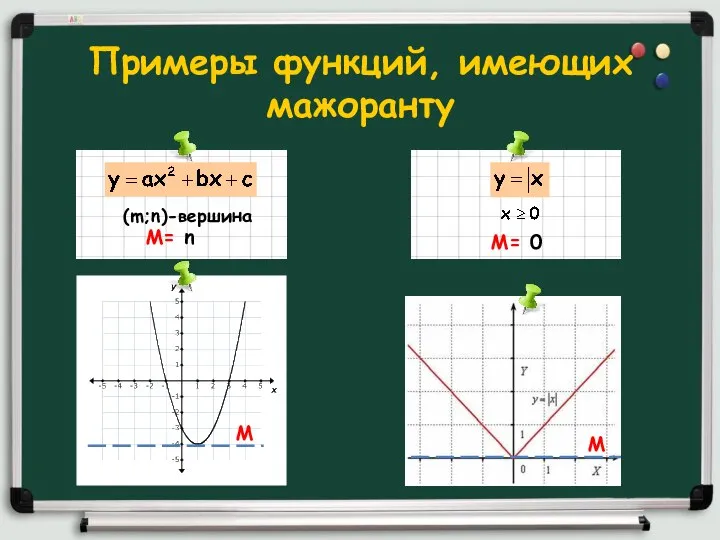
Примеры функций, имеющих мажоранту

М

М

(m;n)-вершина

М= n

М= 0

Оценить левую часть: f(x)

Оценить правую часть: g(x)

Если f(x)≥М , при

Решить уравнение:

Решение:

Оценим правую часть уравнения:

Оценим левую часть уравнения:

C одной стороны

с другой

Решение системы, а значит и уравнения: х=1.

Ответ:
х=1

Решим первое уравнение системы:

Решить уравнение:

Решение:

ОДЗ:

Оценим левую часть уравнения:

Перемножим два неравенства:

и

Оценим правую часть уравнения:

Складываем двойные неравенства:

Получим:

C одной стороны

с другой стороны

Уравнение

имеет решение,

Решим второе уравнение системы:

Уравнение имеет решение, если:

Если:

то:

у

х

Ответ:
х=2πn,
n Ɛ Z

Решить неравенство

Решение:

ОДЗ: х ˃ 0

Преобразуем выражение:

Если х ˃0, то

,тогда

для

C одной стороны

-наибольшее значение функции

,с другой стороны

Неравенство

имеет решение, если

Решение системы,

Решить неравенство

Решение:

ОДЗ:

Преобразуем неравенство, умножив левую и правую части на

,то

Оценим левую

Решим второе уравнение системы

C одной стороны

с другой стороны

Неравенство

имеет решение, если

Найти все значения параметра а, при каждом из которых система имеет

у

х

2

-2

2

-2

Оценим левую часть уравнения:

Оценим правую часть уравнения:

C одной стороны

с другой стороны

Уравнение

имеет

Примеры уравнений и неравенств, решаемых методом мажорант