Содержание
- 2. СОДЕРЖАНИЕ Метод Флетчера-Ривза Алгоритм Дэвидона - Флетчера - Пауэлла Метод кубической интерполяции
- 3. МЕТОД ФЛЕТЧЕРА-РИВЗА
- 4. МЕТОД СОПРЯЖЕННЫХ ГРАДИЕНТОВ Формирует направления поиска, в большей мере соответствующие геометрии минимизируемой функции. Определение. Два n-мерных
- 5. СТРАТЕГИЯ МЕТОДА ФЛЕТЧЕРА-РИВСА Состоит в построении последовательности точек {xk}, k=0, 1, 2, ... таких, что f(xk+1)
- 6. СХОДИМОСТЬ МЕТОДА Теорема 1. Если квадратичная функция f(x) = (х, Нх) + (b, х) + а
- 7. Теорема 2 гарантирует сходимость последовательности {xk} к стационарной точке x*, где ▽f(x*)=0. Поэтому найденная точка x*
- 8. АЛГОРИТМ ДЭВИДОНА - ФЛЕТЧЕРА - ПАУЭЛЛА Рассмотрим алгоритм Дэвидона - Флетчера - Пауэлла минимизации дифференцируемой функции
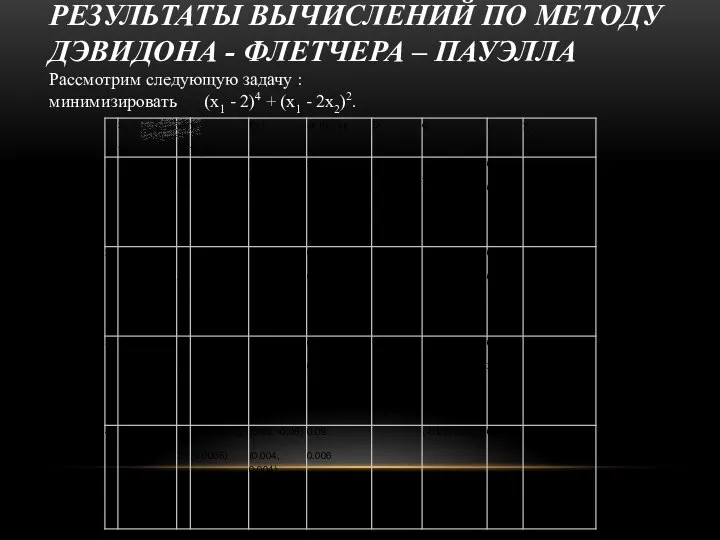
- 9. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ ПО МЕТОДУ ДЭВИДОНА - ФЛЕТЧЕРА – ПАУЭЛЛА Рассмотрим следующую задачу : минимизировать (x1 -
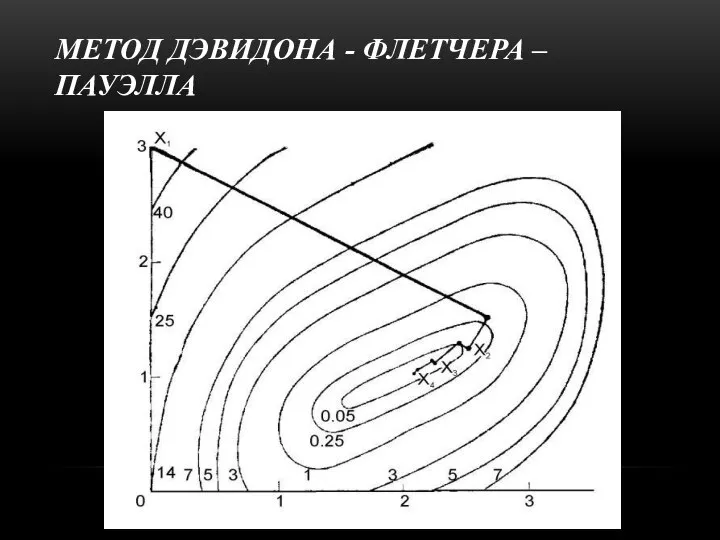
- 10. МЕТОД ДЭВИДОНА - ФЛЕТЧЕРА – ПАУЭЛЛА
- 11. МЕТОД КУБИЧЕСКОЙ ИНТЕРПОЛЯЦИИ При решении реальных задач редко приходится иметь дело с функциями одной переменной. Однако
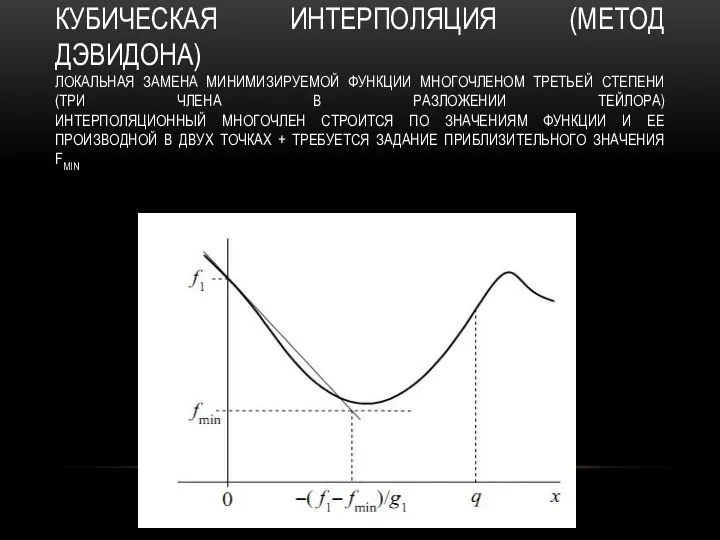
- 12. КУБИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ (МЕТОД ДЭВИДОНА) ЛОКАЛЬНАЯ ЗАМЕНА МИНИМИЗИРУЕМОЙ ФУНКЦИИ МНОГОЧЛЕНОМ ТРЕТЬЕЙ СТЕПЕНИ (ТРИ ЧЛЕНА В РАЗЛОЖЕНИИ ТЕЙЛОРА)
- 13. ЗАКЛЮЧЕНИЕ Метод сопряженных градиентов формирует направления поиска, в большей мере соответствующие геометрии минимизируемой функции. Первоначально метод
- 15. Скачать презентацию









 Счастливый случай. 7 класс
Счастливый случай. 7 класс Педагогические, теоретические и практические аспекты проблемы ЕГЭ. Решение задания 13 ЕГЭ - 2016
Педагогические, теоретические и практические аспекты проблемы ЕГЭ. Решение задания 13 ЕГЭ - 2016 Подготовка к ЕГЭ
Подготовка к ЕГЭ Решение задач. Касательная к окружности
Решение задач. Касательная к окружности Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Уравнение окружности и прямой
Уравнение окружности и прямой Решение задач С1 3-мя способами
Решение задач С1 3-мя способами Урок в 5 классе тема «Умножение десятичных дробей»
Урок в 5 классе тема «Умножение десятичных дробей»  Площадь криволинейной трапеции
Площадь криволинейной трапеции Урок математики 4 «А» класс Учитель Гондак О.В.
Урок математики 4 «А» класс Учитель Гондак О.В.  Математические модели
Математические модели Дробные выражения. Устный счет
Дробные выражения. Устный счет Презентация по математике "Фалес" - скачать
Презентация по математике "Фалес" - скачать  Линейные фракталы
Линейные фракталы Линейная независимость
Линейная независимость Выражения. Решение задач
Выражения. Решение задач Полуправильные многогранники
Полуправильные многогранники Область истинности выражения
Область истинности выражения МОУ СОШ № 256 г.Фокино Каратанова Марина Николаевна __
МОУ СОШ № 256 г.Фокино Каратанова Марина Николаевна __ Подобие треугольников
Подобие треугольников График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Скалярное произведение векторов
Скалярное произведение векторов Производная и дифференциал. Техника дифференцирования элементарных функций
Производная и дифференциал. Техника дифференцирования элементарных функций Решение задач разными способами
Решение задач разными способами Гипербола. Кривая второго порядка
Гипербола. Кривая второго порядка Решение задач с использованием признаков равенства треугольников
Решение задач с использованием признаков равенства треугольников Сумма n-первых членов арифметической прогрессии
Сумма n-первых членов арифметической прогрессии Теория систем. Система. Классификация систем. (Тема 3)
Теория систем. Система. Классификация систем. (Тема 3)