Множества. Логические символы. (Лекция 1)

Кудрявцев Л.Д. Курс математического анализа, т.1-2
Ильин В.А., Поздняк Э.Г. Основы математического

Учебные пособия

Изучение математики
- совершенствует общую культуру мышления, дисциплинирует ее, приучает человека логически

1. МНОЖЕСТВА

- знак принадлежности
- квантор всеобщности
- квантор существования
- знак логического следования
-

Множества. Способы задания.

def

A={a,b,c,d};

A ={x P( x)};

{a} - одноэлементное множество;
- пустое множество
Действительные

Отношения между множествами.
Определение 1.1. Множества A и B называются равными, если

Свойства равенства:

A=A
A=B, B=C  A=C
A=B  B=A

(рефлексивность); (транзитивность); (симметричность).

Неравенство множеств обозначают

■

A

Определение 1.2.

Множество A (A  ) называется подмножеством множества B (B

Операции над множествами.

V – основное или универсальное множество.
1) В планиметрии V =R2
2)

Один из величайших

математиков

петербургской академии Леонард Эйлер

(1707–1783) за свою долгую

жизнь

написал более 850 научных работ. В одной из

Джон Венн ( John Venn; 4 августа 1834, Халл (Йоркшир) —

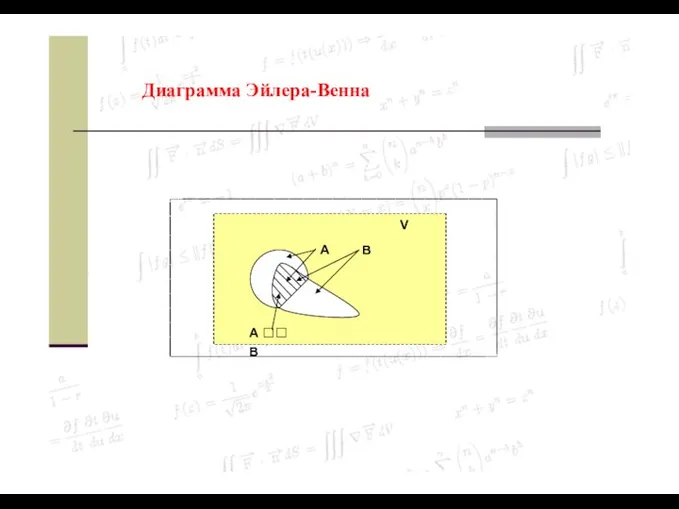
Диаграмма Эйлера-Венна

A  B

V

A

B

Свойства объединения множеств.

■ 1) A  B = B  A
■ 2) A

Определение 1.4.

Пересечением множеств A и B называется множество A  B,

Диаграмма Эйлера-Венна

V

A

B

A  B

Свойства пересечения множеств.

(коммутативность), (ассоциативность).

■ 1) A  B = B  A
■ 2)

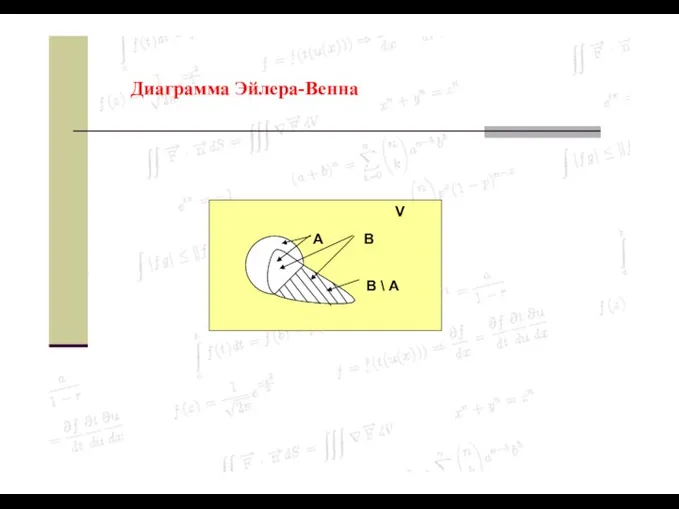
Определение 1.5.

Разностью двух множеств B и A называется множество B \

Диаграмма Эйлера-Венна

V

A

B

B \ A

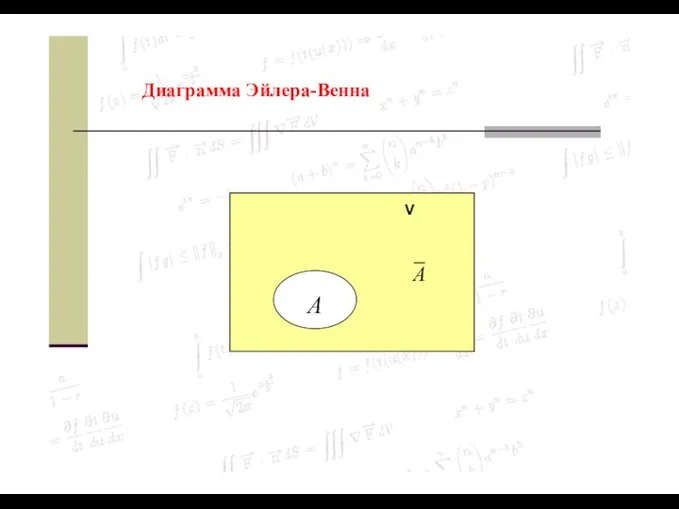
Определение 1.6.

Разность V \ A называется дополнением множества A до

универсального множества

Диаграмма Эйлера-Венна

V
A
A

Определение 1.7.
Пара элементов ( x ; y ), x  A,

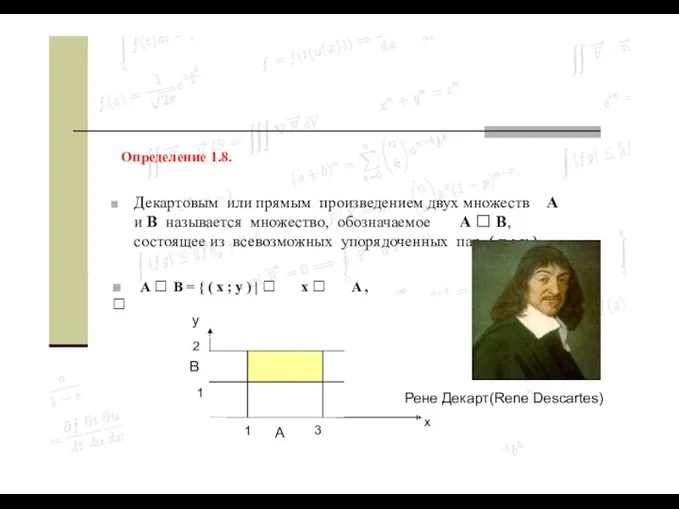
Определение 1.8.

Декартовым или прямым произведением двух множеств A и B называется множество, обозначаемое A

Несколько приятелей встретились на вокзале, чтобы поехать за город в лес.

Множество Мандельброта

Отображение множеств. Эквивалентность множеств.

Пусть A и B - произвольные множества.
Пусть f

Определение отображения:
■ f : A  B   a  A

Определение 1.9
Отображение называется инъекцией, если для любых элементов x1, x2 ∈

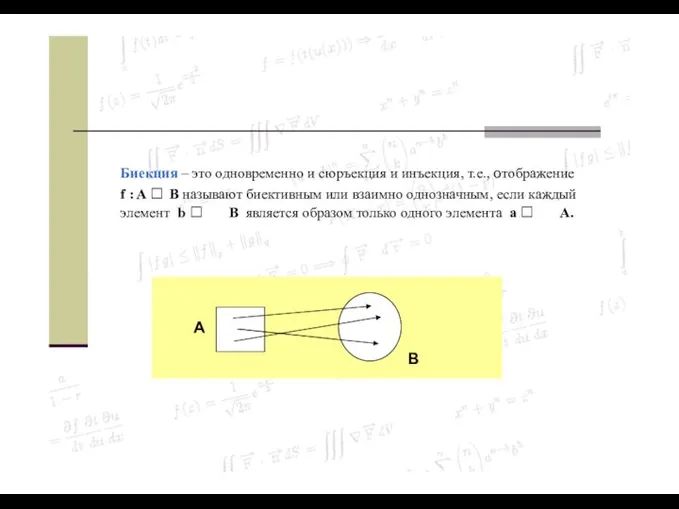
Биекция – это одновременно и сюръекция и инъекция, т.е., отображение
f :

f – взаимно однозначное отображение   b  B 

Определение 1.10.
Отображение f -1 : B→A называется обратным к отображению
f :

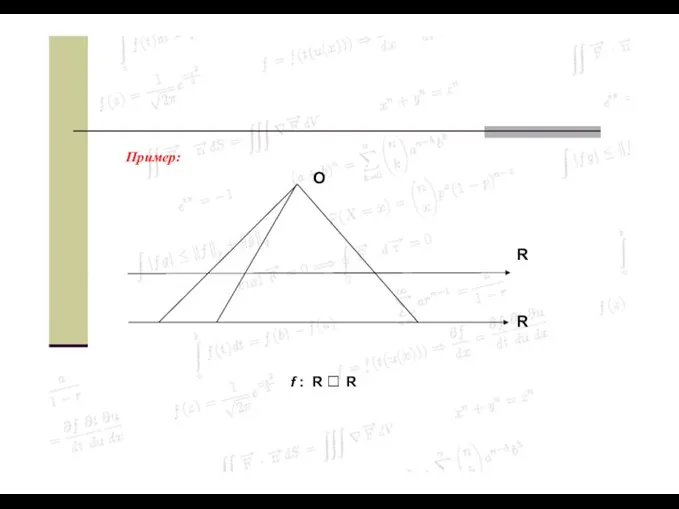
Пример:
О

R

R
f : R  R

Определение 1.11

Два множества A и B называются эквивалентными (равномощными), если существует хотя бы одно взаимно однозначное

Числовые множества

Множества, элементами которых являются числа, называются числовыми.
Примерами числовых множеств являются:
N

выполняются: коммутативность, ассоциативность, дистрибутивность;

Множество натуральных чисел N.
■ N = {1, 2, 3, …}.
Свойства:
■ 1)
■
■
■
■
■

2)

Множество целых чисел Z
Z = { …, -2, -1, 0, 1,

Множество рациональных чисел Q.
Q = { q = p / n

Множество действительных чисел R.

■
■
■

Свойства:
R – упорядоченно;
R –бесконечно;

Множество R плотное: между любыми двумя

Множество R непрерывное.
Пусть множество R разбито на два непустых класса А

Последовательности
Определение 1.12
Пусть каждому натуральному числу n=1, 2, ... приведено в соответствие

Примеры последовательностей:

В случае 7) не видно, как написать общую формулу для

Определение 1.13
Последовательность {хп} называется ограниченной, если существует такое число М >

Предел последовательности
Метод пределов есть основной метод, на котором базируется математический анализ
Можно

Определение 1.14
Число а называется пределом последовательности {xn} если для любого положительного

Геометрический смысл определения предела последовательности.
Неравенство
равносильно неравенствам -  < хn -