Содержание
- 2. Теория игр 1. Основные понятия теории игр. Теория игр - Конфликтная ситуация Черты конфликтной ситуации: Игра
- 3. Теория игр по количеству игроков: - парная - множественная Классификация игр по количеству стратегий: конечная бесконечная
- 4. Теория игр 2. Постановка парной антагонистической игры. Дано: A1,A2,…,Am - стратегии игрока А (чистые стратегии игрока
- 5. Теория игр Платежная матрица:
- 6. Теория игр Цель теории игр – Решить игру – Оптимальными Цель игрока А – получить максимальный
- 7. Теория игр Пример. Найти верхнюю и нижнюю цену игры, платежная таблица игры имеет вид:
- 8. Теория игр 4. Принцип доминирования. Цель - уменьшить размерность задачи (редуцировать платежную матрицу). Принцип доминирования –
- 9. Теория игр 5. Решение игры в чистых стратегиях. Если α = β, то игра имеет седловую
- 10. Моделирование конфликтных ситуаций в экономике Матричные игры и задачи линейного программирования. Между матричными играми и линейным
- 11. Моделирование конфликтных ситуаций в экономике Вводя переменные x1=p1/v, x2=p2/v,… и, учитывая, что игрок А стремится получить
- 13. Скачать презентацию









 Дифференциальные уравнения. (Лекция 3)
Дифференциальные уравнения. (Лекция 3) Поиск оптимального пути в 3D
Поиск оптимального пути в 3D Расстояние от точки до плоскости. Теорема о трех перпендикулярах
Расстояние от точки до плоскости. Теорема о трех перпендикулярах Проект по математике. Фигуры на координатной плоскости
Проект по математике. Фигуры на координатной плоскости Математический диктант. 4 класс
Математический диктант. 4 класс Обыкновенные дроби. Задания для устного счета. 8 класс
Обыкновенные дроби. Задания для устного счета. 8 класс Теорема Пифагора
Теорема Пифагора Математическое путешествие по сказке (для дошкольников)
Математическое путешествие по сказке (для дошкольников) Презентация по математике "Урок одного уравнения" - скачать бесплатно
Презентация по математике "Урок одного уравнения" - скачать бесплатно Сложение чисел с разными знаками
Сложение чисел с разными знаками Формы выражения статистических показателей
Формы выражения статистических показателей Ум заключается не только в знании, но и в умении прилагать знание в дело Аристотель
Ум заключается не только в знании, но и в умении прилагать знание в дело Аристотель  Обратные действия
Обратные действия Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Иллюзии в математике
Иллюзии в математике Предикаты и кванторы. Действия над предикатами и их свойства
Предикаты и кванторы. Действия над предикатами и их свойства Решение логарифмических уравнений и неравенств
Решение логарифмических уравнений и неравенств Introductory statistics
Introductory statistics Угол поворота. Радианная мера угла
Угол поворота. Радианная мера угла Тригонометрические уравнения
Тригонометрические уравнения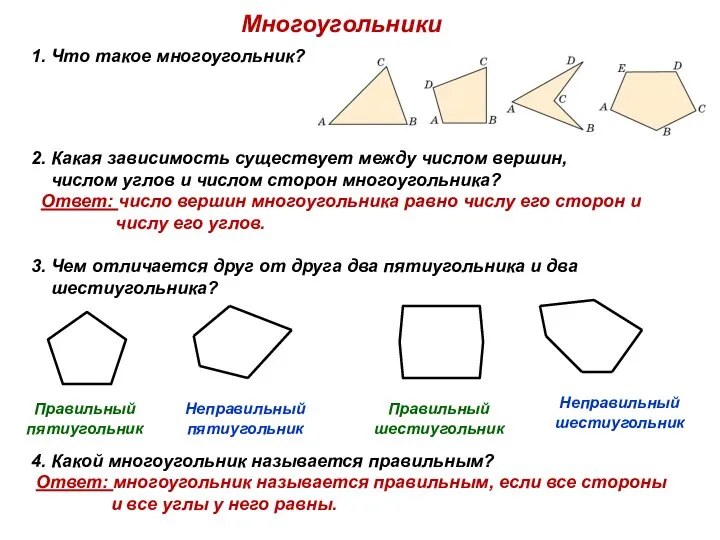 Многоугольники
Многоугольники Моделирование систем
Моделирование систем Четырехугольники. Определение
Четырехугольники. Определение Многозначные числа
Многозначные числа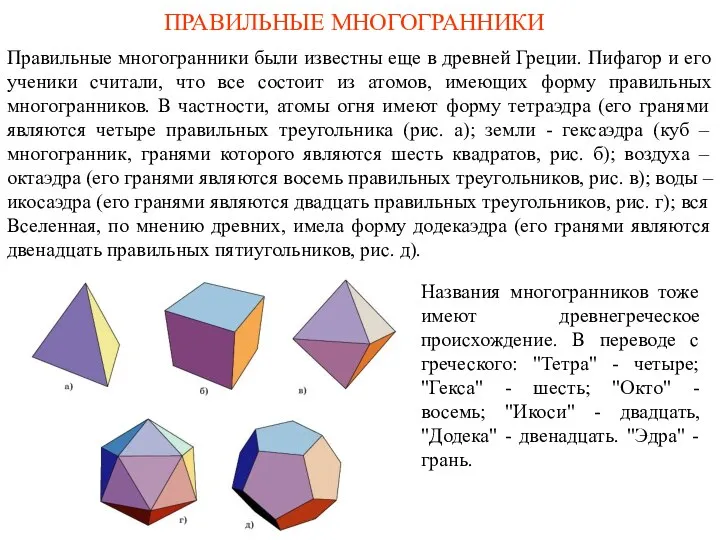 Правильные многогранники
Правильные многогранники Счет 1, 2, 3, 4
Счет 1, 2, 3, 4 Методы многопарметрической оптимизации
Методы многопарметрической оптимизации Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний
Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний