Содержание
- 2. «Возрастание и убывание функций. Экстремумы функций» Занятие №33 в ГБОУ СПО «Серпуховский машиностроительный техникум М.О.» Мурашова
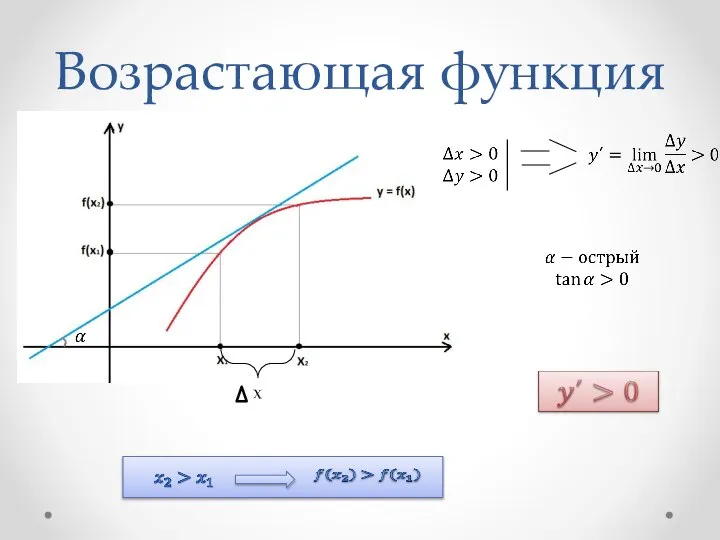
- 3. Возрастающая функция х
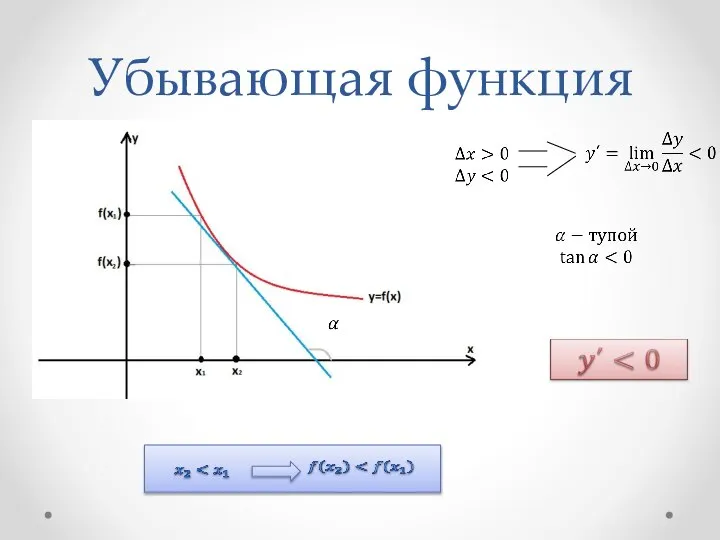
- 4. Убывающая функция
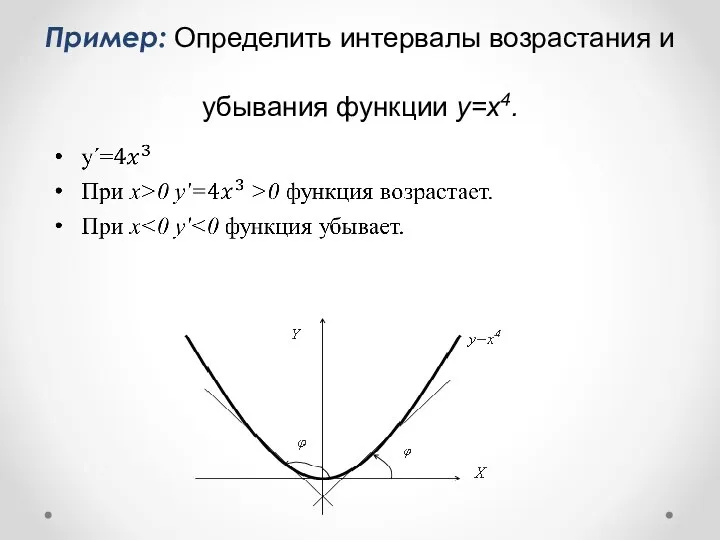
- 5. Пример: Определить интервалы возрастания и убывания функции y=x4.
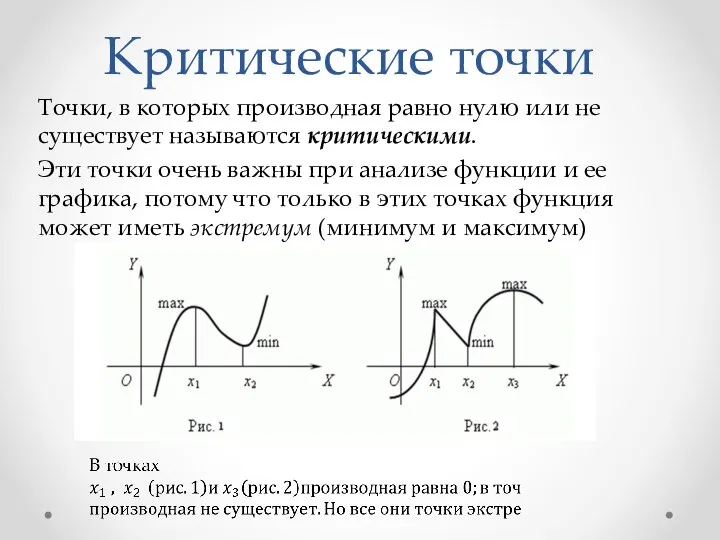
- 7. Критические точки Точки, в которых производная равно нулю или не существует называются критическими. Эти точки очень
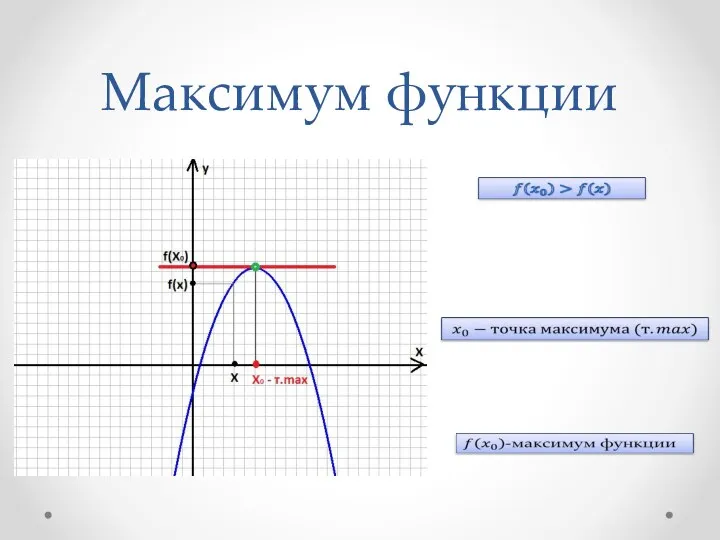
- 8. Максимум функции
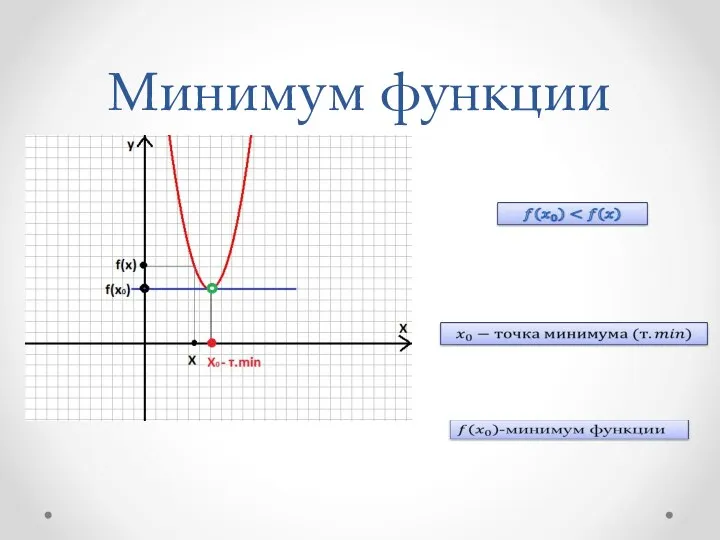
- 9. Минимум функции
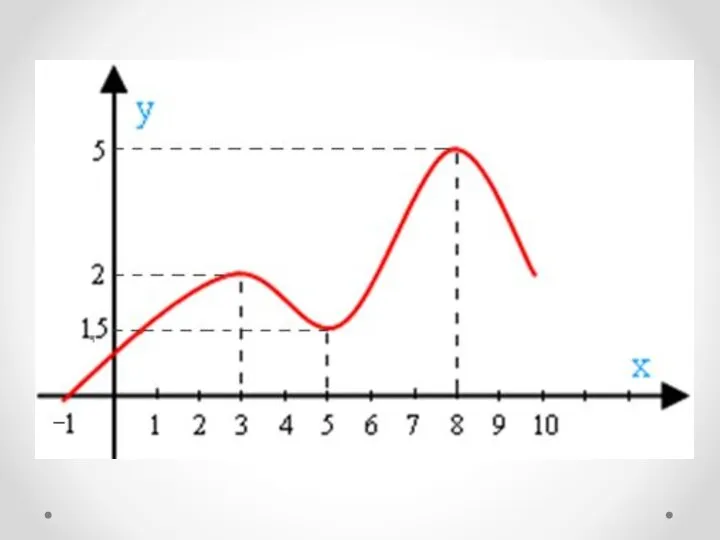
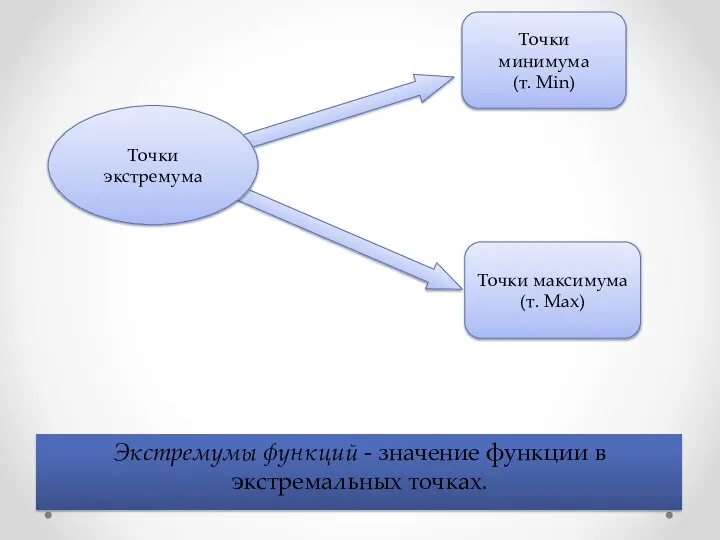
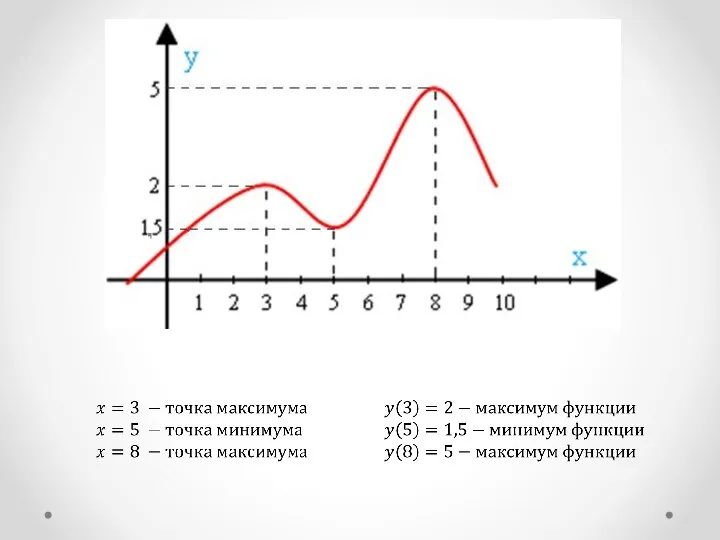
- 10. Экстремумы функций - значение функции в экстремальных точках. Точки минимума (т. Min) Точки экстремума Точки максимума
- 12. Необходимое условие экстремума (Теорема Ферма) Если точка х0 является точкой экстремума функции f и в этой
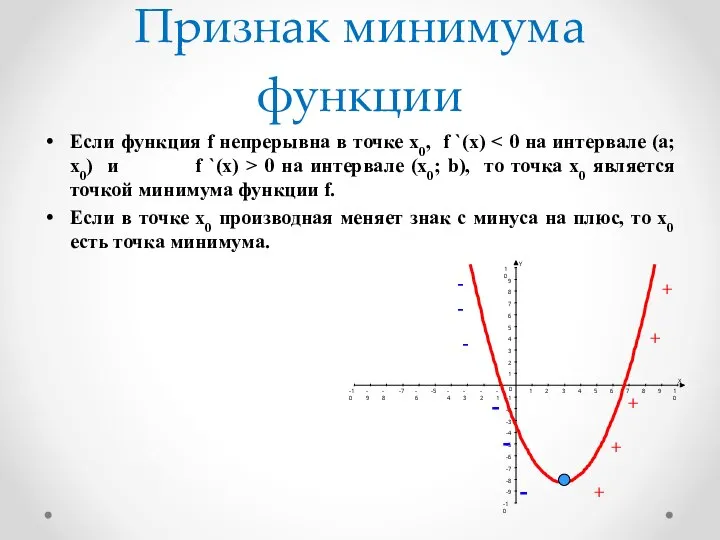
- 14. Признак минимума функции Если функция f непрерывна в точке х0, f `(x) 0 на интервале (х0;
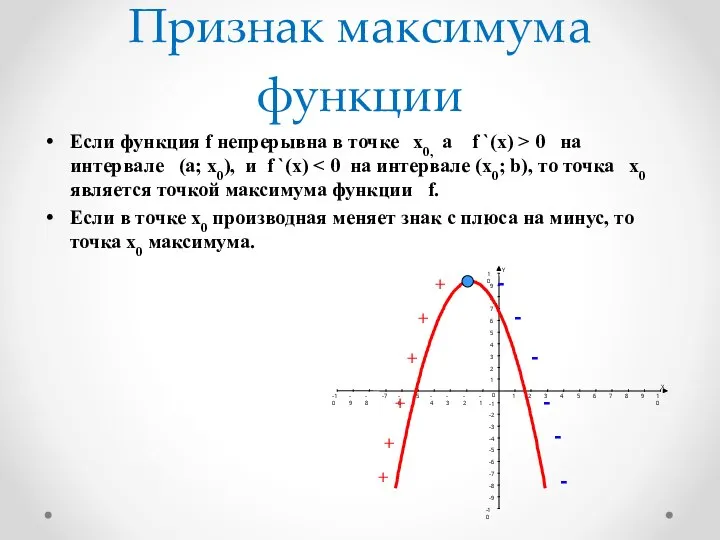
- 15. Признак максимума функции Если функция f непрерывна в точке х0, а f `(x) > 0 на
- 16. Алгоритм нахождения интервалов монотонности и нахождения экстремумов функции 1) Найти область определения функции 2) Вычислить производную
- 17. Пример
- 18. Исследовать функции на монотонность, найти экстремумы
- 19. Домашнее задание -выучить определения, теоремы, записанные в теоретической части занятия; -разобрать примеры, предложенные в процессе изучения
- 21. Скачать презентацию







 Единицы измерения длины. Сантиметр
Единицы измерения длины. Сантиметр Аттестационная работа. Программа внеурочной деятельности по математике В мире чисел и задач. (7 класс)
Аттестационная работа. Программа внеурочной деятельности по математике В мире чисел и задач. (7 класс) Площадь прямоугольника
Площадь прямоугольника Метрологическое обеспечение на базе профессионального стандарта «Специалист по метрологии»
Метрологическое обеспечение на базе профессионального стандарта «Специалист по метрологии» Координатная плоскость. Рисуем координатами
Координатная плоскость. Рисуем координатами Треугольники. Решение задач
Треугольники. Решение задач Тема: Решение задач с помощью пропорции Автор: Яковлева Г.В. Учитель математики МОУ»СОШ№8»
Тема: Решение задач с помощью пропорции Автор: Яковлева Г.В. Учитель математики МОУ»СОШ№8»  Презентация по математике "Подготовка к ЕГЭ Задание В8" - скачать бесплатно
Презентация по математике "Подготовка к ЕГЭ Задание В8" - скачать бесплатно Пифагор и его теорема
Пифагор и его теорема Геометрия. Билет 15
Геометрия. Билет 15 Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Mediany_bissektrisy_i_vysoty_treugolnika
Mediany_bissektrisy_i_vysoty_treugolnika Математика профильный уровень. Тест №11
Математика профильный уровень. Тест №11 Предел функции. Пределы с неопределенностью вида и метод их решения
Предел функции. Пределы с неопределенностью вида и метод их решения Презентация по математике "Точки экстремума" - скачать
Презентация по математике "Точки экстремума" - скачать  Задачка по математике Прогулка
Задачка по математике Прогулка Стеценко Олеся 6 «А»
Стеценко Олеся 6 «А» Шифровка
Шифровка Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников Решение логических задач. Математика. 1,2 класс
Решение логических задач. Математика. 1,2 класс Занимательная математика
Занимательная математика Система организации вагонопотоков. План формирования групповых поездов. (Тема 7)
Система организации вагонопотоков. План формирования групповых поездов. (Тема 7) Объём. Объём прямоугольного параллелепипеда и куба
Объём. Объём прямоугольного параллелепипеда и куба Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Объем тела
Объем тела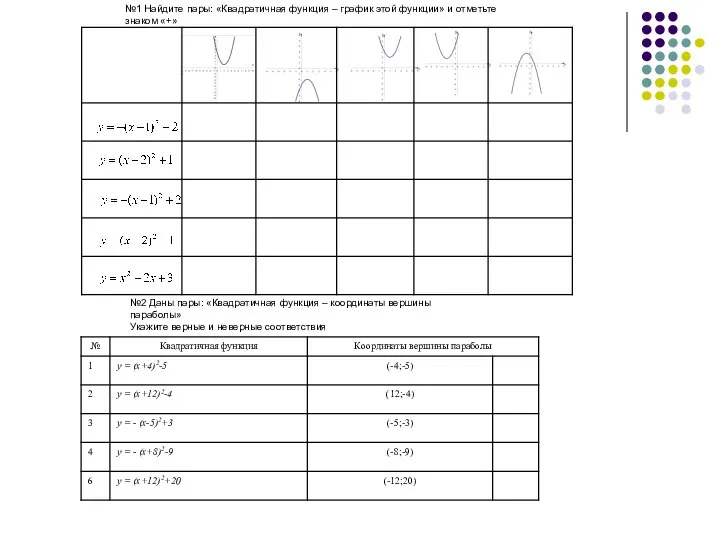 Функция у = а (х -x0) +y0
Функция у = а (х -x0) +y0 Параллелепипед построение
Параллелепипед построение Неполные квадратные уравнения. 8 класс
Неполные квадратные уравнения. 8 класс