Содержание
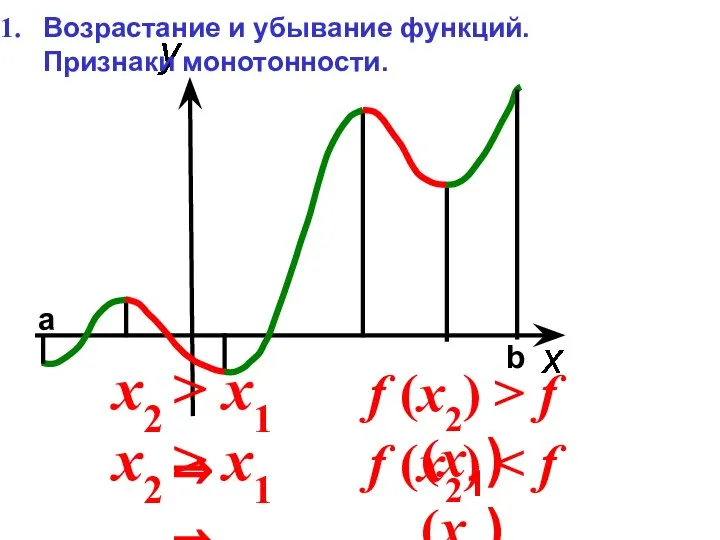
- 2. x2 > x1 ⇒ f (x2) > f (x1) x2 > x1 ⇒ f (x2) Возрастание
- 3. Признак возрастания функции. Для того, чтобы функция y=f(x) возраста-ла на промежутке, необходимо и доста-точно, чтобы производная
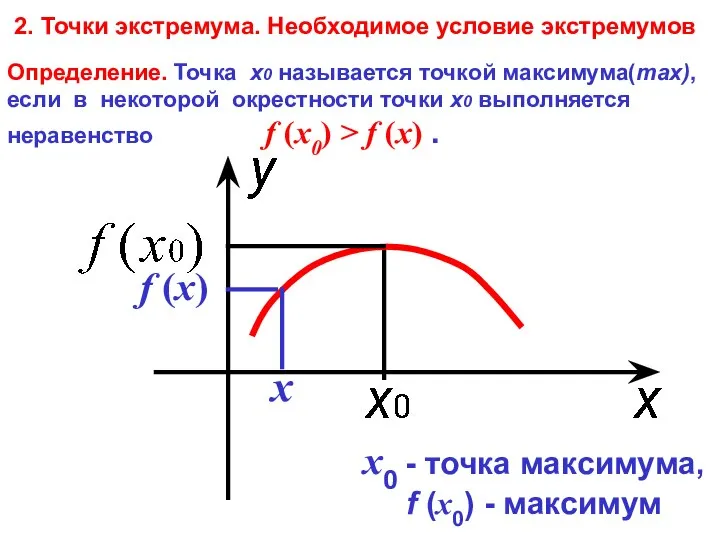
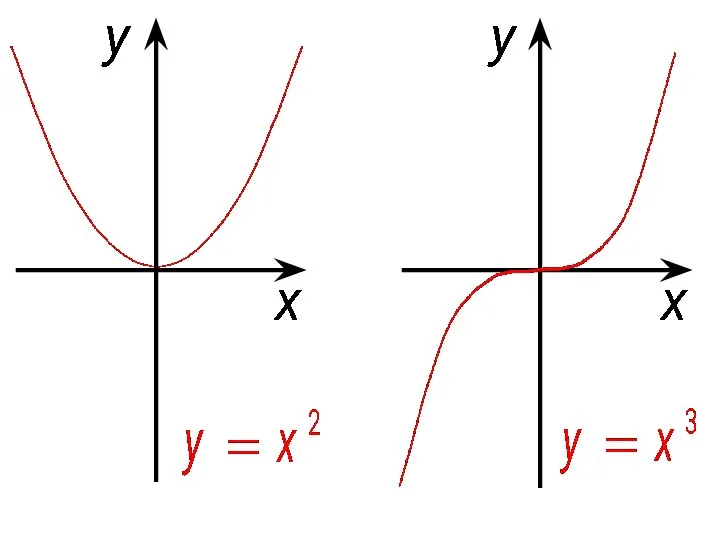
- 4. Определение. Точка х0 называется точкой максимума(max), если в некоторой окрестности точки х0 выполняется неравенство f (x0)
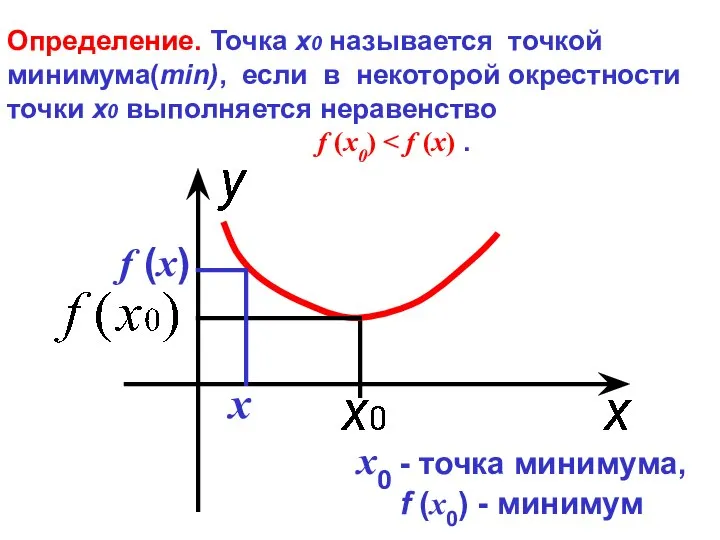
- 5. Определение. Точка х0 называется точкой минимума(min), если в некоторой окрестности точки х0 выполняется неравенство f (x0)
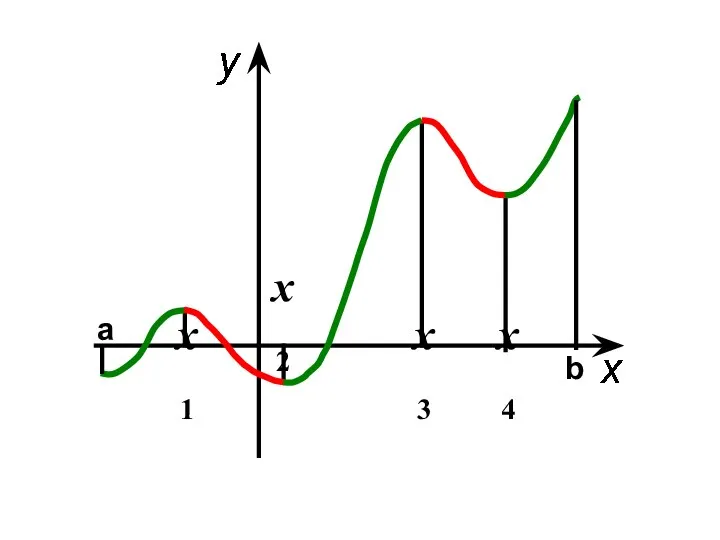
- 6. x1 x2 x3 x4
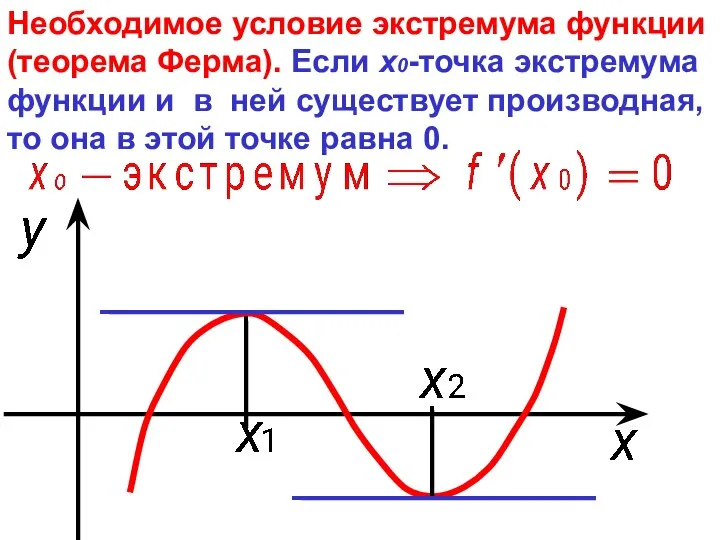
- 7. Необходимое условие экстремума функции (теорема Ферма). Если х0-точка экстремума функции и в ней существует производная, то
- 9. Теорема (1-е достаточное условие существования экстремума). Пусть x0 - критическая точка функции y=f(x) (т.е. или не
- 10. Схема исследования функции на монотонность и экстремумы. 1. Найти 2. Найти критические точки 1-го рода. (т.е.
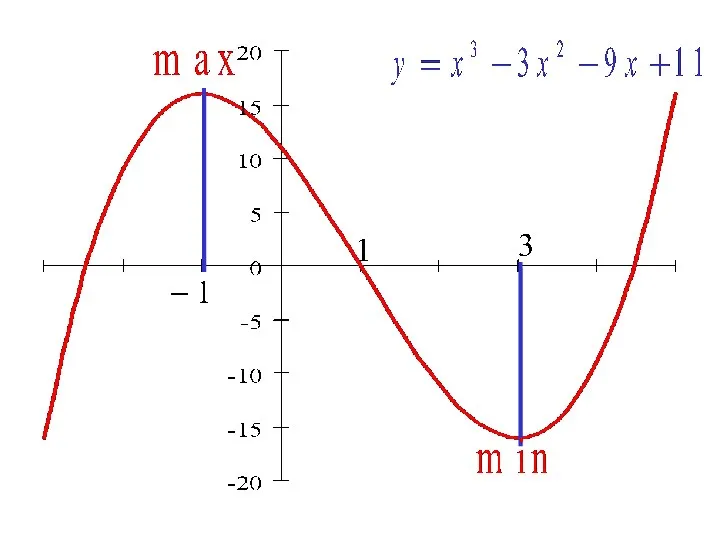
- 11. Пример. Исследовать функцию на монотонность, точки экстремума. -1 3 0 0 + - + Max 16
- 13. Исследование на экстремум с помощью производных высших порядков.
- 14. Теорема (2-е достаточное условие существования экстремума). Пусть x0 - критическая точка функции, т.е. или не существует.
- 15. Пример Функцию исследовать на точки экстремума по 2-му достаточному условию.
- 17. Скачать презентацию







 Задание на исследование функции с помощью производной
Задание на исследование функции с помощью производной Этапы расчета прогнозных значений методом двойного скользящего среднего
Этапы расчета прогнозных значений методом двойного скользящего среднего Комбинаторика
Комбинаторика Функция графигінің асимптоталары
Функция графигінің асимптоталары Составные задачи. Урок № 104
Составные задачи. Урок № 104 Методика изучения статистических характеристик в курсе математики основной школы
Методика изучения статистических характеристик в курсе математики основной школы Действия с одночленами
Действия с одночленами Площади фигур. Теорема Пифагора
Площади фигур. Теорема Пифагора Устные приемы вычитания вида 35-7
Устные приемы вычитания вида 35-7 Сложение и вычитание дробей с разными знаменателями. (6 класс)
Сложение и вычитание дробей с разными знаменателями. (6 класс) Обратная матрица: определение, необходимые условия существования
Обратная матрица: определение, необходимые условия существования Движение_в_противоположном_направлении
Движение_в_противоположном_направлении Геометрия и ландшафтный дизайн
Геометрия и ландшафтный дизайн Понятие вектора
Понятие вектора Аттестационная работа. Программа внеурочной деятельности по математике «В мире чисел и задач». (7 класс)
Аттестационная работа. Программа внеурочной деятельности по математике «В мире чисел и задач». (7 класс) Час занимательной математики. 5 класс
Час занимательной математики. 5 класс Точность коэффициентов множественной регрессии
Точность коэффициентов множественной регрессии Своя игра по математике
Своя игра по математике Методика обучения решению сюжетных задач в курсе математики 5-6 классов
Методика обучения решению сюжетных задач в курсе математики 5-6 классов Измерительные работы
Измерительные работы Корень уравнения
Корень уравнения Задачи по геометрии (6-7)
Задачи по геометрии (6-7) Работа с циркулем
Работа с циркулем Математические основы анализа свойств систем и наблюдения их состояния (лекция № 17)
Математические основы анализа свойств систем и наблюдения их состояния (лекция № 17) Решение задач на вычисление площади поверхности призмы
Решение задач на вычисление площади поверхности призмы Свойство сторон прямоугольника
Свойство сторон прямоугольника Практикум по решению задачи №20 (базовый уровень). ЕГЭ
Практикум по решению задачи №20 (базовый уровень). ЕГЭ Эндоскопическая хирургия в лечении миомы матки
Эндоскопическая хирургия в лечении миомы матки