Содержание
- 2. Понятие неопределенного интеграла В дифференциальном исчислении решается задача: по данной функции f(x) найти ее производную. Интегральное
- 3. Операция нахождения неопределенного интеграла от функции называется называется интегрированием этой функции. Множество всех первообразных функций F(x)
- 4. Свойства неопределенного интеграла Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная от неопределенного интеграла равна
- 5. Неопределенный интеграл от суммы (разности) конечного числа непрерывных функций равен сумме (разности) интегралов: Инвариантность формулы интегрирования:
- 6. Таблица интегралов
- 8. Непосредственное интегрирование Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств
- 9. Введение части функции под знак дифференциала. При сведении данного интеграла к табличному часто применяются следующие преобразования
- 11. Метод интегрирования подстановкой (заменой переменной) Метод интегрирования подстановкой заключается во введении новой переменной интегрирования. Пусть требуется
- 14. Метод интегрирования по частям Интегрируя это равенство, получим: Интегрирование по частям состоит в том, что подынтегральное
- 15. Интегралы вида: где: P(x) – многочлен. Удобно положить u = P(x), dv – остальные сомножители. Типы
- 17. Метод интегрирования по частям
- 19. Скачать презентацию











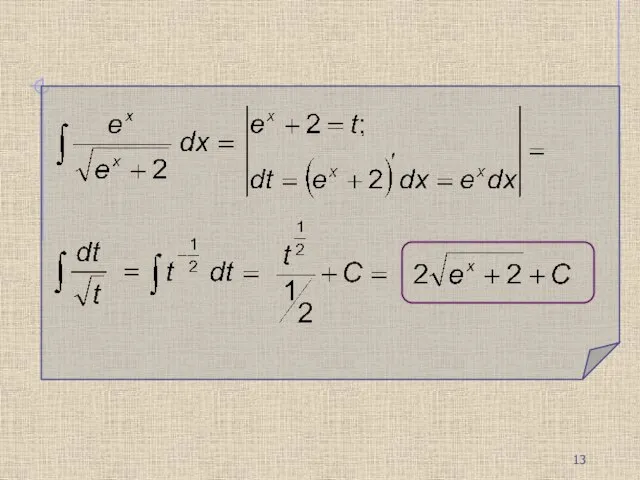




 Логические высказывания
Логические высказывания Нахождение целого по части
Нахождение целого по части Призма в задачах ЕГЭ
Призма в задачах ЕГЭ Геометрический смысл двойного интеграла
Геометрический смысл двойного интеграла Функционально-графические методы решения комбинированных уравнений. 11 класс
Функционально-графические методы решения комбинированных уравнений. 11 класс Интерактивный тренажёр по математике + окружающий мир, Орёл - фотограф. 4 класс
Интерактивный тренажёр по математике + окружающий мир, Орёл - фотограф. 4 класс Заполнение угла и окружности
Заполнение угла и окружности Умножение 7, 8, 9, 10
Умножение 7, 8, 9, 10 Функції та їх графіки
Функції та їх графіки Морское путешествие
Морское путешествие Основные теоремы о пределах. Способы вычисления пределов функций. (Семинар 5)
Основные теоремы о пределах. Способы вычисления пределов функций. (Семинар 5) Логарифмы. Логарифмическая функция. 11 класс
Логарифмы. Логарифмическая функция. 11 класс Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Площадь треугольника
Площадь треугольника Презентация по математике "Деление числа с остатком. Обобщение" - скачать
Презентация по математике "Деление числа с остатком. Обобщение" - скачать  Графики и диаграммы. Задания
Графики и диаграммы. Задания Циклоидальные кривые
Циклоидальные кривые Решение неравенств с одной переменной
Решение неравенств с одной переменной Интерактивный тест по математике. Решаем задачи с Буратино (3 класс)
Интерактивный тест по математике. Решаем задачи с Буратино (3 класс) Линейная функция. Построение графиков функций, аналитическое выражение которых содержит знак абсолютной величины
Линейная функция. Построение графиков функций, аналитическое выражение которых содержит знак абсолютной величины Преобразование выражения Asinx+Bcosx к виду Csin(x+t)
Преобразование выражения Asinx+Bcosx к виду Csin(x+t) Решение задач на перебор всех вариантов (комбинаторные)
Решение задач на перебор всех вариантов (комбинаторные) Решение логических задач с помощью кругов Эйлера Занятие 1
Решение логических задач с помощью кругов Эйлера Занятие 1 Таблицы. Геометрия
Таблицы. Геометрия Графический способ решения уравнений. Урок 95
Графический способ решения уравнений. Урок 95 Презентация по математике "Арифметический корень натуральной степени" - скачать
Презентация по математике "Арифметический корень натуральной степени" - скачать  Арифметический квадратный корень
Арифметический квадратный корень Презентация по математике "Тест по математике за первое полугодие для 1 класса" - скачать
Презентация по математике "Тест по математике за первое полугодие для 1 класса" - скачать