Содержание
- 2. Существует ряд задач на графах, в которых требуется найти маршрут, который содержит все вершины или ребра
- 3. Одна из задач заключается в том, чтобы обойти все вершины графа и в каждой из них
- 4. 3.1. Поиск в ширину (breadth-first search, BFS) 1. Поиск начинается с некоторой фиксированной вершины s. 2.
- 8. 3.1. Эйлеровы цепи и циклы
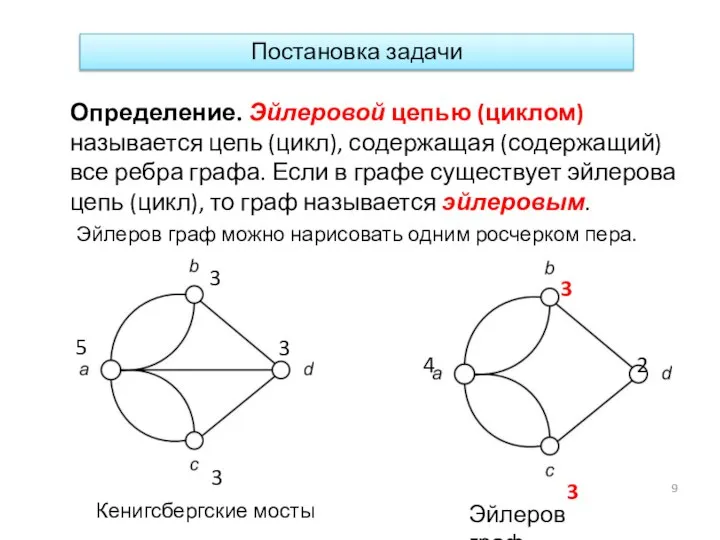
- 9. Определение. Эйлеровой цепью (циклом) называется цепь (цикл), содержащая (содержащий) все ребра графа. Если в графе существует
- 10. Теорема. Эйлерова цепь (цикл) существует тогда и только тогда, когда число вершин с нечетной валентностью равно
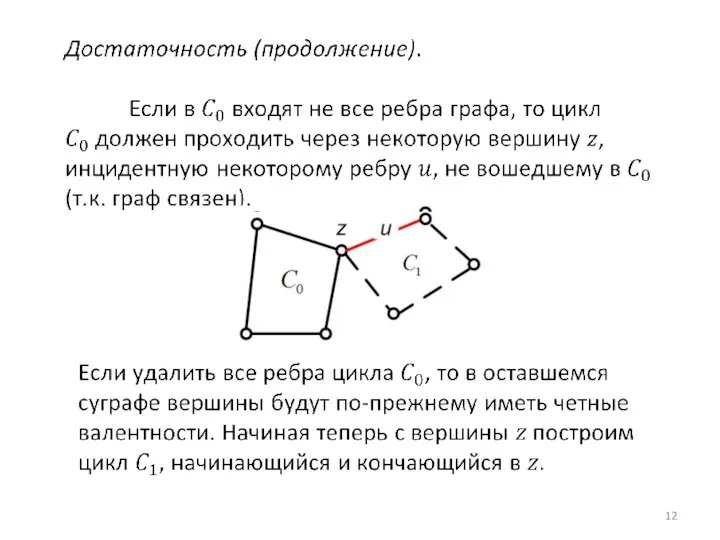
- 14. На этом доказательстве основан алгоритм нахождения эйлеровой цепи.
- 15. В 1736 г. Л.Эйлер опубликовал эту теорему, носящую в литературе его имя, без доказательства достаточности. Фрагмент
- 16. Алгоритм Хирхольцера В 1873 г. вышла статья немецкого математика К. Хирхольцера (Carl Hierholzer, 1840 – 1871),
- 17. Алгоритм Хирхольцера выполняется в точном соответствии с доказательством достаточности теоремы Эйлера. Рассмотрим обыкновенный связный граф без
- 18. Шаг 0. Выбрать начальную вершину s; /* Поместить s в C */ Шаг 1. Выбрать в
- 19. Шаг 2. /* Поиск цикла */ – /* выбрать не пройденное ребро*/. /* Добавить y в
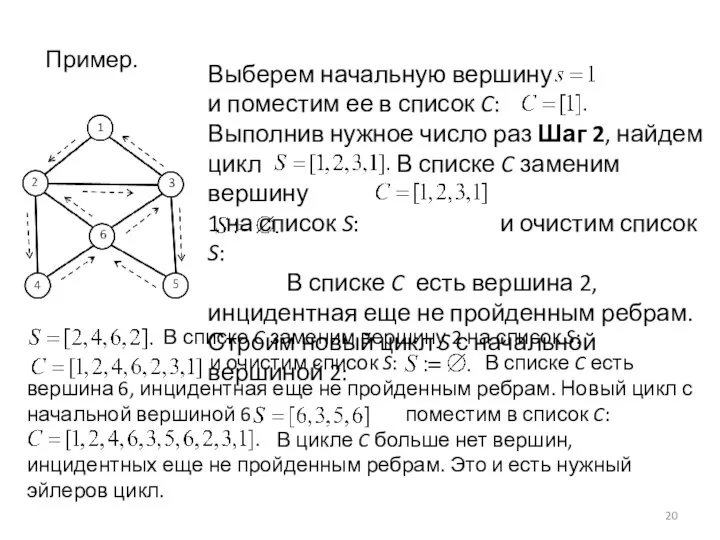
- 20. Пример. Выберем начальную вершину и поместим ее в список C: Выполнив нужное число раз Шаг 2,
- 21. На поиск вершин, инцидентных еще не пройденным ребрам, понадобится самое большее n просмотров; на включение ребер
- 22. Алгоритм 2 [Липский]. Задан обыкновенный связный граф без вершин с нечетной степенью. Граф задан списками смежности
- 23. Шаг 1. если то {Выход – C искомый эйлеров цикл}. /* Поиск цикла*/ /* := верхний
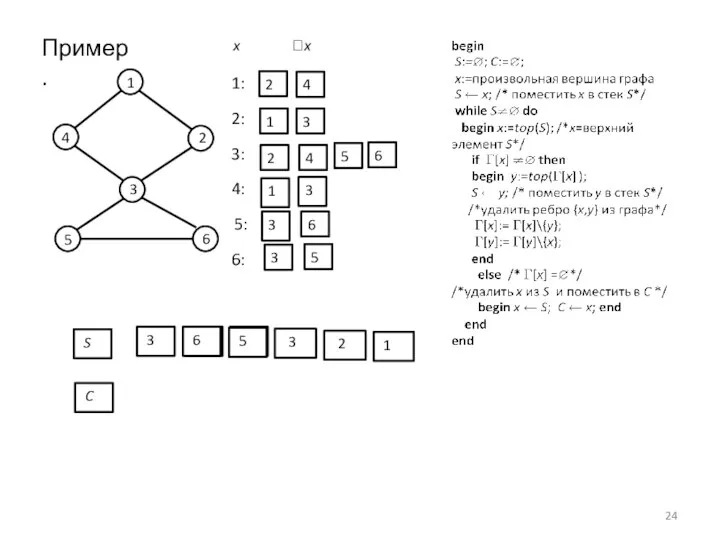
- 24. Пример. 3 1 4 2 5 6 3 2 4 1 3 2 4 6 1
- 26. (для всех вершин, кроме s и t, полувалентности исхода и полувалентности захода равны; для вершины s
- 27. Задача китайского почтальона В графе с неотрицательными весами ребер найти циклический маршрут наименьшей длины, проходящий через
- 28. 3.1. Гамильтоновы цепи и циклы
- 29. Постановка задачи Определение. Гамильтоновой цепью (циклом) графа называется простая цепь (простой цикл), содержащая (содержащий) все вершины
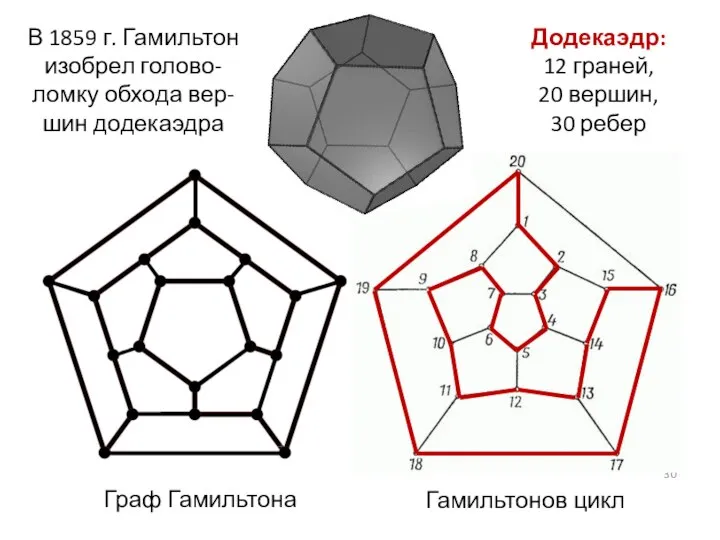
- 30. Граф Гамильтона Додекаэдр: 12 граней, 20 вершин, 30 ребер Гамильтонов цикл В 1859 г. Гамильтон изобрел
- 31. Мы рассмотрим два простейших переборных алгоритма поиска гамильтоновой цепи (цикла), пригодных для графов малой размерности: поиск
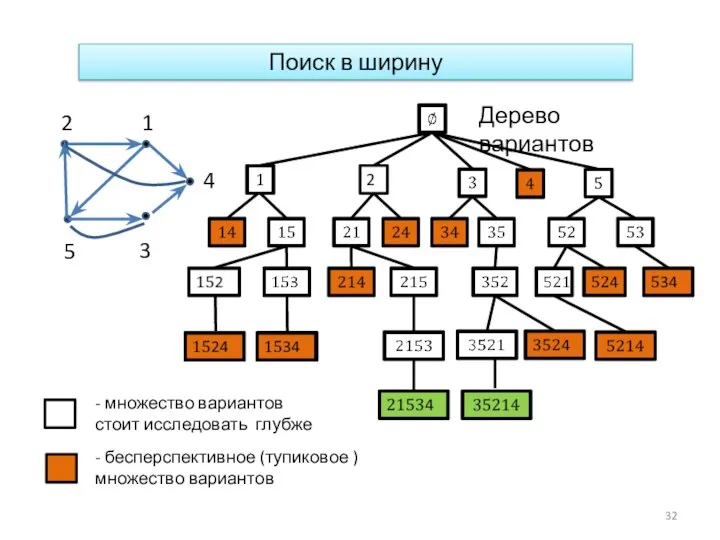
- 32. Поиск в ширину 2 - бесперспективное (тупиковое ) множество вариантов - множество вариантов стоит исследовать глубже
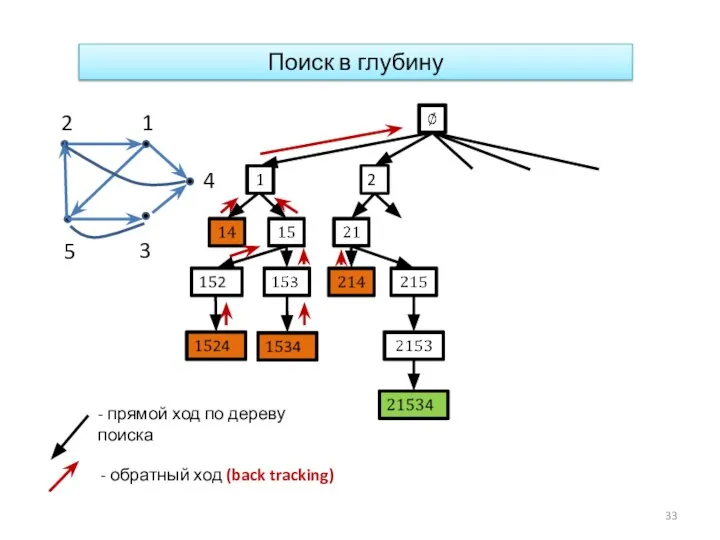
- 33. Поиск в глубину 2 - прямой ход по дереву поиска - обратный ход (back tracking)
- 34. Задача коммивояжера Задача коммивояжера (travelling seller problem, TSP) формулируется следующим образом: во взвешенном графе (обычно –
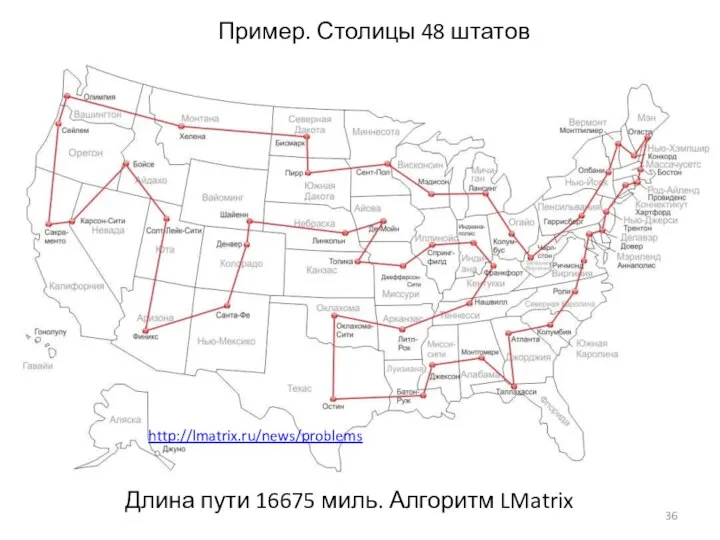
- 36. Пример. Столицы 48 штатов Длина пути 16675 миль. Алгоритм LMatrix http://lmatrix.ru/news/problems
- 38. Скачать презентацию

















![Алгоритм 2 [Липский]. Задан обыкновенный связный граф без вершин с нечетной](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/687667/slide-21.jpg)









 Задания для устного счёта по теме «Обыкновенные дроби» Артамонова Л.В., Учитель математики МКОУ «Москаленский лицей»
Задания для устного счёта по теме «Обыкновенные дроби» Артамонова Л.В., Учитель математики МКОУ «Москаленский лицей»  Решение систем неравенств
Решение систем неравенств Преобразование выражений, содержащих квадратные корни Учитель математики МБОУ гимназии № 82 г. Краснодара Чернова Татьяна Викто
Преобразование выражений, содержащих квадратные корни Учитель математики МБОУ гимназии № 82 г. Краснодара Чернова Татьяна Викто Изучение таблицы умножения в разных странах
Изучение таблицы умножения в разных странах Нахождение числа по его дроби Автор: учитель математики Мариупольской общеобразовательной школы І-ІІІ ступеней № 41 Белецкая
Нахождение числа по его дроби Автор: учитель математики Мариупольской общеобразовательной школы І-ІІІ ступеней № 41 Белецкая Элементы аналитической геометрии
Элементы аналитической геометрии Углы и отрезки, связанные с окружностью. 10 класс
Углы и отрезки, связанные с окружностью. 10 класс Презентация на тему Умножение одночлена на многочлен
Презентация на тему Умножение одночлена на многочлен  Равнобедренный треугольник
Равнобедренный треугольник Понятие предела числовой последовательности. Предел функции в точке и на бесконечности. Теоремы о пределах функции
Понятие предела числовой последовательности. Предел функции в точке и на бесконечности. Теоремы о пределах функции Пространство в современной физике
Пространство в современной физике Функции y = tg x, y = ctg x, их свойства и графики
Функции y = tg x, y = ctg x, их свойства и графики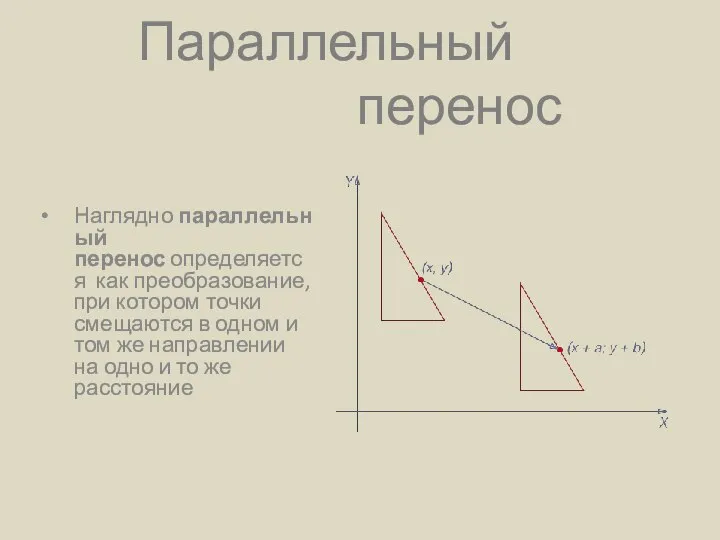 Параллельный перенос
Параллельный перенос Розкриття дужок. Зведення подібних доданків
Розкриття дужок. Зведення подібних доданків  Новый год и правильные многогранники
Новый год и правильные многогранники Основные понятия теории вероятностей
Основные понятия теории вероятностей Перпендикулярные прямые
Перпендикулярные прямые 20161212_ot_evklida_do_lobachevskogo
20161212_ot_evklida_do_lobachevskogo Решение рациональных уравнений
Решение рациональных уравнений Логіка предикатів. (Лекция 3)
Логіка предикатів. (Лекция 3) Формула включений и исключений. Беспорядки. (Лекция 12)
Формула включений и исключений. Беспорядки. (Лекция 12) Математическая викторина
Математическая викторина Деление числа в данном отношении
Деление числа в данном отношении Формализованные методы прогнозирования
Формализованные методы прогнозирования Проекцияларды өзгерту әдістері
Проекцияларды өзгерту әдістері Основы теории множеств
Основы теории множеств Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Ломаные линии и многоугольники
Ломаные линии и многоугольники