Описанная и вписанная окружность треугольника

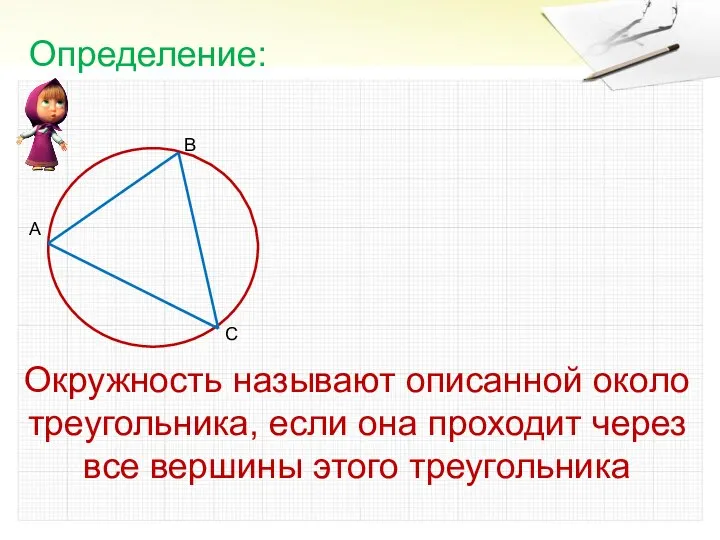
Окружность называют описанной около треугольника, если она проходит через все вершины

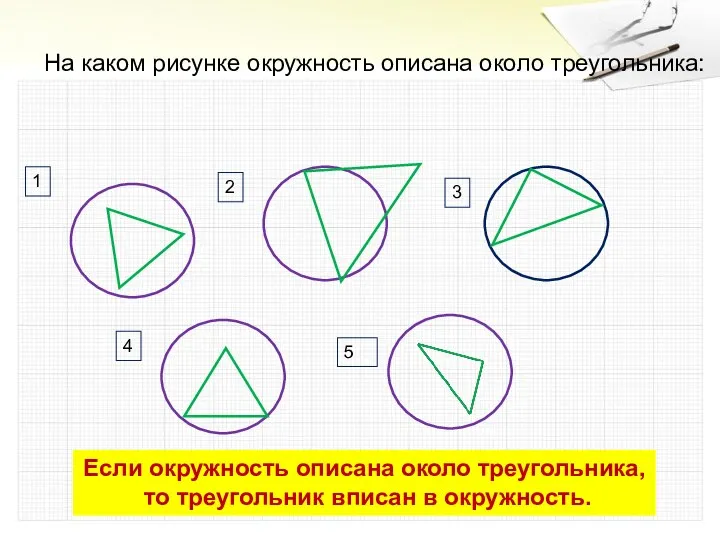
На каком рисунке окружность описана около треугольника:

1

2

3

4

5

Если окружность описана около треугольника,

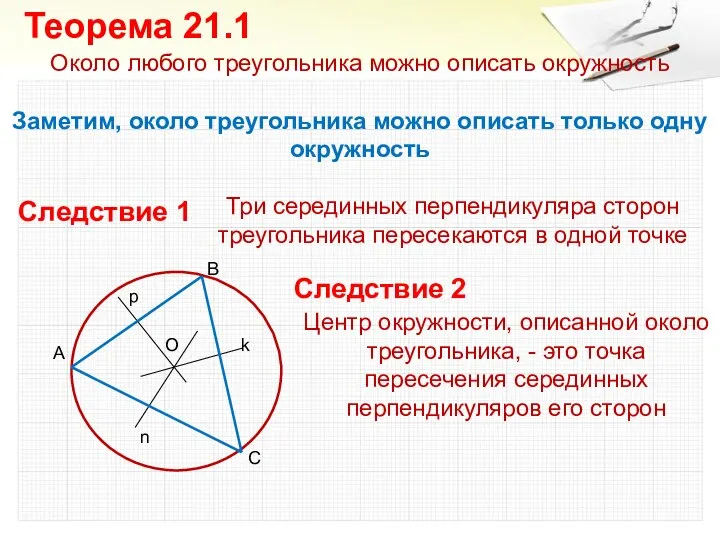
Около любого треугольника можно описать окружность
Заметим, около треугольника можно описать только

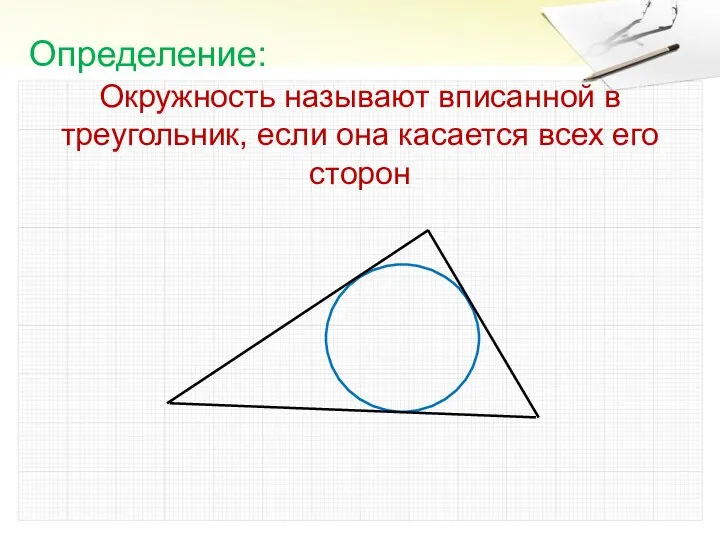
Окружность называют вписанной в треугольник, если она касается всех его сторон

Определение:

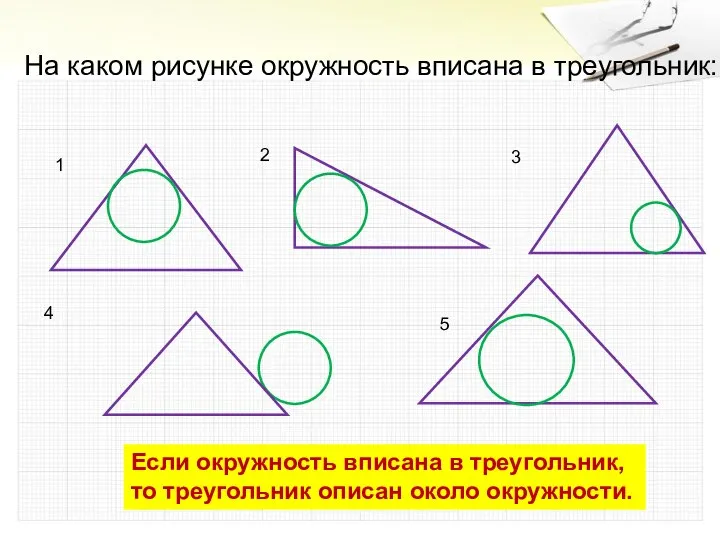
На каком рисунке окружность вписана в треугольник:

1

3

4

Если окружность вписана в треугольник,

Заметим, в треугольник можно вписать окружность,
и притом только одну.

О

С1

А1

В1

В

r

Биссектрисы углов треугольника пересекаются в одной точке

Следствие 1

Следствие 2

Центр окружности, вписанной

Радиус окружности вписанной в прямоугольный треугольник, определяется по формуле

где r

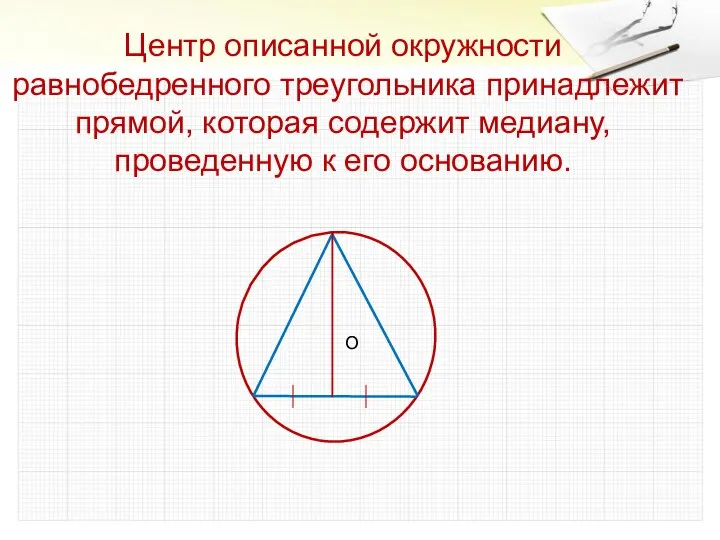
Центр описанной окружности равнобедренного треугольника принадлежит прямой, которая содержит медиану, проведенную

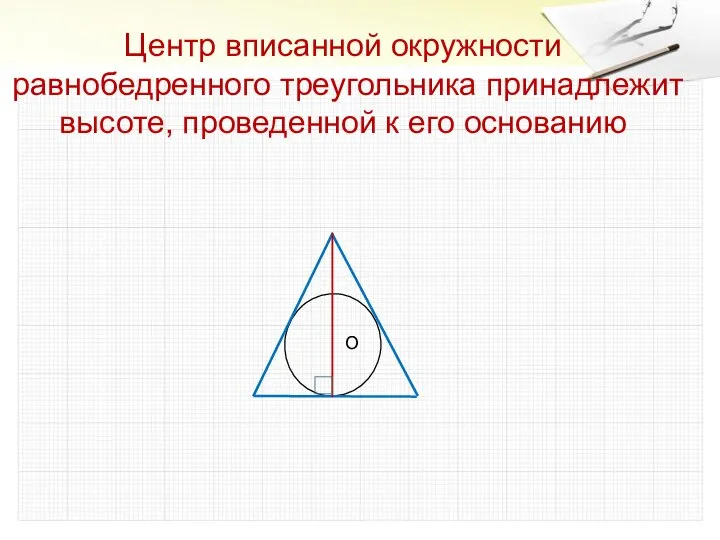
Центр вписанной окружности равнобедренного треугольника принадлежит высоте, проведенной к его основанию

О

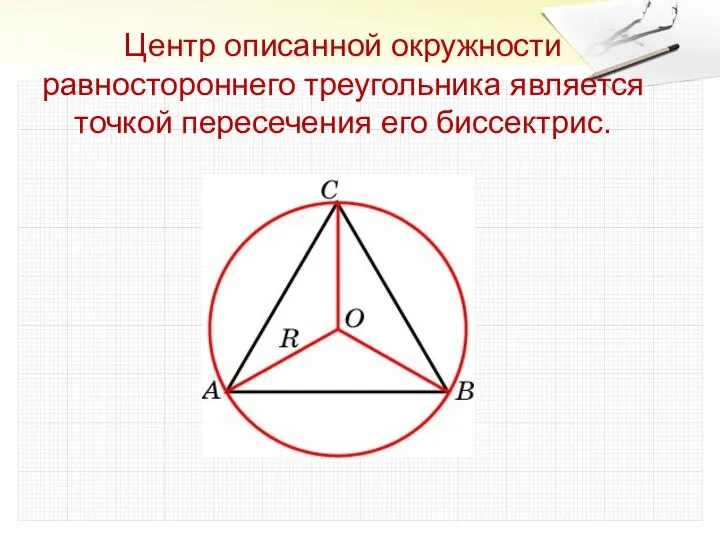
Центр описанной окружности равностороннего треугольника является точкой пересечения его биссектрис.

Если центр окружности, описанной около треугольника принадлежит его стороне, то треугольник

Касательная к окружности

Определение: Прямая, имеющая с окружностью только одну общую точку,

Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

m

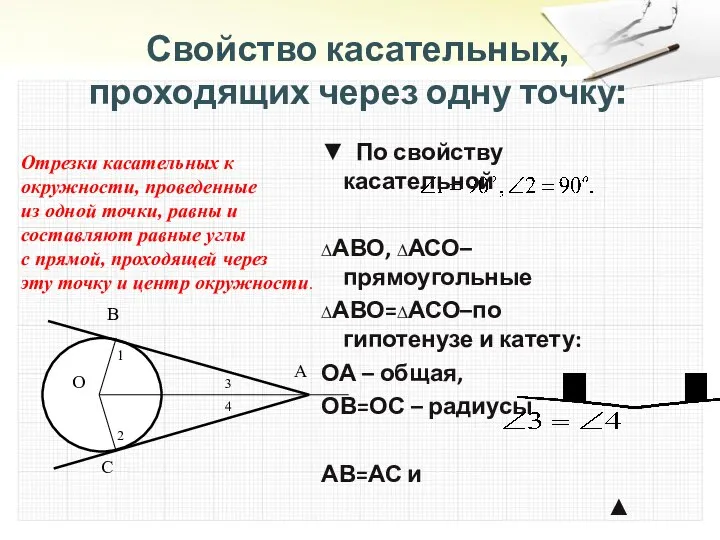
Свойство касательных, проходящих через одну точку:

▼ По свойству касательной
∆АВО, ∆АСО–прямоугольные
∆АВО=∆АСО–по

Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и

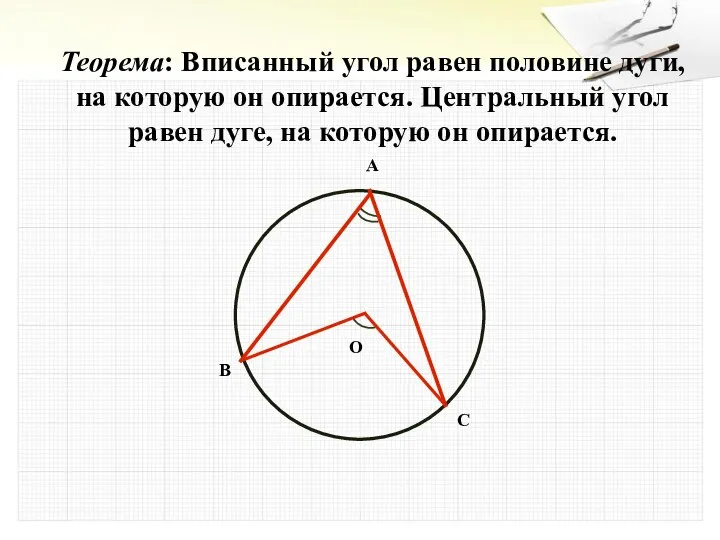
Теорема: Вписанный угол равен половине дуги, на которую он опирается. Центральный

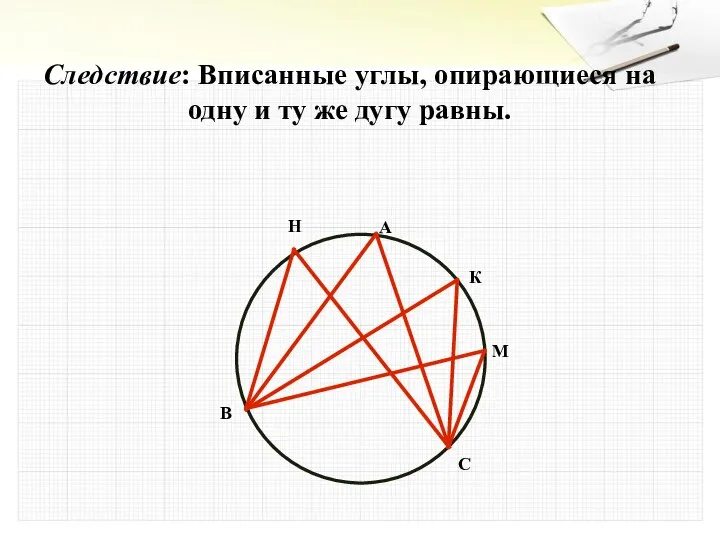
Следствие: Вписанные углы, опирающиеся на одну и ту же дугу равны.

Следствие: Вписанный угол, опирающийся на
диаметр - прямой.

А

В

С

.

О

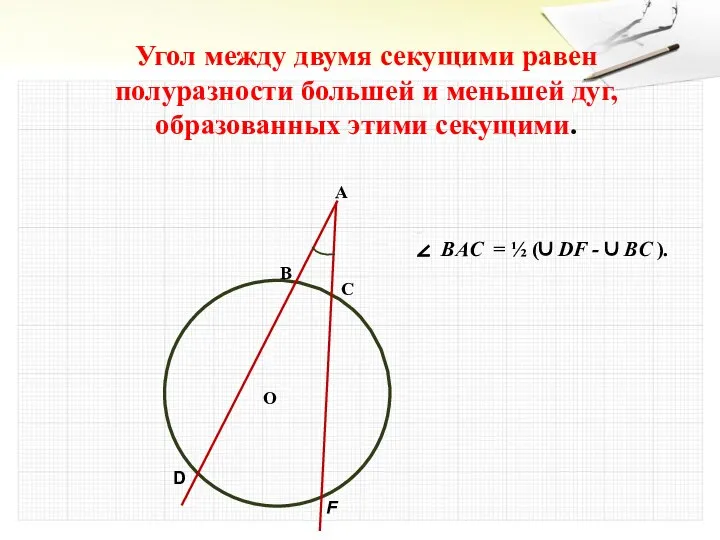
А

О

С

В

D

F

Угол между двумя секущими равен
полуразности большей и меньшей дуг,
образованных

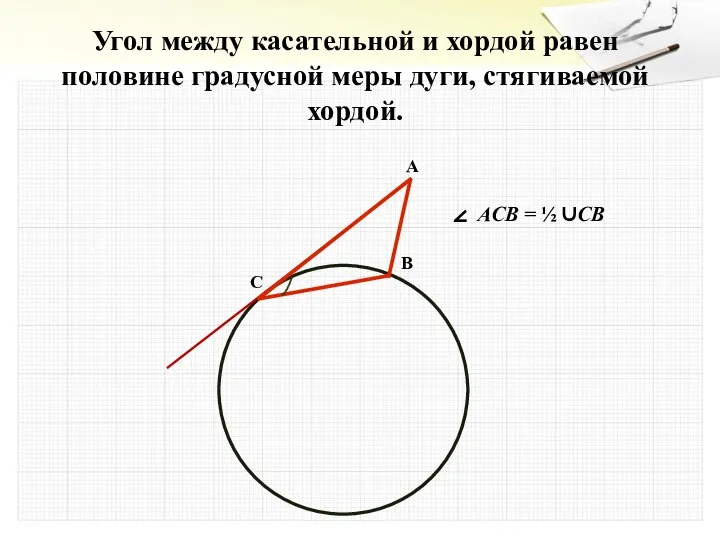
Угол между касательной и хордой равен половине градусной меры дуги, стягиваемой

Теорема: Если две хорды окружности пересекаются, то произведение отрезков одной хорды

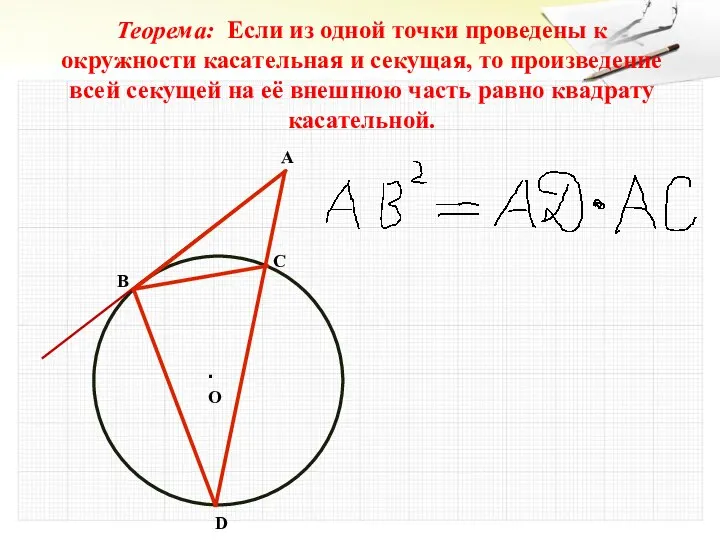
Теорема: Если из одной точки проведены к окружности касательная и секущая,

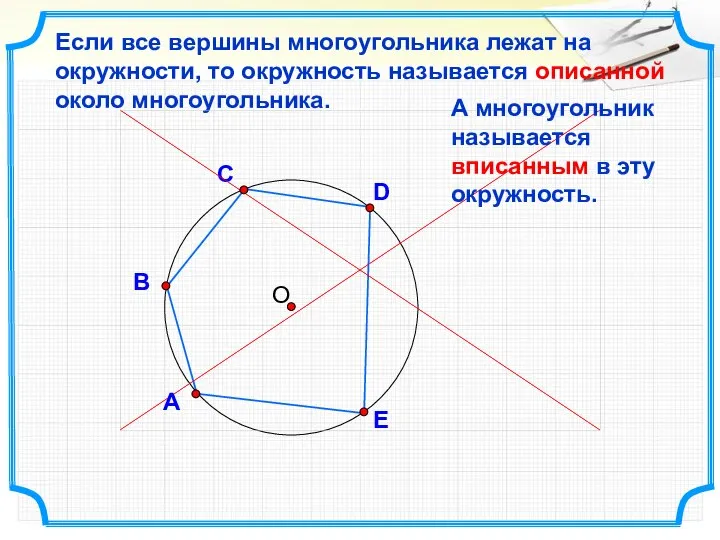
D

В

С

Если все вершины многоугольника лежат на окружности, то окружность называется описанной

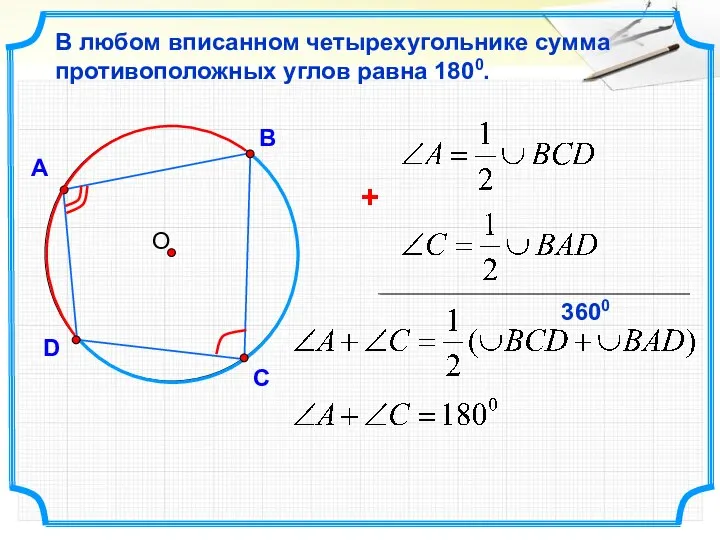
А

В

D

В любом вписанном четырехугольнике сумма противоположных углов равна 1800.

С

3600