Содержание
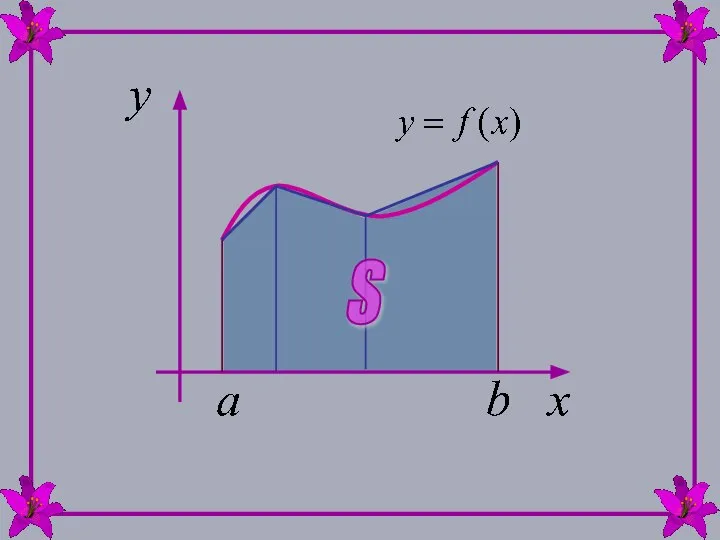
- 2. 14.1. ПОНЯТИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА Пусть на отрезке [a,b] задана неотрицательная функция y=f(x). Требуется найти площадь криволинейной
- 3. Фигура под ломаной состоит из трапеций и ее площадь равна сумме площадей всех трапеций: Причем, площадь
- 4. S
- 5. За искомую площадь под кривой берут предел площади под ломаной при условии, что ломаная неограниченно приближается
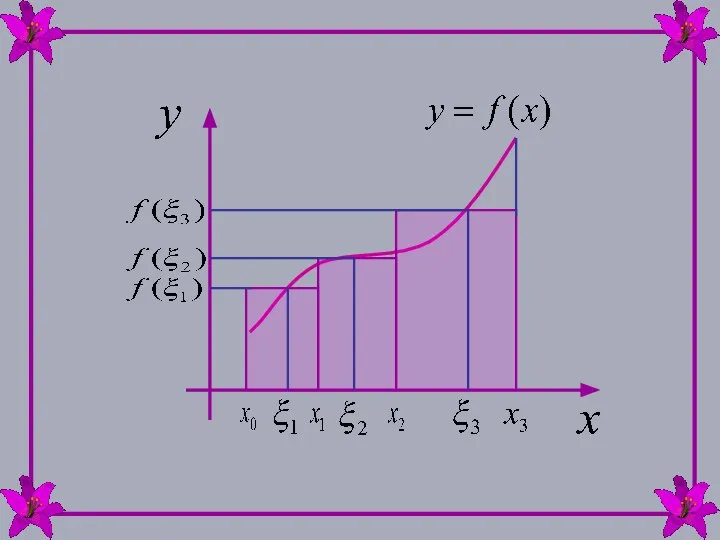
- 6. Сумму вида называют интегральной суммой для функции y=f(x) на отрезке [a,b] .
- 7. Интегральная сумма зависит от способа разбиения отрезка и выбора точек ξi Каждое отдельное слагаемое в интегральной
- 9. Наибольший из отрезков разбиения обозначим как Вся интегральная сумма будет равна
- 10. Если существует конечный предел интегральной суммы при не зависящий от способа разбиения отрезка [a,b] и выбора
- 11. Функция y=f(x) называется интегрируемой на отрезке [a,b]. Числа a и b называются нижним и верхним пределом,
- 12. Неопределенный интеграл есть семейство функций, а определенный интеграл есть определенное число. По определению предполагается, что а
- 13. С учетом этого несущественно, какой предел больше или меньше. Если а = b, то
- 14. Необходимое условие существования определенного интеграла 14.2. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА Интегрируемая на отрезке [a,b] функция y=f(x) ограничена
- 15. Достаточное условие существования определенного интеграла Если на отрезке [a,b] функция y=f(x) непрерывна, то она интегрируема на
- 16. Свойства определенного интеграла 1 Постоянный множитель можно выносить за знак определенного интеграла.
- 17. 2 Определенный интеграл от алгебраической суммы (разности) двух функций равен сумме (разности) интегралов от этих функций.
- 18. 3 Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов по
- 19. Геометрически это означает, что если a
- 20. S S S
- 21. 4 Если на [a,b], где a то
- 22. Следствие. Пусть на [a,b], где a где m и M некоторые числа. Тогда
- 23. 6 Если на [a,b] функция y=f(x) неотрицательна, то площадь под этой кривой численно равна определенному интегралу
- 24. Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная этой функции на [a,b],
- 25. Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: 1 Находится некоторая первообразная F(x)
- 26. 1 Вычислить определенный интеграл Примеры. Решение.
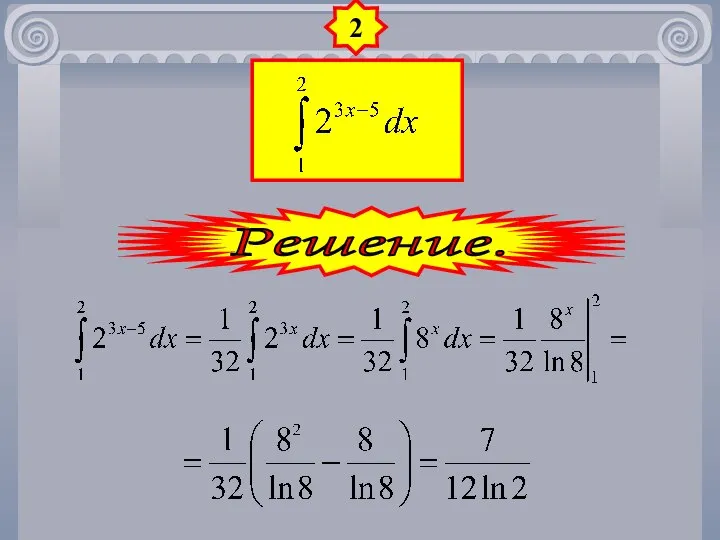
- 27. 2 Решение.
- 28. Рассмотрим правило замены переменной и интегрирование по частям в определенном интеграле. Сформулируем две теоремы. 14.4. ЗАМЕНА
- 29. Пусть функция φ(t) имеет непрерывную производную на [α,β], где φ(α)=a, φ(β)=b и функция f(x) непрерывна в
- 30. Как и в случае неопределенного интеграла замена переменной во многих случаях позволяет свести интеграл к табличному.
- 31. На практике, выполняя замену переменной, часто указывают выражение новой переменной через старую. В этом случае нахождение
- 32. Вычислить определенный интеграл Пример.
- 33. Решение:
- 34. Пусть функции u=u(x) и v=v(x) имеют непрерывные производные на [α,β], тогда где Теорема 2.
- 35. Вычислить определенный интеграл Пример.
- 37. Скачать презентацию
![14.1. ПОНЯТИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА Пусть на отрезке [a,b] задана неотрицательная функция](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/633749/slide-1.jpg)


![Сумму вида называют интегральной суммой для функции y=f(x) на отрезке [a,b] .](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/633749/slide-5.jpg)



![Функция y=f(x) называется интегрируемой на отрезке [a,b]. Числа a и b](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/633749/slide-10.jpg)



![Достаточное условие существования определенного интеграла Если на отрезке [a,b] функция y=f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/633749/slide-14.jpg)




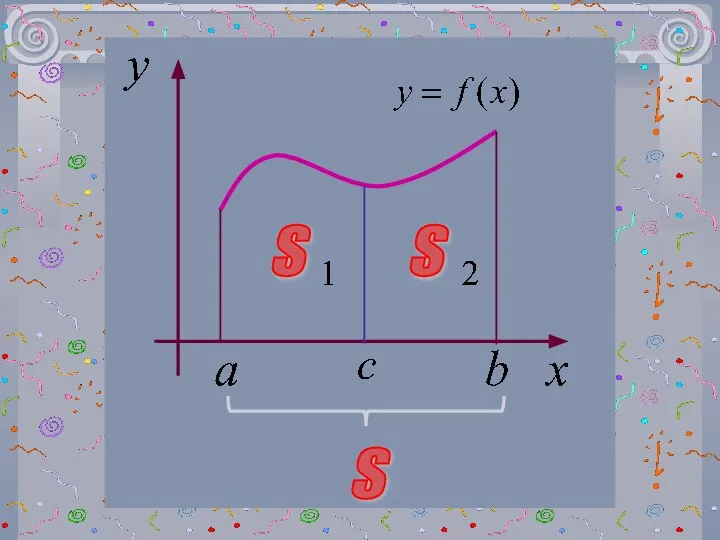
![4 Если на [a,b], где a то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/633749/slide-20.jpg)
![Следствие. Пусть на [a,b], где a где m и M некоторые числа. Тогда](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/633749/slide-21.jpg)
![6 Если на [a,b] функция y=f(x) неотрицательна, то площадь под этой](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/633749/slide-22.jpg)
![Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – любая](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/633749/slide-23.jpg)



![Пусть функция φ(t) имеет непрерывную производную на [α,β], где φ(α)=a, φ(β)=b](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/633749/slide-28.jpg)




![Пусть функции u=u(x) и v=v(x) имеют непрерывные производные на [α,β], тогда где Теорема 2.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/633749/slide-33.jpg)

 Площади различных геометрических фигур
Площади различных геометрических фигур Системы компьютерной алгебры. Maple, mathematica, derive
Системы компьютерной алгебры. Maple, mathematica, derive Вирішення задач аналізу СРІ з використанням математичного апарата марківських процесів
Вирішення задач аналізу СРІ з використанням математичного апарата марківських процесів Деление положительных и отрицательных чисел
Деление положительных и отрицательных чисел Великолепный часослов герцога Беррийского. Математика в каждом
Великолепный часослов герцога Беррийского. Математика в каждом Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки. Сумма двух векторов
Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки. Сумма двух векторов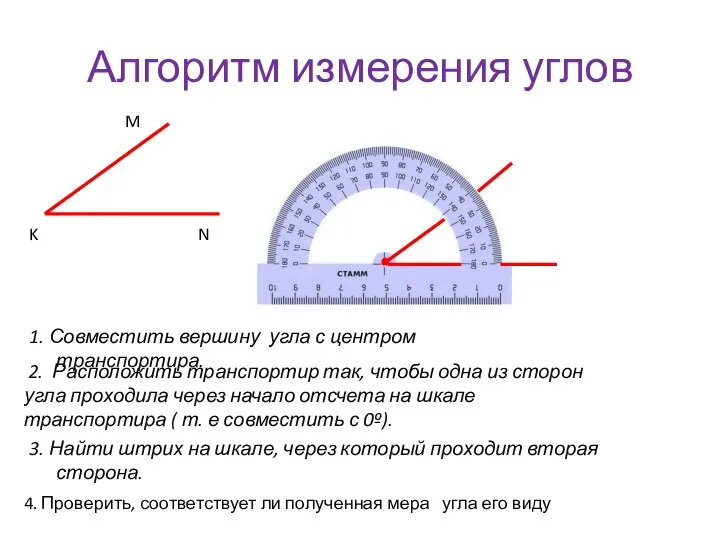 Алгоритм измерения углов
Алгоритм измерения углов Тест по теме: "Призма". Часть 2. Вариант 1
Тест по теме: "Призма". Часть 2. Вариант 1 Основы индуктивного подхода. Метод математической индукции
Основы индуктивного подхода. Метод математической индукции Объём прямоугольного параллелепипеда. Решение задач
Объём прямоугольного параллелепипеда. Решение задач Углы, связанные с окружностью. Геометрия, 8 класс
Углы, связанные с окружностью. Геометрия, 8 класс Решение задач на совместную работу
Решение задач на совместную работу Модели эксплуатации на основе метода динамики средних
Модели эксплуатации на основе метода динамики средних Графический метод решения уравнений. Задания для устного счета
Графический метод решения уравнений. Задания для устного счета Деление двузначного числа на однозначное
Деление двузначного числа на однозначное Отношения. Бинарные отношения и их свойства
Отношения. Бинарные отношения и их свойства Пирамида. Элементы пирамиды
Пирамида. Элементы пирамиды Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Числовые и алгебраические выражения
Числовые и алгебраические выражения Презентация на тему Решение задач на пропорциональное деление
Презентация на тему Решение задач на пропорциональное деление  Вектор на плоскости
Вектор на плоскости Перпендикулярные прямые
Перпендикулярные прямые Решение геометрических задач. Памятка по решению геометрических задач
Решение геометрических задач. Памятка по решению геометрических задач Линейная функция у=кх
Линейная функция у=кх Решение задач по геометрии
Решение задач по геометрии Презентация на тему Теорема Виета
Презентация на тему Теорема Виета  Корень n-ой степени и его свойства
Корень n-ой степени и его свойства Презентация на тему Логарифмическая функция
Презентация на тему Логарифмическая функция