Содержание
- 2. Задача о вычислении площади криволинейной трапеции. Пусть f(x) - непрерывная на [ a, b ] функция.
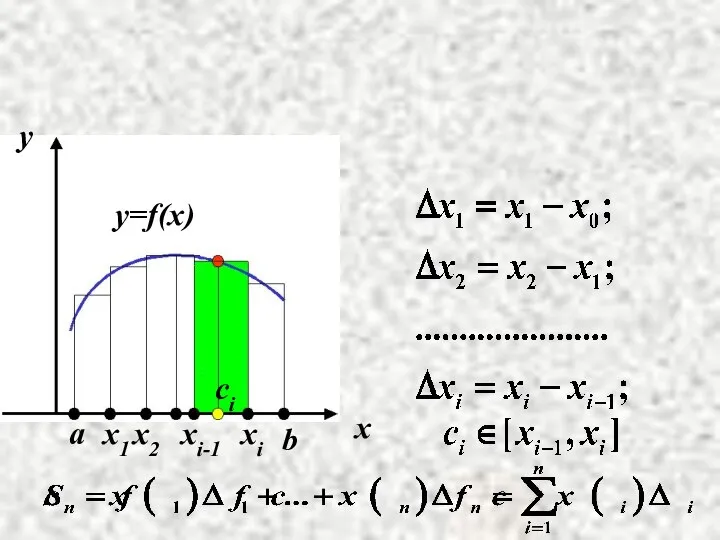
- 3. a b y=f(x) ci
- 4. Площадь криволинейной трапеции будет равна приближённо сумме площадей прямоугольников:
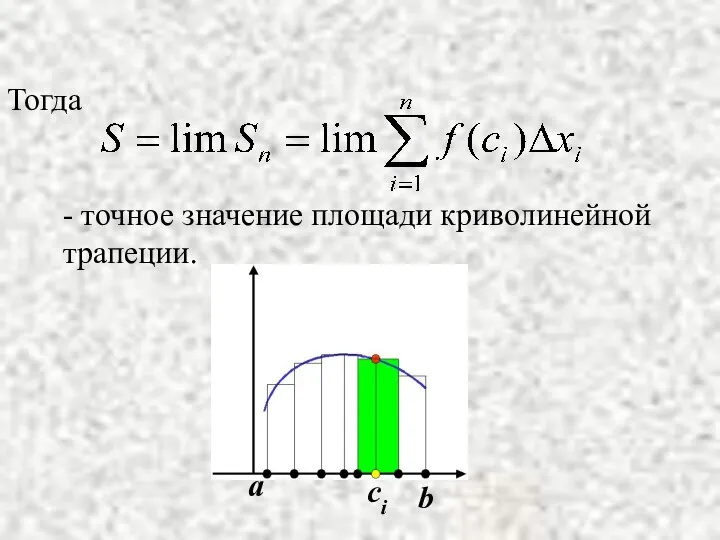
- 5. Тогда - точное значение площади криволинейной трапеции. a b ci
- 6. Определённый интеграл как предел интегральной суммы. Построенные выше суммы вида называются интегральными суммами для функции f(x)
- 7. зависит от способа разбиения [a,b] на части и от выбора точек на элементарном отрезке. a b
- 8. а - нижний предел, b - верхний предел интегрирования.
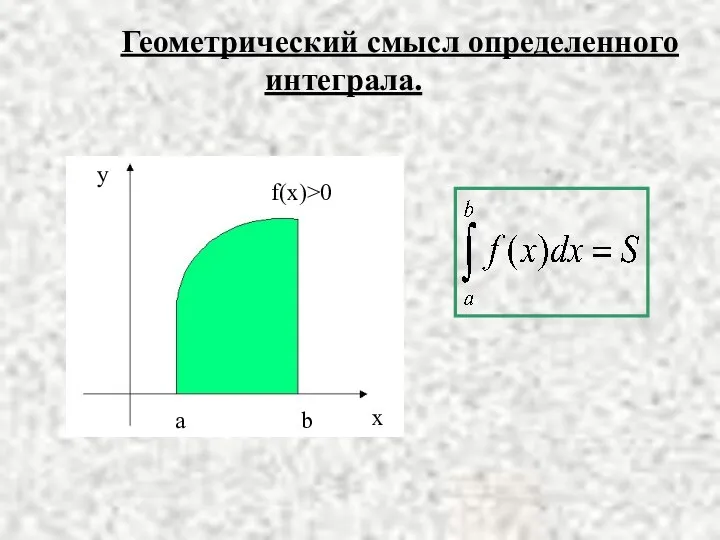
- 10. Геометрический смысл определенного интеграла.
- 11. Теорема существования : Если то
- 12. Замечания. 1. 2.
- 13. Свойства определенного интеграла. 1. Независимость величины интеграла от обозначения переменной интегрирования. 2. Линейность.
- 14. 3. Аддитивность (разбиение на сумму интегралов по частям отрезка). ( между а и в можно вставить
- 15. 4. Сохранение знака интеграла . Если то
- 16. 5. Интегрирование неравенств. Если то
- 17. 6. Теорема об оценке интеграла. Если то
- 18. 7. Теорема о среднем. Если то
- 19. Доказательство: Из теоремы об оценке
- 21. Скачать презентацию



![зависит от способа разбиения [a,b] на части и от выбора точек](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1459123/slide-6.jpg)



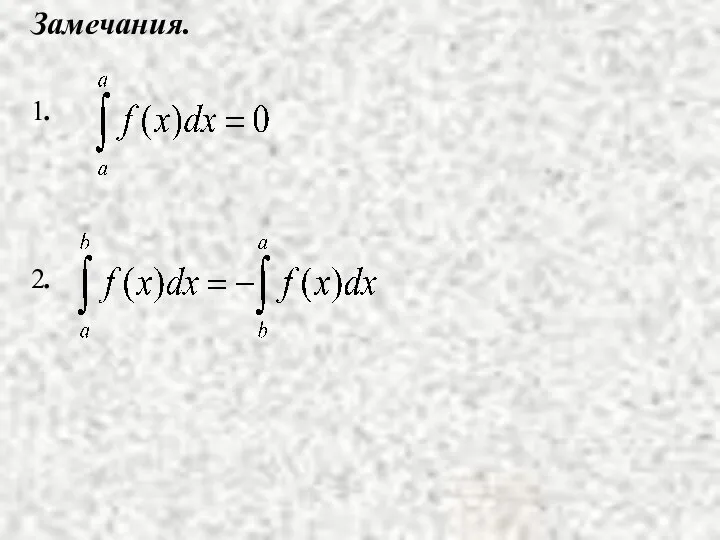







 Причина появления необходимости в дробях
Причина появления необходимости в дробях Решение текстовых задач. Задание В13, ЕГЭ
Решение текстовых задач. Задание В13, ЕГЭ Chapter 3. Polynomial and Rational Functions. 3.4 Zeros of Polynomial Functions
Chapter 3. Polynomial and Rational Functions. 3.4 Zeros of Polynomial Functions Обыкновенные дроби. Устная работа на уроках математики в 6 классе
Обыкновенные дроби. Устная работа на уроках математики в 6 классе Нахождение дроби от числа. 6 класс
Нахождение дроби от числа. 6 класс Решение логарифмических неравенств МКОУ «Средняя общеобразовательная школа № 6» городского округа город Фролово
Решение логарифмических неравенств МКОУ «Средняя общеобразовательная школа № 6» городского округа город Фролово Решение задач
Решение задач  Оптимизационные методы решения систем линейных алгебраических уравнений
Оптимизационные методы решения систем линейных алгебраических уравнений Множества и операции над ними. Решение задач с помощью кругов Эйлера
Множества и операции над ними. Решение задач с помощью кругов Эйлера Параллельные прямые. Задачи на готовых чертежах
Параллельные прямые. Задачи на готовых чертежах Cостав чисел 5-10 Математика 1 класс СРО Л.В. Занкова
Cостав чисел 5-10 Математика 1 класс СРО Л.В. Занкова  Теорема Фейербаха
Теорема Фейербаха Раскрытие скобок. Подготовила учитель математики МОУСОШ №2 п.Мокроус Фёдоровского района Саратовской области Дусбулатова
Раскрытие скобок. Подготовила учитель математики МОУСОШ №2 п.Мокроус Фёдоровского района Саратовской области Дусбулатова Matrix Equations and Systems of Linear Equations
Matrix Equations and Systems of Linear Equations Системы n линейных уравнений с m неизвестными. Теорема Кронекера-Капелли. Методы их решения. Тема 3
Системы n линейных уравнений с m неизвестными. Теорема Кронекера-Капелли. Методы их решения. Тема 3 Параллельные прямые. Геометрия 7 класс
Параллельные прямые. Геометрия 7 класс Область определения функции
Область определения функции Площадь треугольника
Площадь треугольника Решение неравенств и их систем
Решение неравенств и их систем Решение задания В8. Основные типы заданий
Решение задания В8. Основные типы заданий Многранники в нашей жизни
Многранники в нашей жизни Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Дроби. Происхождение дробей
Дроби. Происхождение дробей Муниципальное образовательное учреждение «Средняя общеобразовательная школа № 24»
Муниципальное образовательное учреждение «Средняя общеобразовательная школа № 24» Презентация на тему Раскрытие скобок
Презентация на тему Раскрытие скобок Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Измерение углов
Измерение углов Решение систем уравнений с двумя переменными
Решение систем уравнений с двумя переменными