- Главная
- Математика
- Ошибка измерения. Учет ошибки шкалы прибора и систематических ошибок. Оценка суммарной погрешности

Содержание
- 2. План Введение 1 Ошибка измерения 2. Измерительные шкалы 3. Классификация погрешности Заключение Литература
- 5. Измерительные шкалы Рассмотрим подробнее особенности различных измерительных шкал. С. Стивенсом предложена классификация из четырех типов шкал
- 6. ШКАЛА НАИМЕНОВАНИЙ(от лат. nomen – имя, название) используется для идентификации элементов множества. На этой шкале определены
- 7. ШКАЛА ПОРЯДКА, как и шкала наименований, является качественной, но позволяет не только именовать, но и ранжировать
- 8. Отличительной особенностью порядковой шкалы является то, что значения по этой шкале упорядочены. В рассмотренном примере минералы
- 9. ШКАЛА ИНТЕРВАЛОВ, в отличие от шкалы порядка, позволяет не только ранжировать элементы множества, но и задает
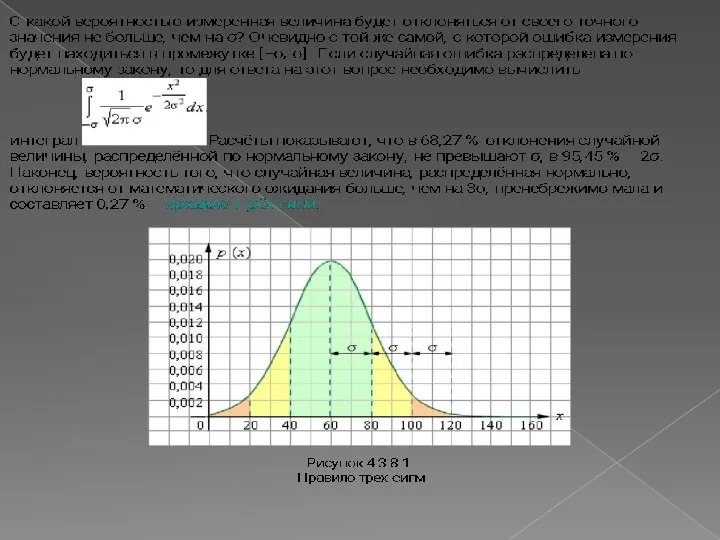
- 10. Принцип построения большинства интервальных шкал основан на правиле «трех сигм»: примерно 97,7—97,8 % всех значений признака
- 11. ШКАЛА ОТНОШЕНИЙ допускает линейные преобразования вида: y = a · x Шкала отношений, в отличие от
- 12. Классификация погрешностей Погрешности измерения классифицируются: 1) По способу выражения - абсолютные - относительные
- 13. Абсолютная погрешность
- 14. Приведенная погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному
- 15. 2) По источнику возникновения - инструментальные – составляющая погрешности, которая зависит от свойств СИТ (класс точности,
- 19. Алгоритм расчета: - Провести проверку на присутствие в выборке грубых ошибок - промахов. Обычно для этой
- 28. Погрешность измерения величин Пусть x – приближённое значение некоторой величины (например, полученное путём однократного измерения этой
- 36. Заключение
- 38. Скачать презентацию
План
Введение
1 Ошибка измерения
2. Измерительные шкалы
3. Классификация погрешности
Заключение
Литература
План
Введение
1 Ошибка измерения
2. Измерительные шкалы
3. Классификация погрешности
Заключение
Литература
Измерительные шкалы
Рассмотрим подробнее особенности различных измерительных шкал. С. Стивенсом предложена классификация
Измерительные шкалы
Рассмотрим подробнее особенности различных измерительных шкал. С. Стивенсом предложена классификация
1) номинативная (номинальная, шкала наименований);
2) порядковая (ординальная);
3) интервальная (шкала равных интервалов);
4) шкала равных отношений.
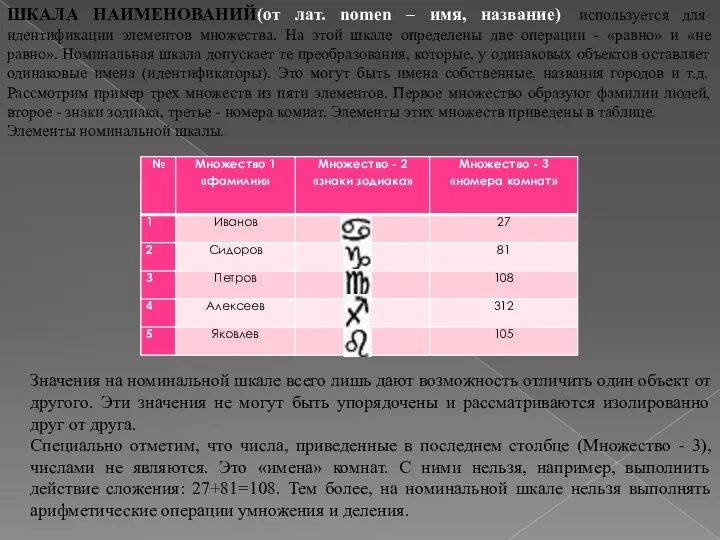
ШКАЛА НАИМЕНОВАНИЙ(от лат. nomen – имя, название) используется для идентификации элементов
ШКАЛА НАИМЕНОВАНИЙ(от лат. nomen – имя, название) используется для идентификации элементов
Элементы номинальной шкалы.
Значения на номинальной шкале всего лишь дают возможность отличить один объект от другого. Эти значения не могут быть упорядочены и рассматриваются изолированно друг от друга.
Специально отметим, что числа, приведенные в последнем столбце (Множество - 3), числами не являются. Это «имена» комнат. С ними нельзя, например, выполнить действие сложения: 27+81=108. Тем более, на номинальной шкале нельзя выполнять арифметические операции умножения и деления.
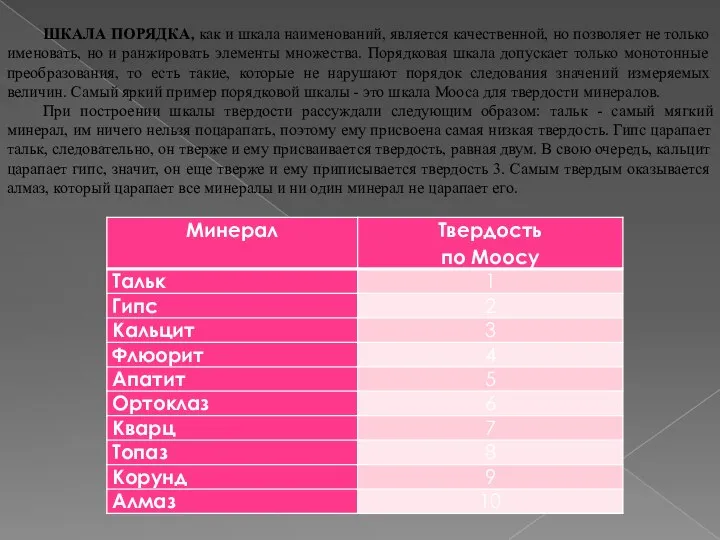
ШКАЛА ПОРЯДКА, как и шкала наименований, является качественной, но позволяет не только
ШКАЛА ПОРЯДКА, как и шкала наименований, является качественной, но позволяет не только
При построении шкалы твердости рассуждали следующим образом: тальк - самый мягкий минерал, им ничего нельзя поцарапать, поэтому ему присвоена самая низкая твердость. Гипс царапает тальк, следовательно, он тверже и ему присваивается твердость, равная двум. В свою очередь, кальцит царапает гипс, значит, он еще тверже и ему приписывается твердость 3. Самым твердым оказывается алмаз, который царапает все минералы и ни один минерал не царапает его.
Отличительной особенностью порядковой шкалы является то, что значения по этой шкале
Отличительной особенностью порядковой шкалы является то, что значения по этой шкале
Другой пример - это школьные отметки
Отметки имеют свои имена (1, 2, 3, 4, 5) и упорядочены. Нам известно, что 4 означает более высокий уровень знаний, чем 3, но не известно насколько. С отметками нельзя выполнять арифметические операции: 5-4=1, 3-2=1, 5-4=3-2 и т.д.. Ясно, что различие в знаниях между отличником и хорошистом не такое же, как между троечником и двоечником. Это общеизвестный факт. С другой стороны в образовательных учреждениях широко практикуется средний балл. Для определения среднего балла складывают, например, все отметки за год и делят на их количество. Это недопустимо. Ни складывать, ни делить отметки нельзя, так как они расположены на порядковой шкале*.
ШКАЛА ИНТЕРВАЛОВ, в отличие от шкалы порядка, позволяет не только ранжировать элементы
ШКАЛА ИНТЕРВАЛОВ, в отличие от шкалы порядка, позволяет не только ранжировать элементы
y = a · x + b
где а - положительное число, b - положительное или отрицательное число.
Изменение a приводит к изменению масштаба шкалы, изменение b вызывает сдвиг по шкале, то есть положение нуля на интервальной шкале не определено. Интервальные шкалы используются, например, для измерения температуры. При этом температурные интервалы равны, а положение нуля зависит от вида температурной шкалы, например по Цельсию, или по Фаренгейту. Если это неизвестно, то для описания закономерностей следует использовать отношение интервалов:
Принцип построения большинства интервальных шкал основан на правиле «трех сигм»: примерно
Принцип построения большинства интервальных шкал основан на правиле «трех сигм»: примерно
Американский психолог Р. Кеттелл предложил шкалу стенов – «стандартных десяток». Построение такой шкалы начинается с определения среднего арифметического значения в «сырых» баллах, которое принимается за точку отсчета. Вправо и влево отмеряются интервалы, равные 1/2 стандартного отклонения. Справа от среднего значения будут располагаться интервалы, равные 6, 7, 8, 9 и 10 стенам, слева – интервалы, равные 5, 4, 3, 2 и 1 стенам. На оси «сырых» баллов размечаются границы интервалов в единицах «сырых» баллов. Иногда в шкале стенов за разное количество «сырых» баллов будет начисляться одинаковое количество стенов. Шкалу стенов можно построить по любым данным, измеренным по крайней мере в порядковой шкале, при объеме выборки n > 200 и нормальном распределении признака.
ШКАЛА ОТНОШЕНИЙ допускает линейные преобразования вида:
y = a · x
Шкала отношений, в
ШКАЛА ОТНОШЕНИЙ допускает линейные преобразования вида:
y = a · x
Шкала отношений, в
Классификация погрешностей
Погрешности измерения классифицируются:
1) По способу выражения
- абсолютные
- относительные
Классификация погрешностей
Погрешности измерения классифицируются:
1) По способу выражения
- абсолютные
- относительные
Абсолютная погрешность
Абсолютная погрешность
Приведенная погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно
Приведенная погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно
,
где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
– если шкала прибора односторонняя, то есть нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
– если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
Приведенная погрешность является безразмерной величиной, либо измеряется в процентах).
2) По источнику возникновения
- инструментальные – составляющая погрешности, которая зависит от свойств СИТ (класс
2) По источнику возникновения
- инструментальные – составляющая погрешности, которая зависит от свойств СИТ (класс
- методические – составляющая общей погрешности измерения, которая обусловлена несовершенством метода измерения. Так, например, при измерении сопротивления на участке цепи при помощи омметра, величина измеренного сопротивления будет иметь методическую погрешность, за счет входного сопротивления самого омметра.
- личные, или субъективные - погрешность оператора
Алгоритм расчета:
- Провести проверку на присутствие в выборке грубых ошибок -
Алгоритм расчета:
- Провести проверку на присутствие в выборке грубых ошибок -
Пример:
В результате определения содержания алюминия в сплаве получены следующие значения (в % масс): 7.48, 7.49, 7.58, 7.47, 7.50. Нужно рассчитать среднее и доверительный интервал.
Решение:
Сначала проверяем на промах крайние значения. Наибольшее значение - 7.58. По Q-критерию: Q = (7.58 - 7.50) / (7.58 - 7.47) = 0.727. Оно больше табличного критического значения Qкритич(n = 5) = 0.64. Вывод - значение 7.58 является промахом, отбрасываем его. Убеждаемся, что остальные значения не являются промахами. Рассчитываем среднее: = (7.48 + 7.49 + 7.47 + 7.50) / 4 = 7.485 и дисперсию: V(x) = ((7.48 - 7.485)2 + (7.49 - 7.485)2 + (7.47 - 7.485)2 + (7.50- 7.485)2)/(4-1) = 0.000167. Число степеней свободы нашей дисперсии на единицу меньше числа значений: f = 4 - 1 = 3. Стандартное отклонение вычисляем, извлекая квадратный корень из дисперсии: S = 0.01291 Рассчитываем доверительный интервал, используя табличное значение критерия Стьюдента (t-критерия) t(f = 3, p = 0.95) = 3.18, = 3.18 * 0.01291 / 2 = 0.205269. Округляем доверительный интервал до одной значащей цифры: дельта= 0.2, и до этого же знака округляем среднее: среднее = 7.5
Ответ: 7.5 0.2
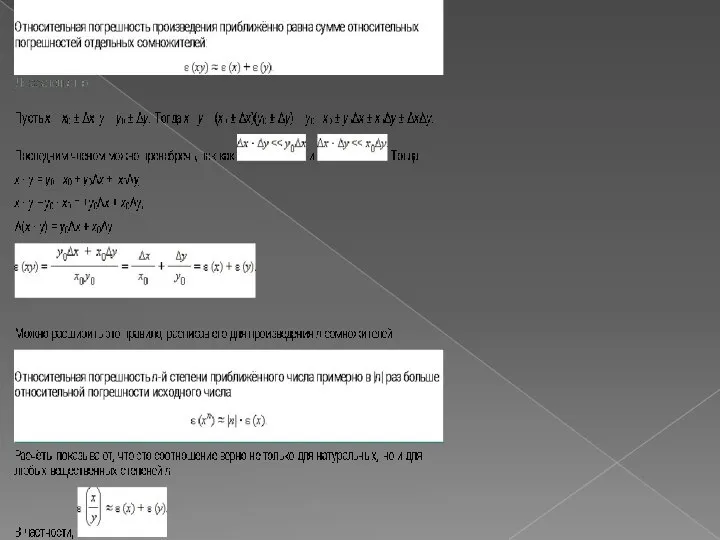
Погрешность измерения величин
Пусть x – приближённое значение некоторой величины (например, полученное путём однократного
Погрешность измерения величин
Пусть x – приближённое значение некоторой величины (например, полученное путём однократного
Заключение
Заключение





























 2 класс Математический диктант № 8 Выполнила Кирилова С.Г. Учитель начальных классов Школы «Ученики Пифагора» г. Лимассол, р.Кипр
2 класс Математический диктант № 8 Выполнила Кирилова С.Г. Учитель начальных классов Школы «Ученики Пифагора» г. Лимассол, р.Кипр Степень числа. 7 класс
Степень числа. 7 класс Презентация на тему Задачи на движение
Презентация на тему Задачи на движение  Модуль действительного числа
Модуль действительного числа Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Скалярное произведение векторов. Математический диктант
Скалярное произведение векторов. Математический диктант Презентация на тему Округление десятичных дробей
Презентация на тему Округление десятичных дробей  Елементи теорії виміру. Шкали виміру. Лекція 5. Тема 3
Елементи теорії виміру. Шкали виміру. Лекція 5. Тема 3 Решение задач по стереометрии
Решение задач по стереометрии Правила выполнения действий с натуральными числами
Правила выполнения действий с натуральными числами График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными ГИА - 2012. Открытый банк заданий по математике. (Задача 4)
ГИА - 2012. Открытый банк заданий по математике. (Задача 4) Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Делимость натуральных чисел
Делимость натуральных чисел Ромб. Свойства параллелограмма
Ромб. Свойства параллелограмма Планиметрия
Планиметрия Запись всех точек, соответствующих данным точкам единичной окружности
Запись всех точек, соответствующих данным точкам единичной окружности Сумма n-первых членов арифметической прогрессии
Сумма n-первых членов арифметической прогрессии Иррациональные уравнения и неравенства
Иррациональные уравнения и неравенства Формулы двойного аргумента
Формулы двойного аргумента Женщины в математике
Женщины в математике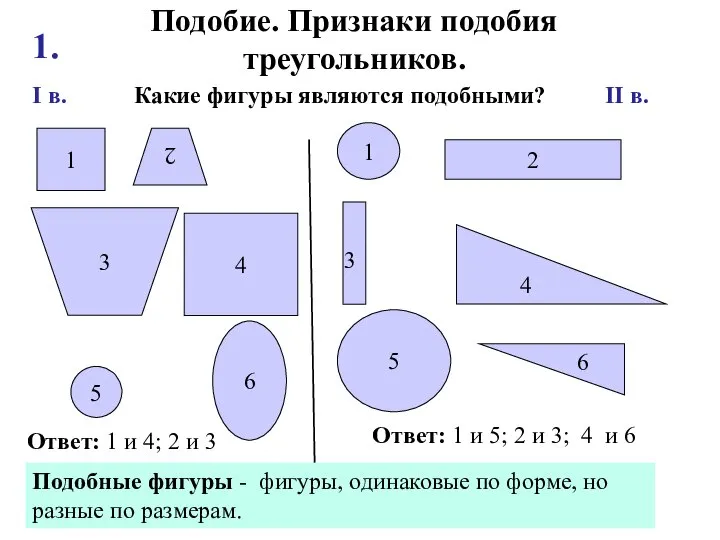 Подобие. Признаки подобия треугольников
Подобие. Признаки подобия треугольников Обыкновенные дроби
Обыкновенные дроби Презентация на тему Сумма углов треугольника
Презентация на тему Сумма углов треугольника  Муниципальное бюджетное образовательное учреждение «Лопхаринская средняя общеобразовательная школа» Урок математики в 5 кла
Муниципальное бюджетное образовательное учреждение «Лопхаринская средняя общеобразовательная школа» Урок математики в 5 кла Сумма углов треугольника
Сумма углов треугольника Кубик Рубика - гимнастика ума. Исследовательская работа
Кубик Рубика - гимнастика ума. Исследовательская работа Задачи оптимизации производства товаров и услуг
Задачи оптимизации производства товаров и услуг