Содержание
- 2. Указанные три вида зависимостей интенсивности отказов от времени можно получить, используя для вероятностного описания случайной наработки
- 3. Вероятность безотказной работы средняя наработки до отказа Отметим, что при параметре δ = 1 распределение Вейбулла
- 4. 2. Экспоненциальное распределение Как было отмечено выше экспоненциальное распределение вероятности безотказной работы является частным случаем распределения
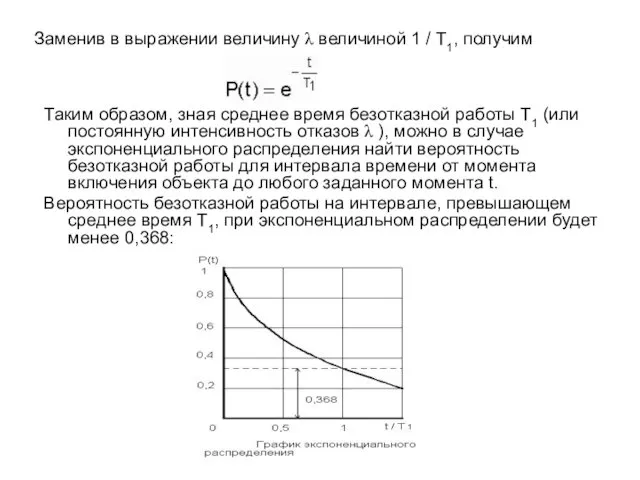
- 5. Заменив в выражении величину λ величиной 1 / Т1, получим Таким образом, зная среднее время безотказной
- 6. Длительность периода нормальной эксплуатации до наступления старения может оказаться существенно меньше Т1, то есть интервал времени
- 7. и для экспоненциального распределения соответственно равна: После некоторых преобразований получим: Таким образом, наиболее вероятные значения наработки,
- 8. 3. Распределение Рэлея Плотность вероятности в законе Рэлея имеет следующий вид где δ* - параметр распределения
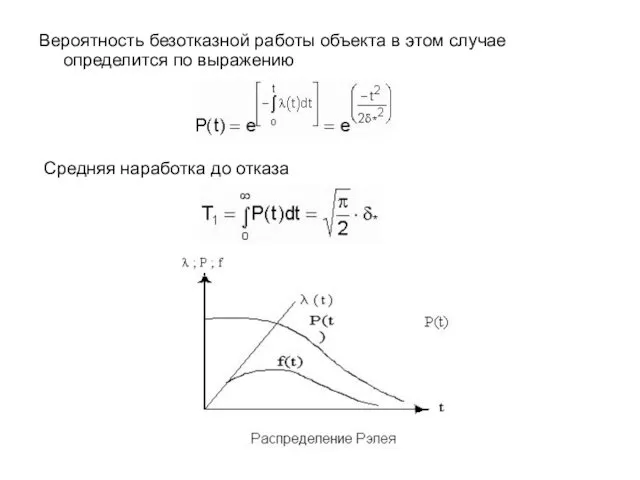
- 9. Вероятность безотказной работы объекта в этом случае определится по выражению Средняя наработка до отказа
- 10. 4. Нормальное распределение (распределение Гаусса) Нормальный закон распределения характеризуется плотностью вероятности вида где mx, σx -
- 11. На рисунке изображены кривые λ(t), Р(t) и f(t) для случая σt если неравенство σt
- 12. 5. Треугольное распределение Характеризует случайные величины, имеющие ограниченную область возможных значений (tн, tк). Положение и форму
- 13. Функция надежности Интенсивность отказа Медиана Математическое ожидание
- 15. 6. Гамма-распределение Гамма-распределение является двухпараметрическим распределением. Плотность распределения имеет ограничение с одной стороны (0 ≤ х
- 16. Математическое ожидание и дисперсия соответственно равны: Мx = α/λ; Dx = α/λ2 . При α 1
- 18. Скачать презентацию













 Четырехугольники 8 класс
Четырехугольники 8 класс Применение производной к исследованию функций
Применение производной к исследованию функций Методика работы с задачей на представление формульной зависимости в графическом виде
Методика работы с задачей на представление формульной зависимости в графическом виде Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Введение. Эконометрика и эконометрическое моделирование
Введение. Эконометрика и эконометрическое моделирование Правильные многогранники. Часть 1 - Платоновы тела
Правильные многогранники. Часть 1 - Платоновы тела Парабола
Парабола Шар, сфера, цилиндр
Шар, сфера, цилиндр Новый год в стране математики
Новый год в стране математики Решение дифференциальных уравнений. (Лекция 6)
Решение дифференциальных уравнений. (Лекция 6) Интеграл Лебега на прямой
Интеграл Лебега на прямой Преобразование графиков функции
Преобразование графиков функции Прямоугольный параллелепипед
Прямоугольный параллелепипед Эластичности и логарифмические модели
Эластичности и логарифмические модели Решение уравнений высших степеней с помощью замены переменной
Решение уравнений высших степеней с помощью замены переменной Умножение на 2
Умножение на 2 Математическое моделирование. Планы второго порядка
Математическое моделирование. Планы второго порядка Точки на прямой. Вопросы, упражнения
Точки на прямой. Вопросы, упражнения Учимся решать задачи 1 класс Шпаргалка для заботливых родителей
Учимся решать задачи 1 класс Шпаргалка для заботливых родителей  Вписанная окружность
Вписанная окружность КАК ЛЮДИ СЧИТАЛИ В СТАРИНУ И КАК ПИСАЛИ ЦИФРЫ Демонстрационный материал к уроку
КАК ЛЮДИ СЧИТАЛИ В СТАРИНУ И КАК ПИСАЛИ ЦИФРЫ Демонстрационный материал к уроку  Поворот. (Геометрія. 9 клас)
Поворот. (Геометрія. 9 клас) Презентация по математике "Система координат" - скачать
Презентация по математике "Система координат" - скачать  Метод следа
Метод следа Исследование качества школьного математического и естественнонаучного образования TIMSS
Исследование качества школьного математического и естественнонаучного образования TIMSS Решение логических задач методом рассуждений
Решение логических задач методом рассуждений Конус как тело вращения
Конус как тело вращения Descriptive statistics. Frequency distributions and their graphs. (Section 2.1)
Descriptive statistics. Frequency distributions and their graphs. (Section 2.1)