Содержание
- 2. ОСНОВНЫЕ ПОНЯТИЯ
- 3. ОСНОВНЫЕ ПОНЯТИЯ отказы ТС* ошибки операторов ТС внешние негативные воздействия *Отказ – это нарушение работоспособности** **Работоспособность
- 4. ОСНОВНЫЕ ПОНЯТИЯ отказ ТС; аварийный исход; образование поражающих факторов; поражение объектов воздействия; вторичные поражающие факторы; воздействия
- 5. ОСНОВНЫЕ СВЕДЕНИЯ Основная причина – отказ. Отказ – случайное события. Параметры, описывающие случайные события, – случайные
- 6. В основе обработки случайных величин лежат знания вероятностных закономерностей случайных событий, являющихся предметом теории вероятностей. ОСНОВНЫЕ
- 7. Данные знания позволяют построить закономерности изменения численных характеристик, описывающих случайные события. Методы теории вероятностей широко применяются
- 8. Достоверное событие – событие, которое произойдет при соблюдении определенных условий. Например, отказ. Невозможное событие – событие,
- 9. Не совместные (совместные) события – события, появление одного из которых исключает (не исключает) возможности появления другого.
- 10. Генеральная совокупность N – полный набор всех возможных значений, которые может принимать случайная физическая величина. Выборка
- 11. Цель обработки набора значений величин xi выборки – определение закономерностей, описывающих генеральную совокупность. ОСНОВНЫЕ СВЕДЕНИЯ
- 12. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Абсолютная частота случайного события А – количество m проявления данного события, зафиксированного в объеме
- 13. При малом количестве испытаний в серии значения W для разных серий различны – Wk где Р
- 14. Из определения вероятности вытекают свойства: вероятность случайного события есть положительное число 0 ≤ Р(A) ≤ 1
- 15. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Теорема сложения вероятностей Сумма вероятностей двух несовместных противоположных событий, образующих полную группу Если события
- 16. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Теорема умножения вероятностей независимые события: Условная вероятность события А Р(A/B) – вероятность события А,
- 17. Функция распределения Многократные равноточные измерения физической величины – выборка xi. Истинное значение х0 измеряемой величины Х
- 18. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Для каждого интервала получим значения: абсолютной частоты – m1 , m2 , …, mk;
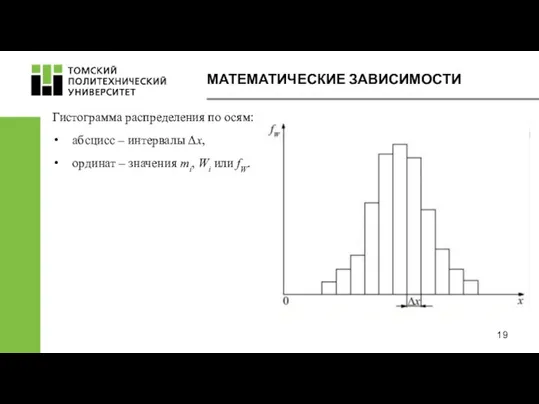
- 19. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Гистограмма распределения по осям: абсцисс – интервалы Δx, ординат – значения mi, Wi или
- 20. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Для каждого числа х в диапазоне изменения случайной величины Х существует определенная вероятность Р(Х
- 21. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Плотность вероятности Плотность вероятности – производная от функции распределения: Находится при условии: число интервалов
- 22. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Плотность вероятности (площадь под кривой в интервале х∈[xi, xi+dx]) позволяет вычислить вероятность попадания случайной
- 23. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Во многих случаях нет необходимости пользоваться функциями F(t) или f(t), достаточно знать числовые характеристики
- 24. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Числовые характеристики В теории надежности наиболее распространены: среднеарифметическое значение; математическое ожидание; дисперсия; среднеквадратичное отклонение.
- 25. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Математическое ожидание – наиболее вероятное значение случайной величины: для дискретных случайных величин для непрерывных
- 26. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Дисперсия – мера отклонения случайной величины Х от ее математического ожидания М(х): для дискретных
- 27. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ На практике M(x) и D(x) случайной величины можно оценить только на основе выборки из
- 28. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ
- 29. Законы распределения случайных величин Закон распределения случайной величины – функциональная зависимость между возможными значениями случайной величины
- 30. Наибольшее распространение получили законы: для дискретных случайных величин: биноминальный закон; закон Пуассона; для непрерывных случайных величин:
- 31. Закон Пуассона Описывает закономерность появления случайных отказов в сложных системах. Случайная величина Х распределена по закону
- 32. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Параметр распределения λ=np, где n – общее количество испытаний; p – вероятность появления ожидаемого
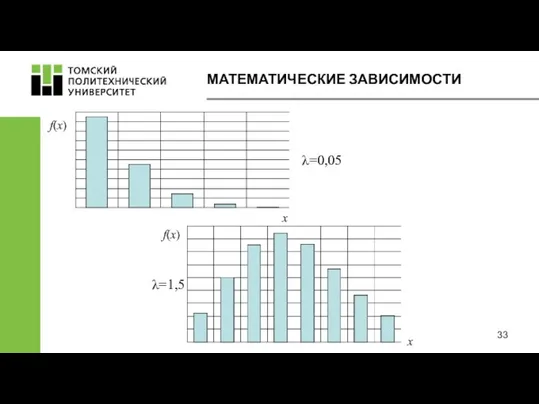
- 33. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ f(x) λ=0,05 λ=1,5 f(x) x x
- 34. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Экспоненциальный закон Основной закон, т.к. описывает закономерность появления отказов в период нормальной эксплуатации изделий:
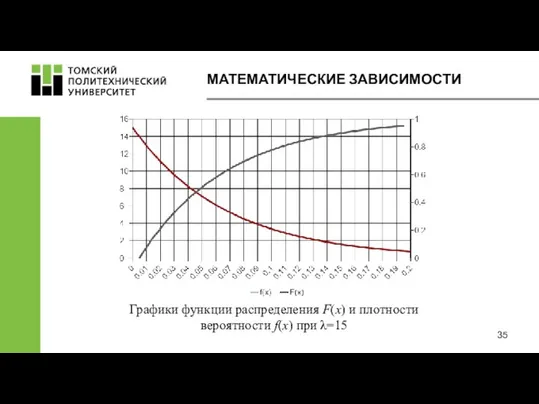
- 35. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Графики функции распределения F(x) и плотности вероятности f(x) при λ=15
- 36. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Нормальный закон Используют для описания постепенных отказов, когда распределение времени безотказной работы вначале имеет
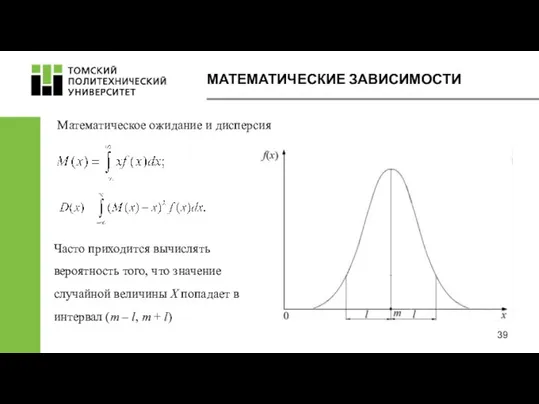
- 37. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Плотность вероятности и функция распределения: где m – математическое ожидание, мода, медиана; σ –
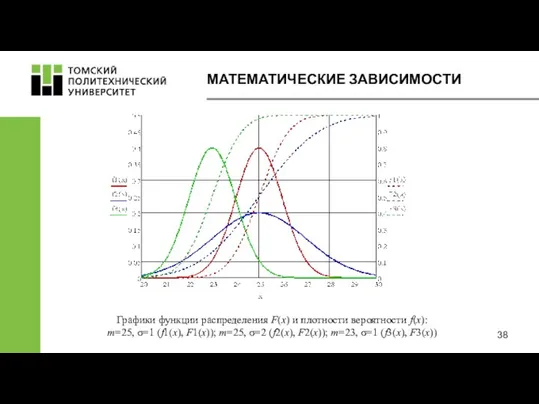
- 38. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Графики функции распределения F(x) и плотности вероятности f(x): m=25, σ=1 (f1(x), F1(x)); m=25, σ=2
- 39. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Математическое ожидание и дисперсия Часто приходится вычислять вероятность того, что значение случайной величины X
- 40. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Вероятность, с которой в условиях данного эксперимента полученные экспериментальные данные можно считать надежными либо
- 41. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Вероятность попадания значения случайной величины Х в интервал (m – l, m + l),
- 42. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Закон Вейбулла-Гнеденко Универсальный – при соответствующих значениях переходит в нормальное, экспоненциальное и другие. Закон
- 43. МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Функция распределения α – параметр формы (определяется подбором в результате обработки экспериментальных данных); λ
- 45. Скачать презентацию



















![МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ Плотность вероятности (площадь под кривой в интервале х∈[xi, xi+dx])](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1449068/slide-21.jpg)

















 Стрельцова Марина Вячеславовна Учитель математики МОУ «СОШ 12» Города Щекино
Стрельцова Марина Вячеславовна Учитель математики МОУ «СОШ 12» Города Щекино  Дробные выражения
Дробные выражения Алгоритм решения и успех на ЕГЭ
Алгоритм решения и успех на ЕГЭ Доказательство числовых неравенств
Доказательство числовых неравенств Мой любимый предмет – геометрия. «Геометрия – прообраз красоты мира.» И. Кеплер. 11 класс
Мой любимый предмет – геометрия. «Геометрия – прообраз красоты мира.» И. Кеплер. 11 класс Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Линейка. 2 класс
Линейка. 2 класс Готовимся к ЕГЭ. Стереометрия
Готовимся к ЕГЭ. Стереометрия Станцо В.В., Савин А.П. Занимательная математика в рассказах для детей
Станцо В.В., Савин А.П. Занимательная математика в рассказах для детей Многогранники
Многогранники Графы и деревья. Кроссворд
Графы и деревья. Кроссворд Презентация для класса Проверяем, верно ли» 1 класс
Презентация для класса Проверяем, верно ли» 1 класс  Разбор задач
Разбор задач Առարկա՝ «Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում» (ընտրովի դասընթաց)
Առարկա՝ «Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում» (ընտրովի դասընթաց) Непрерывность функции в точке и на отрезке
Непрерывность функции в точке и на отрезке Координаты на плоскости. 6 класс
Координаты на плоскости. 6 класс Формулы сокращенного умножения
Формулы сокращенного умножения Готовимся к Всероссийским проверочным работам по математике
Готовимся к Всероссийским проверочным работам по математике Тіктөртбұрыш пен шаршының ауданы
Тіктөртбұрыш пен шаршының ауданы Умножение и деление на однозначное число
Умножение и деление на однозначное число Подобие треугольников
Подобие треугольников Правильные и неправильные дроби. 5 класс
Правильные и неправильные дроби. 5 класс Симплекс-метод
Симплекс-метод Геометрический тренинг
Геометрический тренинг Сума кутів трикутника
Сума кутів трикутника Пропорции в нашем мире
Пропорции в нашем мире Аттестационная работа. Программа дополнительного образования Одаренные дети
Аттестационная работа. Программа дополнительного образования Одаренные дети Презентация по математике "Математика и природа" - скачать
Презентация по математике "Математика и природа" - скачать