Содержание
- 2. * Лекция 7 Основные теоремы и зависимости математической статистики 11-05 Какие задачи стоят перед математической статистикой?
- 3. * Лекция 7 Основные теоремы и зависимости математической статистики 11-10 Одними из основных понятий математической статистики
- 4. * Лекция 7 Основные теоремы и зависимости математической статистики 11-20 Опр.1. Испытание (опыт) – это действие,
- 5. * Лекция 7 Основные теоремы и зависимости математической статистики 11-25 Действия над событиями 1) Сумма событий:
- 6. * Лекция 7 Основные теоремы и зависимости математической статистики 11-30 Пример: Два стрелка производят по одному
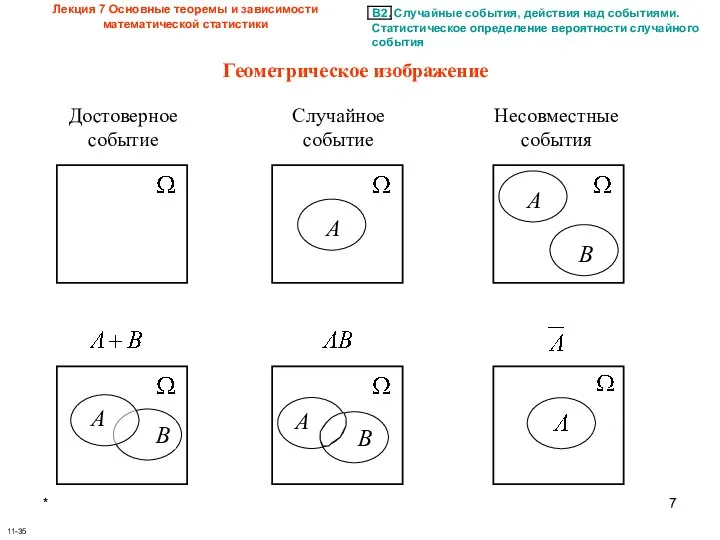
- 7. * Лекция 7 Основные теоремы и зависимости математической статистики 11-35 Геометрическое изображение Достоверное событие Случайное событие
- 8. * Лекция 7 Основные теоремы и зависимости математической статистики 11-40 2.2. Статистическое определение вероятности Опр.1. Пусть
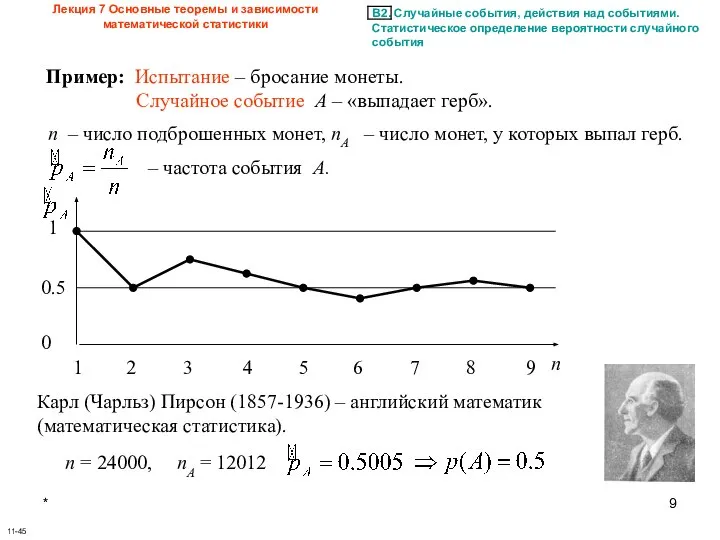
- 9. * Лекция 7 Основные теоремы и зависимости математической статистики 11-45 Пример: Испытание – бросание монеты. Случайное
- 10. * Лекция 7 Основные теоремы и зависимости математической статистики 11-50 Классическое определение вероятности Опр.3. Пусть n
- 11. * Лекция 7 Основные теоремы и зависимости математической статистики 11-55 Опр. События A и B называются
- 12. * Лекция 7 Основные теоремы и зависимости математической статистики 12-00 Пример: Производится стрельба по цели из
- 13. * Лекция 7 Основные теоремы и зависимости математической статистики 12-05 Т.4. Вероятность суммы двух произвольных (совместных
- 14. * Лекция 7 Основные теоремы и зависимости математической статистики 12-10 Т.5. Вероятность суммы любого числа произвольных
- 15. В4. Случайные величины дискретного типа, их закон распределения, числовые характеристики случайных величин Опр. 1. Случайная величина
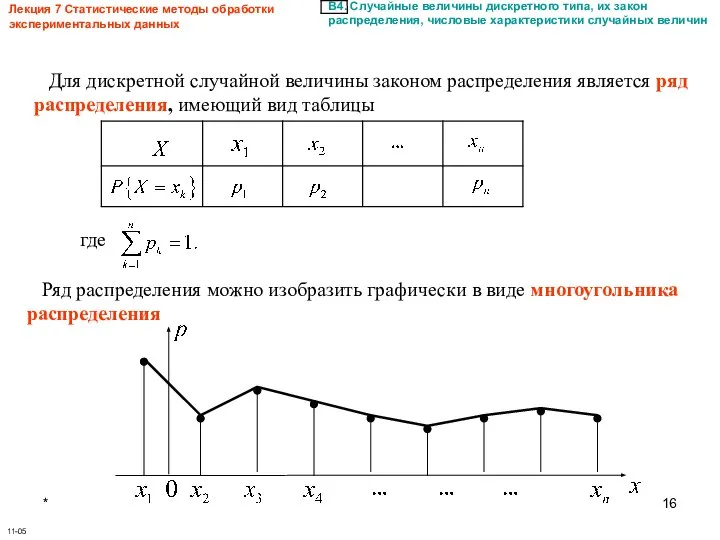
- 16. * Лекция 7 Статистические методы обработки экспериментальных данных 11-05 Для дискретной случайной величины законом распределения является
- 17. * Лекция 7 Статистические методы обработки экспериментальных данных 11-05 Пример 1: Производится три выстрела по цели.
- 19. Скачать презентацию













 Решение квадратных неравенств
Решение квадратных неравенств Графи. Основні поняття і визначення
Графи. Основні поняття і визначення Кривые 2-го порядка: эллипс, гипербола, парабола
Кривые 2-го порядка: эллипс, гипербола, парабола Характеристическое свойство арифметической прогрессии
Характеристическое свойство арифметической прогрессии Муниципальное общеобразовательное учреждение гимназия № 3 Муниципальное общеобразовательное учреждение гимназия № 3 Электи
Муниципальное общеобразовательное учреждение гимназия № 3 Муниципальное общеобразовательное учреждение гимназия № 3 Электи Построение графика квадратичной функции. (8 класс)
Построение графика квадратичной функции. (8 класс) Игра Назови соседа. 1 класс. Математика
Игра Назови соседа. 1 класс. Математика Презентация по математике "«Деление» 4 класс" - скачать бесплатно
Презентация по математике "«Деление» 4 класс" - скачать бесплатно Аналитические функции
Аналитические функции Неопределённый интеграл, его свойства . Непосредственное интегрирование. Метод замены переменной в неопределенном интеграле
Неопределённый интеграл, его свойства . Непосредственное интегрирование. Метод замены переменной в неопределенном интеграле Нумерация многозначных чисел (4 класс)
Нумерация многозначных чисел (4 класс) Пересекающиеся прямые. Вертикальные и смежные углы
Пересекающиеся прямые. Вертикальные и смежные углы Презентация по математике "Число и цифра 8" - скачать
Презентация по математике "Число и цифра 8" - скачать  Показательные уравнения
Показательные уравнения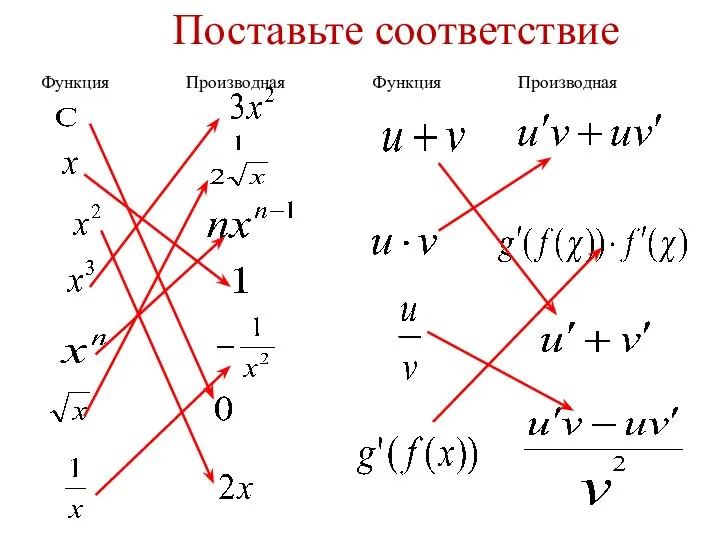 Функция Производная
Функция Производная Многогранники
Многогранники Математическое моделирование
Математическое моделирование Ах, уж эти дроби! Урок математики 6 класс Учитель: Тиунова Е.П.
Ах, уж эти дроби! Урок математики 6 класс Учитель: Тиунова Е.П.  Исследование функций и построение графиков
Исследование функций и построение графиков Средние величины. Понятие средней величины
Средние величины. Понятие средней величины Признак Даламбера. Радикальный признак Коши. Интегральный признак Коши. (Семинар 26)
Признак Даламбера. Радикальный признак Коши. Интегральный признак Коши. (Семинар 26) Расстояние от точки до прямой. Перпендикулярные прямые
Расстояние от точки до прямой. Перпендикулярные прямые Окружность и круг
Окружность и круг Презентация по математике "Сравнение рациональных чисел" - скачать
Презентация по математике "Сравнение рациональных чисел" - скачать  Головоломки на разрезание
Головоломки на разрезание Векторы. Действия над векторами. Проекция вектора
Векторы. Действия над векторами. Проекция вектора Преобразования координат на плоскости
Преобразования координат на плоскости Числовые промежутки
Числовые промежутки