Содержание
- 2. Домашнее задание (проверка) 16. Для вариационного ряда Найдем математическое ожидание, дисперсию, вариацию:
- 3. Точечные оценки параметров Пусть случайная величина Х имеет закон распределения, зависящий от параметра θ (тэта): F(x,θ).
- 4. Точечные оценки параметров Оценки называются точечными, так как они оценивают одно численное значение параметра (точку). Пусть
- 5. Точечные оценки параметров выборочная доля является несмещенной, состоятельной и эффективной оценкой генеральной доли р: Для указанных
- 6. Пример 1: Из 1500 деталей отобрано 250, распределение которых по размеру Х задано в таблице: Найти
- 7. Пример 1 (продолжение): Вычислим дисперсию оценки среднего: для повторной выборки: для бесповторной выборки
- 8. Пример 2: Выборочно обследовали партию кирпича. Из 100 проб в 12 случаях кирпич оказался бракованным. Найти
- 9. Метод наименьших квадратов для нахождения точечных оценок: Исследуется зависимость двух случайных величин Y и Х по
- 10. Пример 3: Найти оценки параметров a и b по результатам выборочного наблюдения, если связь между случайными
- 11. Пример 3 (продолжение): Разделим оба равенства на n и обозначим выборочные средние: Тогда получим систему линейных
- 12. Интервальные оценки параметров Интервальная оценка параметра дает возможность определить точность и надежность его оценки. Интервальной оценкой
- 13. Интервальные оценки параметров Обычно доверительный интервал симметричен относительно точечной оценки , т.е. имеет вид , где
- 14. 1. Доверительный интервал для генеральной средней а а) для повторной выборки б) для бесповторной выборки Величина
- 15. Пример 4: Для определения среднего процентного содержания белка в зернах пшеницы было отобрано 625 зерен, обследование
- 16. Пример 5: Выборочное среднее квадратическое отклонение десяти измерений некоторой величины равно 10 см. Найти с надежностью
- 17. Пример 6: Из партии в 5000 электрических ламп было отобрано 300 по схеме бесповторной выборки. Средняя
- 18. 2. Доверительный интервал для генеральной доли признака р: а) для повторной выборки б) для бесповторной выборки
- 19. Пример 7: В партии, содержащей 5000 изделий, проверено 400. Среди них оказалось 300 изделий высшего сорта.
- 20. Пример 8: Среди стандартных изделий одной фабрики в среднем 15% относится ко второму сорту. С какой
- 21. 3. Доверительный интервал для генеральной дисперсии Где и определяются из условия Обычно они определяются так, чтобы
- 22. Пример 9: Признак Х генеральной совокупности распределен нормально. Имеется выборка в виде таблицы Найти доверительный интервал,
- 23. Пример 9 (продолжение): По условию задачи n=20, γ=0,99. Доверительный интервал для генеральной дисперсии равен: Где и
- 24. 4. Объем выборки n, необходимый для достижения требуемой надежности γ При параметре а повторная выборка –
- 25. Пример 10: Найти объемы повторной и бесповторной выборок из 10000 банок консервов для определения доли банок,
- 26. Пример 10 (продолжение): Для бесповторной выборки объем равен В этом случае наибольшее значение выражения w(1-w) соответствует
- 27. Тестовые вопросы 1. Характеристикой оценок числовых характеристик по результатам выборочных значений является: а) репрезентативность оценки; б)
- 28. Тестовые вопросы 3. Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может
- 29. Тестовые вопросы 5. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие
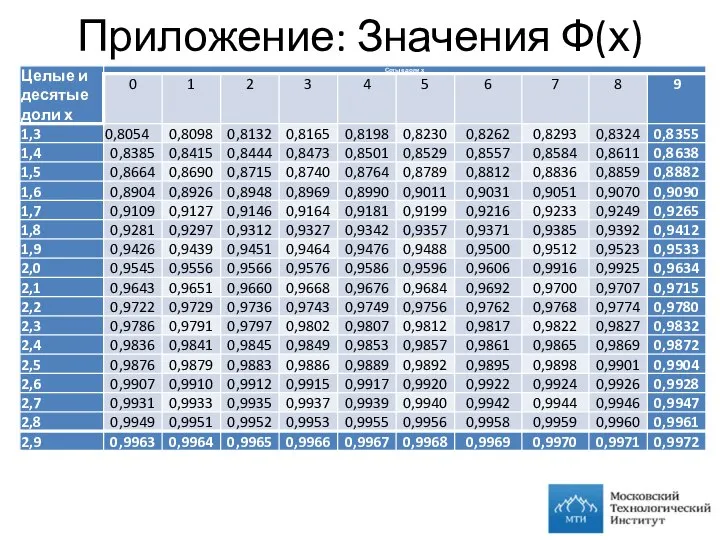
- 30. Приложение: Значения Ф(х)
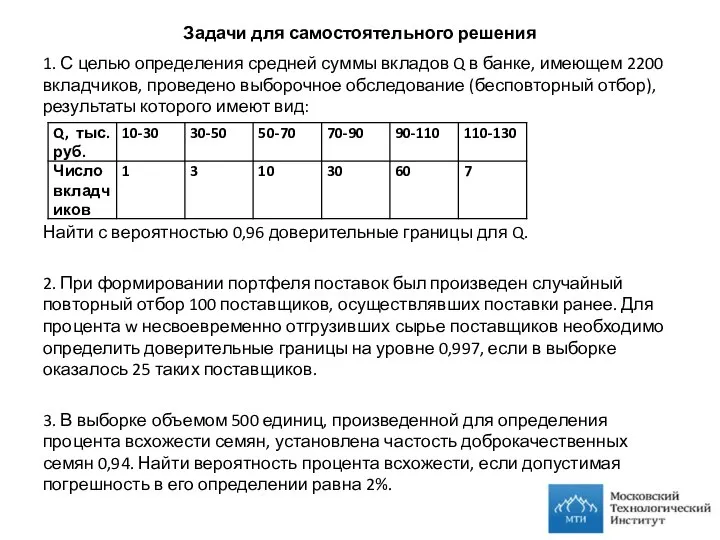
- 31. Задачи для самостоятельного решения 1. С целью определения средней суммы вкладов Q в банке, имеющем 2200
- 33. Скачать презентацию




























 Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Умножение и его свойства. 5 класс
Умножение и его свойства. 5 класс Геометрические характеристики сечений
Геометрические характеристики сечений Пифагор - человек-легенда. Исследовательская работа
Пифагор - человек-легенда. Исследовательская работа Математические основы психологии
Математические основы психологии Отрезок. Прямая. Луч
Отрезок. Прямая. Луч Аксиомы стереометрии. Следствия из аксиом
Аксиомы стереометрии. Следствия из аксиом Логарифмические неравенства
Логарифмические неравенства Устная работа. Логарифмы. 10 класс
Устная работа. Логарифмы. 10 класс Практическое применение интегралов в различных областях
Практическое применение интегралов в различных областях Алгоритм исследования функции одного аргумента
Алгоритм исследования функции одного аргумента Метод выборочного наблюдения социально-экономических явлений и процессов
Метод выборочного наблюдения социально-экономических явлений и процессов Теорема о соотношениях между сторонами и углами треугольника
Теорема о соотношениях между сторонами и углами треугольника Презентация по математике "Математики и их открытия в годы Великой Отечественной войны" - скачать
Презентация по математике "Математики и их открытия в годы Великой Отечественной войны" - скачать  Теорема про три перпендикуляри
Теорема про три перпендикуляри Координаты вектора
Координаты вектора График и свойства степенной функции
График и свойства степенной функции деление обыкновенных дробей
деление обыкновенных дробей Решение треугольников
Решение треугольников Линейные уравнения с параметрами (7 класс)
Линейные уравнения с параметрами (7 класс) Урок-презентация в 3 классе учитель: Люлякина И.Ю. МБОУ «СОШ №12» г.Астрахань.
Урок-презентация в 3 классе учитель: Люлякина И.Ю. МБОУ «СОШ №12» г.Астрахань. Решение задач на движение по окружности
Решение задач на движение по окружности Квадратичная функция , её график и свойства
Квадратичная функция , её график и свойства Дроби и деление натуральных чисел
Дроби и деление натуральных чисел Задачи по теме «Призма и пирамида»
Задачи по теме «Призма и пирамида» Задания по математике (5 класс, часть 2)
Задания по математике (5 класс, часть 2) Перебор возможных вариантов
Перебор возможных вариантов История развития математики
История развития математики