- Главная
- Математика
- Парадокс маляра

Содержание
Слайд 2
Парадокс маляра́ — математический парадокс , утверждающий, что фигуру с бесконечной
Парадокс маляра́ — математический парадокс , утверждающий, что фигуру с бесконечной
площадью поверхности можно окрасить конечным количеством краски .
Слайд 3
Утверждение «для того, чтобы покрасить фигуру бесконечной площади, необходимо бесконечное количество
Утверждение «для того, чтобы покрасить фигуру бесконечной площади, необходимо бесконечное количество
краски» исходит из того, что фигура покрывается слоем краски одинаковой толщины.
Предлагаемый же способ окраски предполагает, что каждый следующий сегмент будет покрыт всё более тонким слоем, так что бесконечная сумма объёмов краски, ушедших на каждый сегмент площадью в 1π см2, будет сходиться к конечному значению.
При этом нужно иметь в виду, что предложенное математическое решение не учитывает тот физический факт, что слой краски не может иметь толщину меньше размера одной молекулы краски. Так как построенный описанным способом сосуд будет книзу сужаться до бесконечно малых диаметров, то при «заливке» краски в такой сосуд эта краска просто не «затечёт» в те его области, диаметр которых меньше диаметра молекулы краски. И тем не менее, с точки зрения математической модели, не учитывающей физические аспекты устройства нашего мира, описанное решение является верным, несмотря на парадоксальность.
Возможно, может показаться абсурдным, что сосуд бесконечной длины может иметь конечный объём (в данном случае 2π), да при этом ещё и вмещать в себя пластинку, площадь которой бесконечна. Но дело в том, что длина, площадь и объём — это разные величины. В математических моделях вполне возможны фигуры, имеющие бесконечную площадь при конечном объёме (или бесконечную длину при конечной площади).
Предлагаемый же способ окраски предполагает, что каждый следующий сегмент будет покрыт всё более тонким слоем, так что бесконечная сумма объёмов краски, ушедших на каждый сегмент площадью в 1π см2, будет сходиться к конечному значению.
При этом нужно иметь в виду, что предложенное математическое решение не учитывает тот физический факт, что слой краски не может иметь толщину меньше размера одной молекулы краски. Так как построенный описанным способом сосуд будет книзу сужаться до бесконечно малых диаметров, то при «заливке» краски в такой сосуд эта краска просто не «затечёт» в те его области, диаметр которых меньше диаметра молекулы краски. И тем не менее, с точки зрения математической модели, не учитывающей физические аспекты устройства нашего мира, описанное решение является верным, несмотря на парадоксальность.
Возможно, может показаться абсурдным, что сосуд бесконечной длины может иметь конечный объём (в данном случае 2π), да при этом ещё и вмещать в себя пластинку, площадь которой бесконечна. Но дело в том, что длина, площадь и объём — это разные величины. В математических моделях вполне возможны фигуры, имеющие бесконечную площадь при конечном объёме (или бесконечную длину при конечной площади).


 Отношение эквивалентности и фактор-множество
Отношение эквивалентности и фактор-множество Что узнали. Чему научились (урок № 80)
Что узнали. Чему научились (урок № 80) Модуль действительного числа. (8 класс)
Модуль действительного числа. (8 класс) Открытый урок по математике в 6 классе по теме: «Арифметические действия с дробями» Учитель математики: Варенко Оксана Валентино
Открытый урок по математике в 6 классе по теме: «Арифметические действия с дробями» Учитель математики: Варенко Оксана Валентино Муниципальное общеобразовательное учреждение средняя общеобразовательная школа № 2 городского поселения «Рабочий посёлок В
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа № 2 городского поселения «Рабочий посёлок В Математические диктанты. Часть 1. Повторение по курсу 7 класса
Математические диктанты. Часть 1. Повторение по курсу 7 класса Примеры решения тригонометрических уравнений
Примеры решения тригонометрических уравнений Уведення поняття "кілограм"
Уведення поняття "кілограм" Производные высших порядков
Производные высших порядков Введение в математическую логику и теорию алгоритмов
Введение в математическую логику и теорию алгоритмов Модель линейной парной регрессии
Модель линейной парной регрессии Уравнения, сводящиеся к квадратным
Уравнения, сводящиеся к квадратным Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Скрещивающиеся прямые
Скрещивающиеся прямые Соотношения между тригонометрическими функциями одного и того же угла
Соотношения между тригонометрическими функциями одного и того же угла Вероятность события. Первый и второй вид задач
Вероятность события. Первый и второй вид задач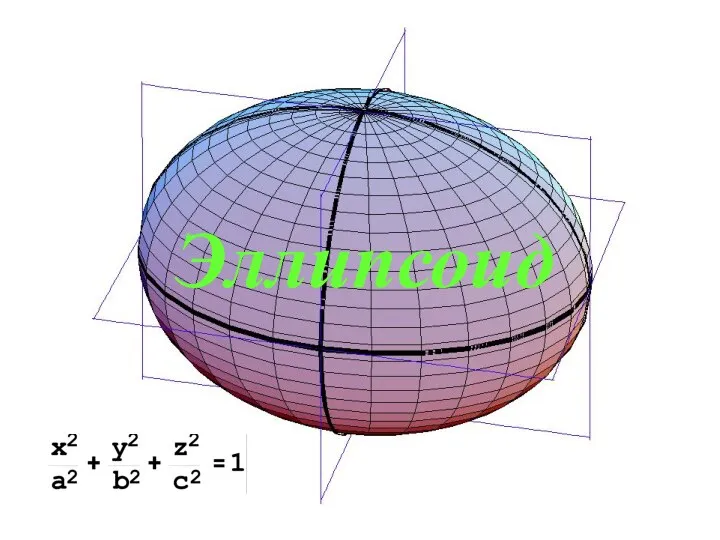 Эллипсоид. Все сечения
Эллипсоид. Все сечения Элементы многоугольника
Элементы многоугольника Matlab Linear Programming
Matlab Linear Programming Производная сложной функции
Производная сложной функции Математическая рыбалка. Интерактивная мозаика
Математическая рыбалка. Интерактивная мозаика Повторение и систематизация учебного материала. Логорифмы
Повторение и систематизация учебного материала. Логорифмы Занимательные головоломки
Занимательные головоломки Сложение и Вычитание в столбик 2 Класс - Презентация по математике_
Сложение и Вычитание в столбик 2 Класс - Презентация по математике_ Теория вероятностей
Теория вероятностей Занятие по формированию элементарных математических представлений. Тема Насекомые
Занятие по формированию элементарных математических представлений. Тема Насекомые Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении)
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) Презентация на тему Законы арифметических действий.
Презентация на тему Законы арифметических действий.