Содержание
- 2. Параллельный перенос Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (х; у; z)
- 3. Свойства параллельного переноса Сформулируем некоторые свойства параллельного переноса: 1.Параллельные перенос есть движение. 2.При параллельном переносе точки
- 4. Параллельный перенос является движением Докажем, что параллельный перенос является движением. При параллельном переносе на вектор и
- 5. Рассмотрим вектор Рис. 1. Рис. 2. По правилу треугольника (Рис. 12) или (Рис. 13)
- 6. Так как , значит . Мы доказали, что при параллельном переносе расстояние между точками сохраняется, значит,
- 7. Преобразования подобия
- 8. Преобразование фигуры F в фигуру F' называется преобразованием подобия, если при этом преобразовании расстояния между точками
- 9. Гомотетия - есть преобразования подобия. Доказательство. Пусть О — центр гомотетии, k — коэффициент гомотетии, X
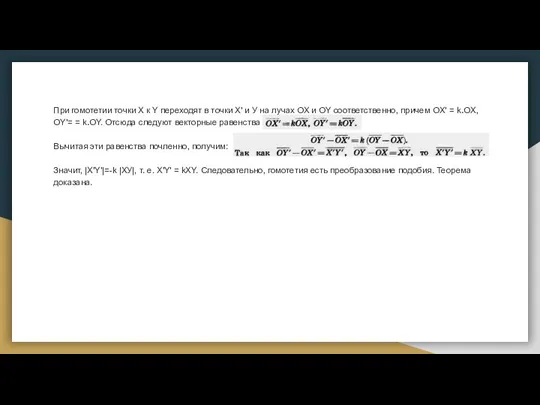
- 10. При гомотетии точки X к Y переходят в точки X' и У на лучах ОХ и
- 12. Скачать презентацию








 Стереометрия. Построение сечений многогранников
Стереометрия. Построение сечений многогранников Единичная окружность. Тренажер
Единичная окружность. Тренажер Первый урок алгебры в 7 классе
Первый урок алгебры в 7 классе Лемма. Параллельность трёх прямых
Лемма. Параллельность трёх прямых Решение задач
Решение задач Элементы теории вероятностей
Элементы теории вероятностей «Лунтик учится считать». Тренажёр по математике для 1 класса
«Лунтик учится считать». Тренажёр по математике для 1 класса Асимптоты функции
Асимптоты функции В страну математики. Задания
В страну математики. Задания Пропорция. Основное свойство пропорции. Решение пропорций
Пропорция. Основное свойство пропорции. Решение пропорций Презентация по математике "из Простоквашино. Задачи на дроби и проценты." - скачать
Презентация по математике "из Простоквашино. Задачи на дроби и проценты." - скачать  Аттестационная работа. Организация исследовательской деятельности учащихся по математике
Аттестационная работа. Организация исследовательской деятельности учащихся по математике Статистические методы анализа связей
Статистические методы анализа связей Планіметрія
Планіметрія Понятие функции
Понятие функции Приближенные методы вычислений
Приближенные методы вычислений Решение задач по теории вероятности
Решение задач по теории вероятности Как нарисовать многоконечную звезду
Как нарисовать многоконечную звезду Угол между прямыми
Угол между прямыми Презентация по математике "Замысловатые маршруты Эйлера" - скачать
Презентация по математике "Замысловатые маршруты Эйлера" - скачать  Деление
Деление Жазықтықтағы және кеңістіктегі тікбұрышты координаталар. Векторлар және оларға қолданылатын сызықтық амалдар
Жазықтықтағы және кеңістіктегі тікбұрышты координаталар. Векторлар және оларға қолданылатын сызықтық амалдар Дроби разные нужны, дроби разные важны! (6 класс)
Дроби разные нужны, дроби разные важны! (6 класс) Линейные уравнения 1-го порядка. Уравнения Бернулли
Линейные уравнения 1-го порядка. Уравнения Бернулли Ограничения в виде равенств и неравенств
Ограничения в виде равенств и неравенств Площадь круга
Площадь круга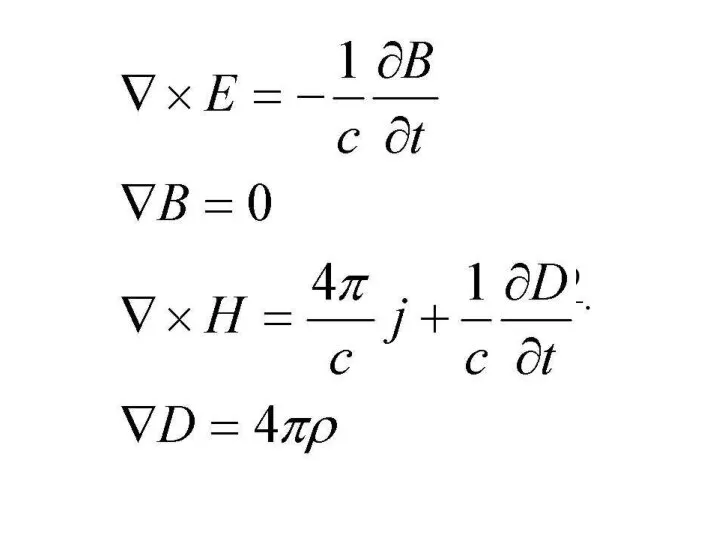 Система уравнений Максвелла дифференциальной и интегральной форм
Система уравнений Максвелла дифференциальной и интегральной форм Способы определения понятий
Способы определения понятий