Содержание
- 2. Первообразная Основное свойство первообразной Таблица первообразных Правила вычисления первообразных Интеграл Площадь криволинейной трапеции Вы познакомитесь в
- 3. УРОК 1
- 4. Функция F(x) называется первообразной функции f(x) на некотором промежутке, если для всех x из этого промежутка
- 5. Примеры f(x) = 2x; F(x) = x2 F′(x)= (x2)′ = 2x = f(x) f(x) = –
- 6. № 20.1-20.4 а,б 20.7 а,б
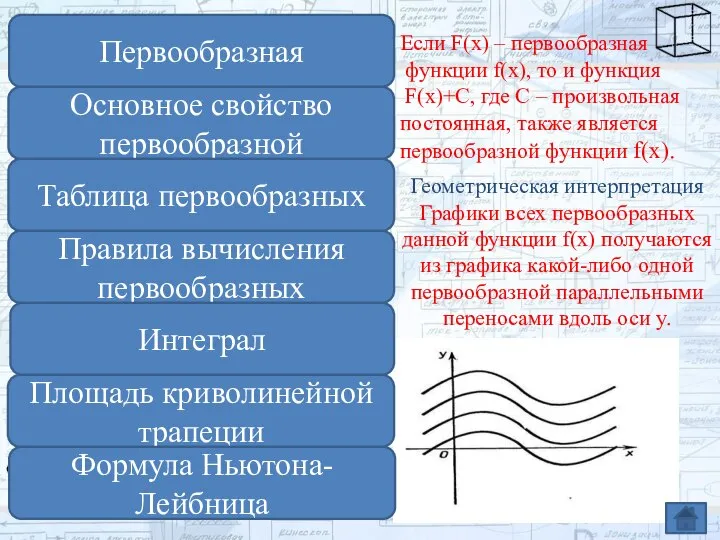
- 7. Если F(x) – первообразная функции f(x), то и функция F(x)+C, где C – произвольная постоянная, также
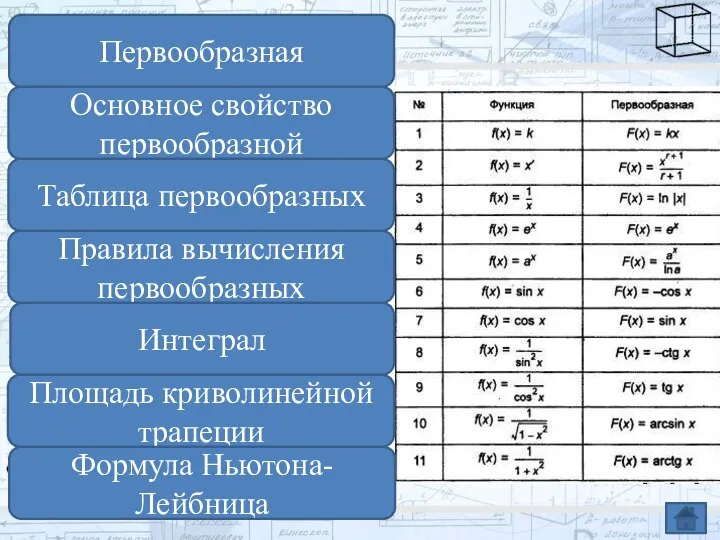
- 8. Первообразная Основное свойство первообразной Таблица первообразных Правила вычисления первообразных Интеграл Площадь криволинейной трапеции Формула Ньютона-Лейбница
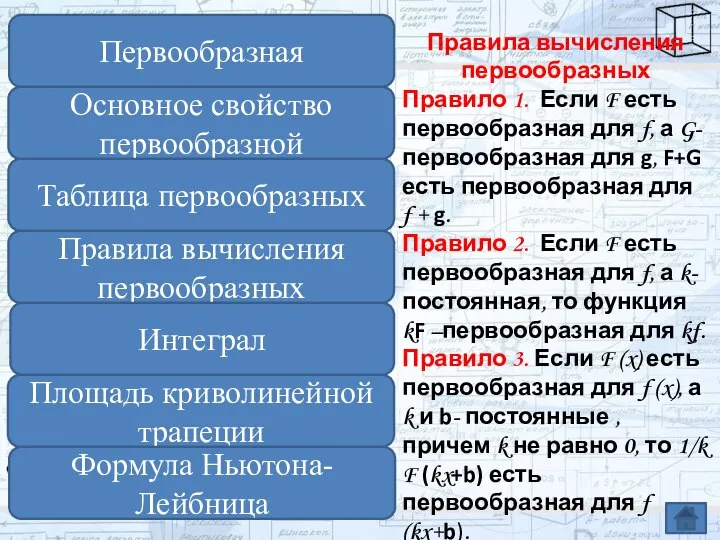
- 9. Правила вычисления первообразных Правило 1. Если F есть первообразная для f, а G-первообразная для g, F+G
- 10. УРОК 2 № 20.10 -20.17 а,б
- 11. № 20.20 -20.21 а,б № 20.25 -20.26 а,б УРОК 3
- 12. № 20.28 № 20.30 № 20.32 № 20.33 № 20.35-20.39 УРОК 3
- 13. Вычисление первообразной заключается в нахождении неопределенного интеграла, а сам процесс называется интегрированием Определение: Множество всех первообразных
- 14. Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных частей. Проведем через полученные точки прямые,
- 15. Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x), осью x и прямыми
- 16. Вычисление определенного интеграла
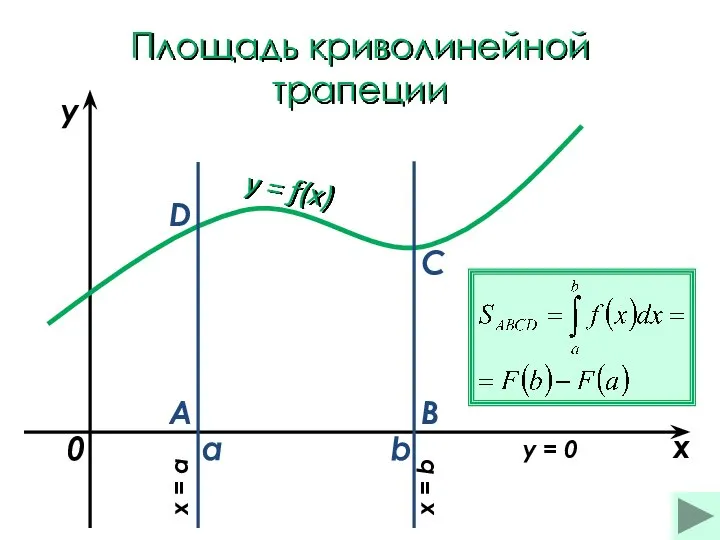
- 17. Площадь криволинейной трапеции a b x y y = f(x) 0 A B C D x
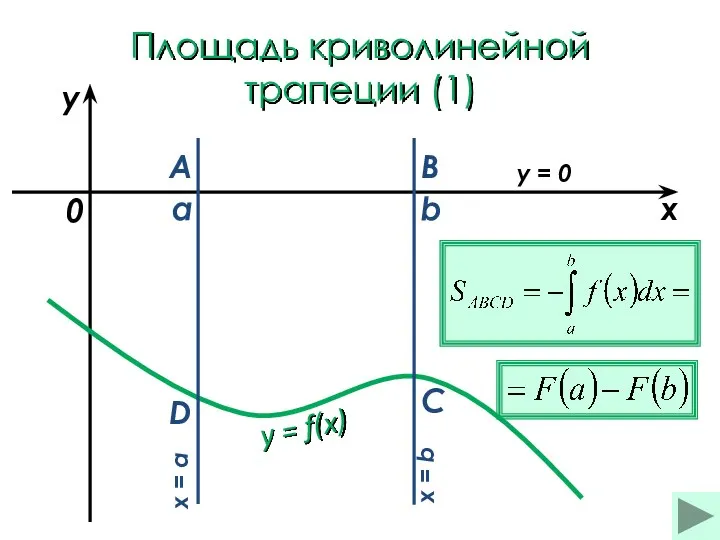
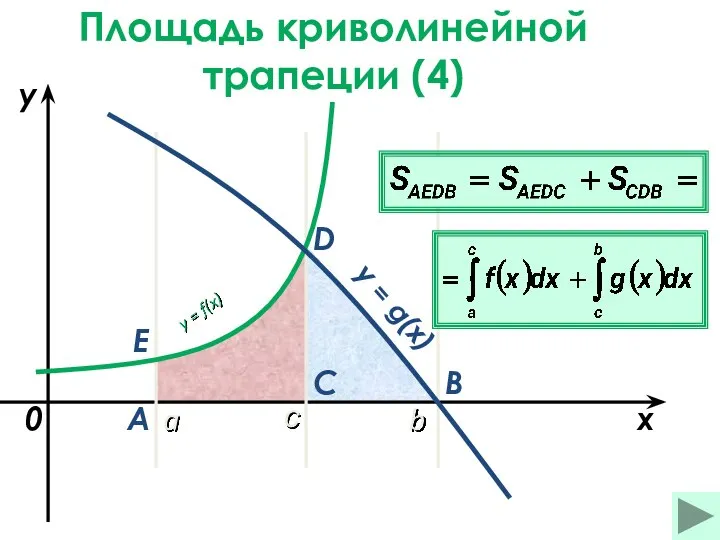
- 18. Площадь криволинейной трапеции (1) a b x y y = f(x) 0 A B C D
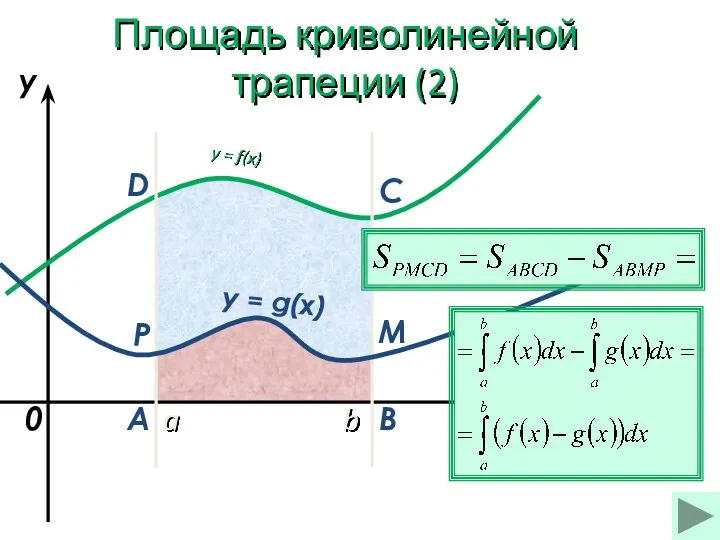
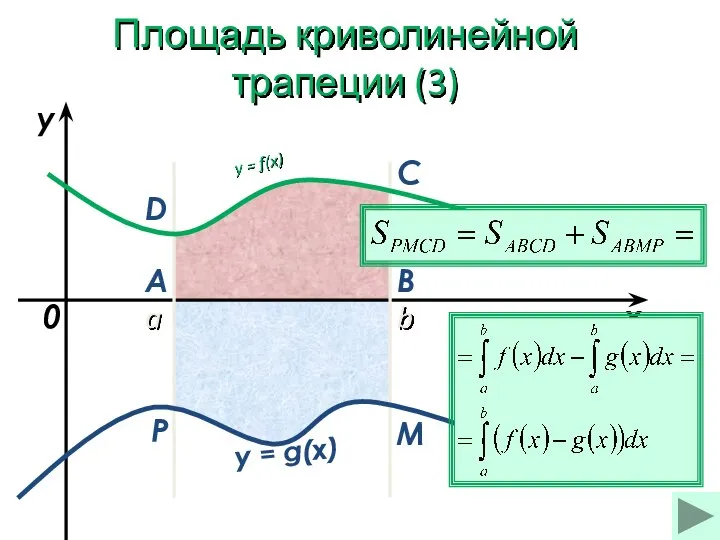
- 19. a b x y y = f(x) 0 y = g(x) A B C D M
- 20. a b x y y = f(x) 0 y = g(x) A B C D M
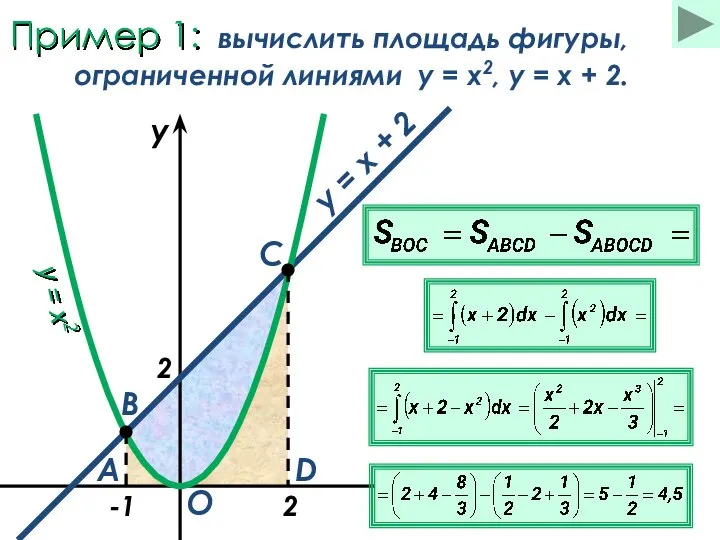
- 21. Пример 1: вычислить площадь фигуры, ограниченной линиями y = x2, y = x + 2. x
- 22. a b x y y = f(x) 0 y = g(x) A B C D с
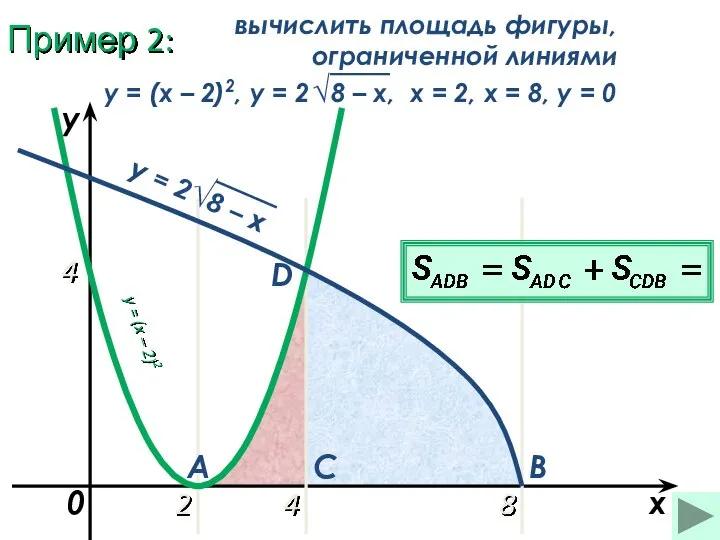
- 23. Пример 2: 2 8 x y = (x – 2)2 0 A B C D 4
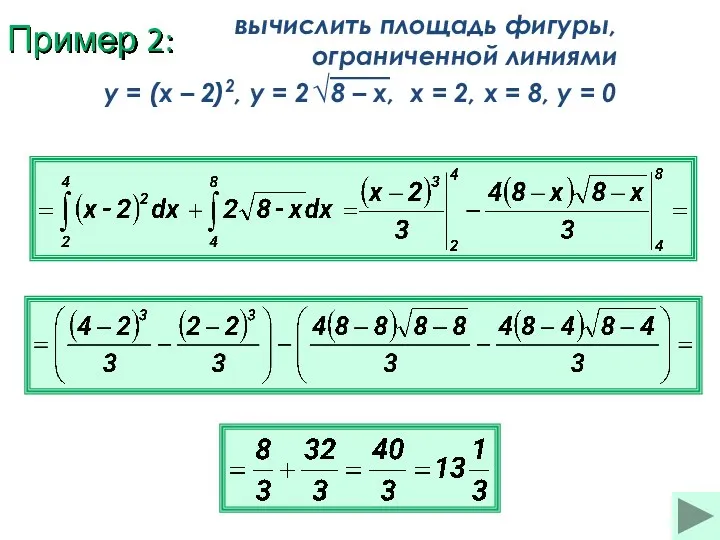
- 24. Пример 2:
- 26. Скачать презентацию









![Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных частей.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1448857/slide-13.jpg)
![Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1448857/slide-14.jpg)

 Сходимость знакоположительных рядов
Сходимость знакоположительных рядов Площади плоских фигур
Площади плоских фигур Решето Эратосфена
Решето Эратосфена Взаимные положения прямой и плоскости, двух плоскостей. Параллельность прямой и плоскости; двух плоскостей
Взаимные положения прямой и плоскости, двух плоскостей. Параллельность прямой и плоскости; двух плоскостей Математический бой. Конкурсы
Математический бой. Конкурсы «Математическая интерпретация эпидемии гриппа осенью 2009г. в г.Якутске». Выполнили: Буцык Катя, Полятинская Лиля, 6г класс МОУ СОШ
«Математическая интерпретация эпидемии гриппа осенью 2009г. в г.Якутске». Выполнили: Буцык Катя, Полятинская Лиля, 6г класс МОУ СОШ Задания В9
Задания В9 Особенности решения 22 задания (часть С) в ОГЭ - математика. Средняя скорость - это не среднее арифметическое чисел
Особенности решения 22 задания (часть С) в ОГЭ - математика. Средняя скорость - это не среднее арифметическое чисел Интегрирование на подмножествах (Кратный интеграл)
Интегрирование на подмножествах (Кратный интеграл) Координаты на прямой
Координаты на прямой Игра
Игра Математика әлеміне саяхат
Математика әлеміне саяхат Тест по теме: "Скалярное произведение векторов". Вариант 2
Тест по теме: "Скалярное произведение векторов". Вариант 2 Самостоятельная работа. Вычисление выражений
Самостоятельная работа. Вычисление выражений Нескучная математика
Нескучная математика Вычитание вида 50-24
Вычитание вида 50-24 Многогранники в биологии
Многогранники в биологии Подготовка к ЕГЭ Текстовые задачи на «смеси»
Подготовка к ЕГЭ Текстовые задачи на «смеси» Теория вероятностей, 9 класс.
Теория вероятностей, 9 класс.  Презентация по математике "Действия с положительными и отрицательными числами" - скачать бесплатно
Презентация по математике "Действия с положительными и отрицательными числами" - скачать бесплатно Теория вероятности. Основные категории теории вероятности
Теория вероятности. Основные категории теории вероятности Лекция № 11 Дискретное преобразование Фурье Дискретное преобразование Фурье (ДПФ) относится к классу основных преобразований пр
Лекция № 11 Дискретное преобразование Фурье Дискретное преобразование Фурье (ДПФ) относится к классу основных преобразований пр Задачка по математике Прогулка
Задачка по математике Прогулка Алгебра. Лекция 4. Количество и сумма натуральных делителей числа. Критерий простоты. Решето Эратосфена
Алгебра. Лекция 4. Количество и сумма натуральных делителей числа. Критерий простоты. Решето Эратосфена Урок математики Тема: «Квадратный дециметр» 3 класс
Урок математики Тема: «Квадратный дециметр» 3 класс  Свойства степени с натуральным показателем. 7 класс
Свойства степени с натуральным показателем. 7 класс Конкурсный урок геометрии в 7 классе. Тема урока «Треугольники»
Конкурсный урок геометрии в 7 классе. Тема урока «Треугольники» Длина окружности
Длина окружности