Содержание
- 2. Аналізу параметричної чуттєвості Післяоптимізаційний аналіз, або аналіз чуттєвості полягає у зв’язуванні впливу структурних, параметричних та структурно-параметричних
- 3. Рис. 1. Графічна ілюстрація алгоритму визначення меж зміни співвідношення між c1 та c2 у виразі для
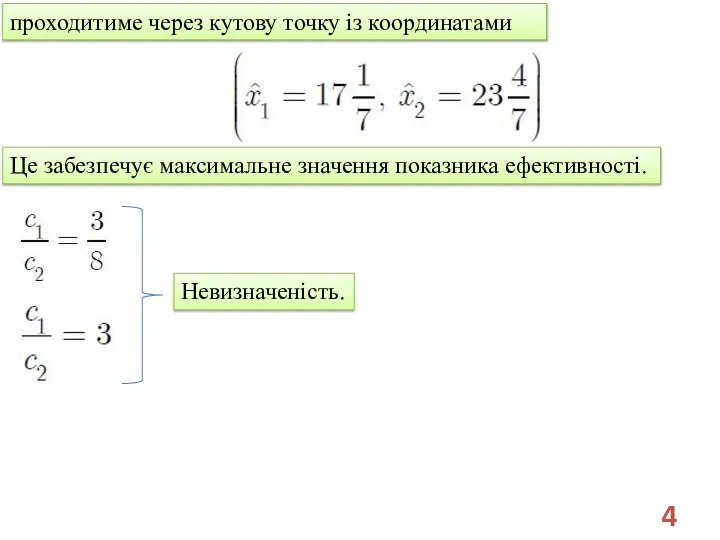
- 4. проходитиме через кутову точку із координатами Це забезпечує максимальне значення показника ефективності. Невизначеність.
- 5. З фізичної точки зору означає відповідно недоцільність випуску супутників зв’язку, або навігаційних супутників. При зміні співвідношення
- 6. Зрозуміло, що взагалі зміна будь-якого параметра математичної моделі задачі лінійного програмування (об’єм ресурсів та їх вартість),
- 7. Для дослідження впливу властивостей задачі лінійного програмування на її оптимальне за вихідною постановкою рішення в загальному
- 8. Ідея фізичного змісту побудови математичної моделі двоїстої задачі лінійного програмування Було поставлено за мету отримати максимальний
- 9. Задача лінійного програмування із змінними u1,2,3 формулюється так: якою повинна бути вартість кожного окремого ресурсу для
- 10. Загальна постановка і правила побудови двоїстої задачі
- 11. Кожній задачі лінійного програмування можливо поставити у відповідність задачу, яку називають двоїстою до неї. Припустимо, що
- 12. Задача двоїста до основної задачі – будується за наступними правилами: 1. Виконується впорядкування вихідної задачі до
- 13. 4. Матриця коефіцієнтів двоїстої задачі може бути отримана транспонуванням матриці A= ||ai,j||m×n, складеної із коефіцієнтів при
- 14. Пряму і двоїсту задачі лінійного програмування можливо записати у вигляді: Пряма та двоїста задача. Розглянемо двоїсту
- 15. Після перетворення, можемо записати: Висновок: 1) Двоїста задача лінійного програмування до двоїстої задачі лінійного програмування є
- 16. Приклад 1. Необхідно побудувати двоїсту задачу лінійного програмування. Приведемо задану задачу лінійного програмування до вигляду (1).
- 18. Двоїста ЗЛП набуває вигляду:
- 19. Побудувати двоїсту задачу. Приклад 2. Приведемо пряму задачу до стандартного вигляду.
- 20. Двоїста задача набуває вигляду:
- 21. Побудувати задачу двоїсту до заданої задачі лінійного програмування. Приклад 3.
- 22. Основні теореми двоїстості Теорема 1. Зауваження 1. Якщо показник ефективності однієї із задач необмеженний, то інша
- 23. Наслідок 1.
- 24. Теорема 2. Зауваження 2. Теорема 2 ще має назву «умова доповняльної нежорсткості» і формально записується у
- 25. Теорема 3.
- 26. Покажемо, що при зміненні правих частин bi(i=1,m) обмежень прямої задачі невідомі двоїстої задачі можливо інтерпретувати як
- 27. 2. Пряма та двоїста відповідно. Вимога, яка полягає в тому, що ΔB → 0 , означає,
- 29. Скачать презентацию

























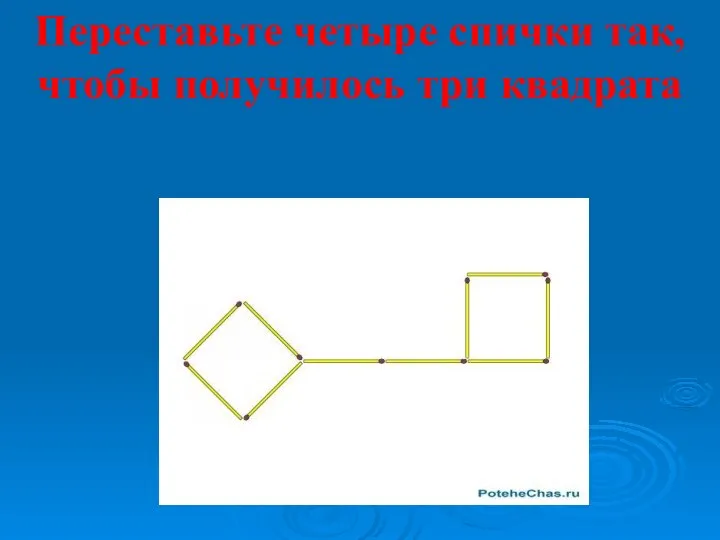 Игры со спичками
Игры со спичками Поиски математики. Игра
Поиски математики. Игра Первообразная. Основное свойство первообразной
Первообразная. Основное свойство первообразной Классы Фиттинга с заданными свойствами операторов Локетта
Классы Фиттинга с заданными свойствами операторов Локетта Решение задач
Решение задач Сложение натуральных чисел и его свойства
Сложение натуральных чисел и его свойства Теория надежности. Основные понятия и определения. (Лекция 1)
Теория надежности. Основные понятия и определения. (Лекция 1) Табличное решение логических задач
Табличное решение логических задач Весёлая матиматека
Весёлая матиматека Решение квадратных уравнений
Решение квадратных уравнений Умножение на 11
Умножение на 11 5 класс.
5 класс.  Задача на вычисление производной
Задача на вычисление производной Технология личностно-ориентированного обучения на уроках математики путем индивидуализации и дифференциации обучения
Технология личностно-ориентированного обучения на уроках математики путем индивидуализации и дифференциации обучения Простейшие задачи в координатах
Простейшие задачи в координатах МОУ «Средняя школа №17 г.Калуги» 10 «Б» класс Пидриксон Владислав Александрович представляет.
МОУ «Средняя школа №17 г.Калуги» 10 «Б» класс Пидриксон Владислав Александрович представляет. Понятие вектора
Понятие вектора Контроль знаний учащихся на уроках математики
Контроль знаний учащихся на уроках математики Приложения определенного интеграла к решению физических задач
Приложения определенного интеграла к решению физических задач Координатны вектора. Разложение вектора по координатным векторам
Координатны вектора. Разложение вектора по координатным векторам Математическая викторина для обучающихся 5-6 классов
Математическая викторина для обучающихся 5-6 классов Решение задач на применение первого признака равенства треугольников
Решение задач на применение первого признака равенства треугольников Построение сечений многогранников
Построение сечений многогранников Весёлая геометрия
Весёлая геометрия Дивергентные математические задачи как средство развития креативности мышления у младших школьников
Дивергентные математические задачи как средство развития креативности мышления у младших школьников Программа «Школа России» 2 класс (1-4) УРОК – ИГРА Тема: Сложение и вычитание в пределах 100 (устные вычисления)
Программа «Школа России» 2 класс (1-4) УРОК – ИГРА Тема: Сложение и вычитание в пределах 100 (устные вычисления)  Стереометрія. Аксіоми стереометрії
Стереометрія. Аксіоми стереометрії Математические головоломки
Математические головоломки