Площадь криволинейной трапеции

ПОВТОРИМ!

1. Функция F(х) называется первообразной функции f(x) на некотором промежутке, если

Таблица первообразных

Правила нахождения первообразных

Найдите первообразную функции

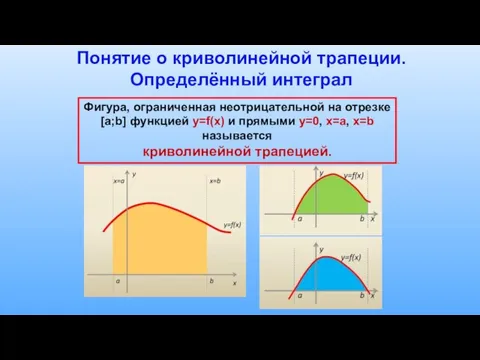
Понятие о криволинейной трапеции. Определённый интеграл

Фигура, ограниченная неотрицательной на отрезке [a;b]

Криволинейная трапеция

Отрезок [a;b] -основание
этой криволинейной трапеции

Опр. Криволинейной трапецией

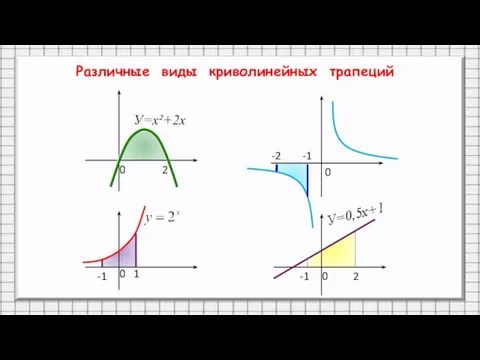
Различные виды криволинейных трапеций

0

2

0

0

0

1

-1

-1

2

-1

-2

У=х²+2х

У=0,5х+1

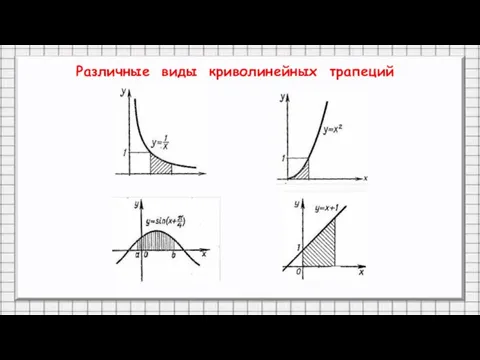
Различные виды криволинейных трапеций

у

у

у

у

у

у

У=1

3

y = f(x)

y = f(x)

y = f(x)

y = f(x)

y = f(x)

y

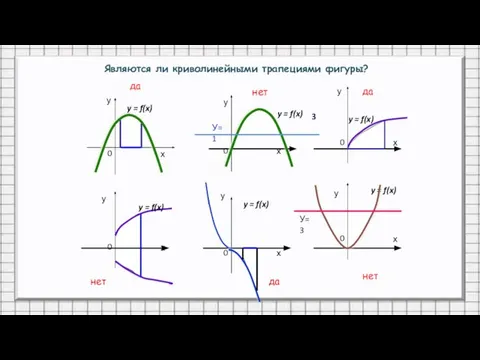
Самостоятельно решить:

Лист 1

ЗАДАНИЕ 1.

Указать фигуры, которые являются криволинейными трапециями

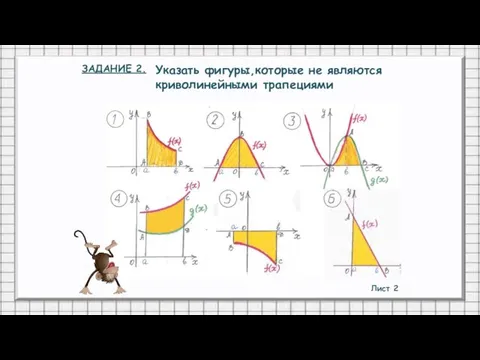
Лист 2

ЗАДАНИЕ 2.

Указать фигуры,которые не являются криволинейными трапециями

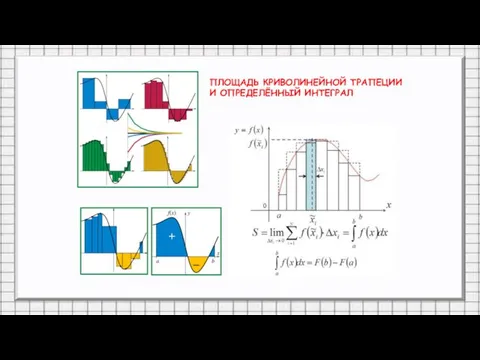
ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ
И ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

Формула Ньютона - Лейбница

Исаак Ньютон
1642-1727

Готфрид Лейбниц
1646-1716 гг.

Таким образом:

Геометрический смысл интеграла

Определённый интеграл от неотрицательной непрерывной функции f(x) по [a, b] численно равен площади криволинейной трапеции с

Физический смысл интеграла

Материальная точка движется по прямой со скоростью, определяемой формулой

ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ФИГУР
С ПОМОЩЬЮ ОПРЕДЕЛЁННОГО
ИНТЕГРАЛА

Вычисление площадей с помощью интегралов

1. Криволинейная трапеция, ограниченная сверху графиком функции

2. Фигура, ограниченная сверху только графиком функции y=f(x) и снизу осью

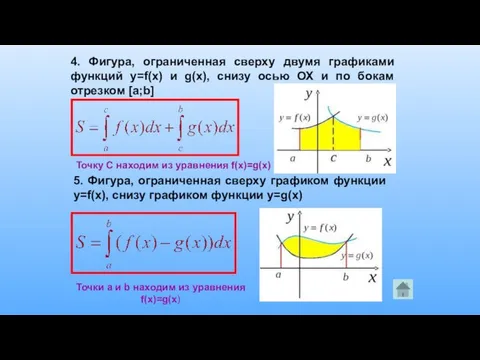
4. Фигура, ограниченная сверху двумя графиками функций y=f(x) и g(x), снизу

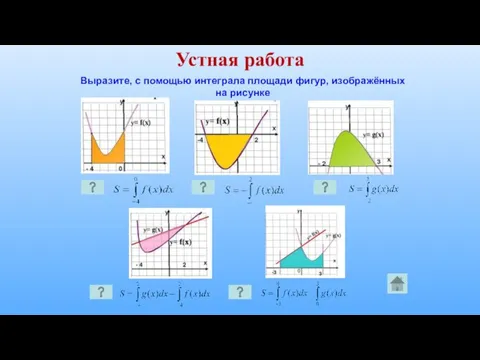
Устная работа

Выразите, с помощью интеграла площади фигур, изображённых на рисунке

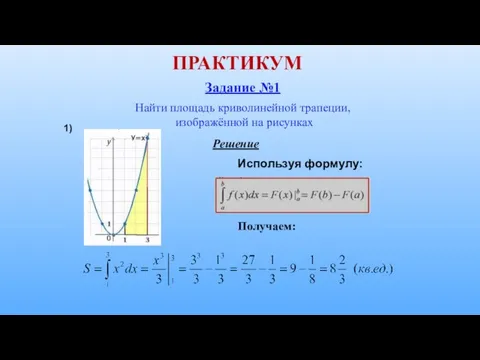
ПРАКТИКУМ

Задание №1
Найти площадь криволинейной трапеции,
изображённой на рисунках

Используя формулу:

Решение

Получаем:

1)

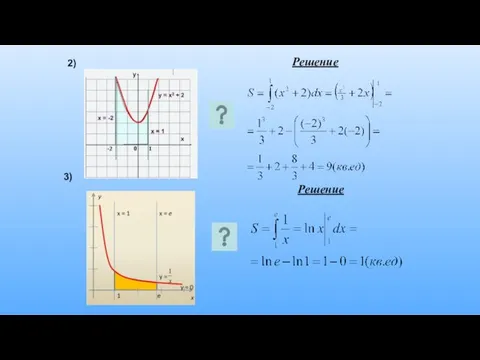
2)

Решение

3)

Решение

4)

Решение

5)

Решение

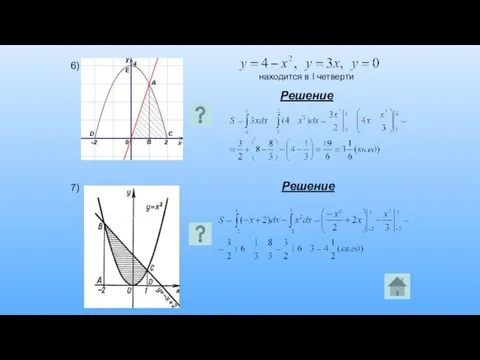
6)

находится в I четверти

Решение

7)

Решение

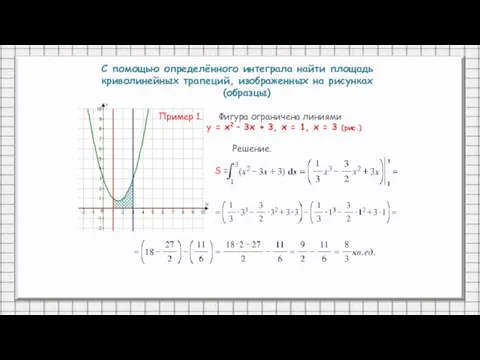
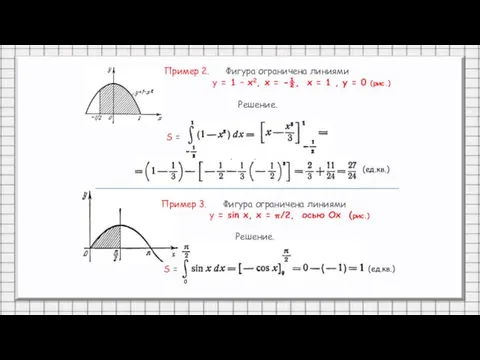
С помощью определённого интеграла найти площадь
криволинейных трапеций, изображенных на рисунках

Пример 2. Фигура ограничена линиями
у = 1 – х2, х

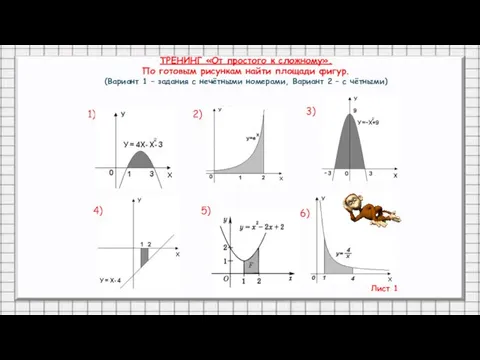
ТРЕНИНГ «От простого к сложному». По готовым рисункам найти площади фигур. (Вариант 1

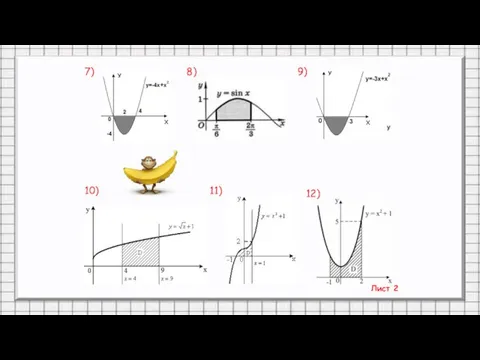
7)

8)

9)

10)

11)

12)

Лист 2

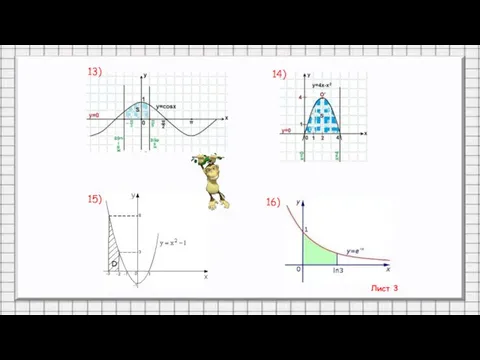
Лист 3

13)

14)

15)

16)

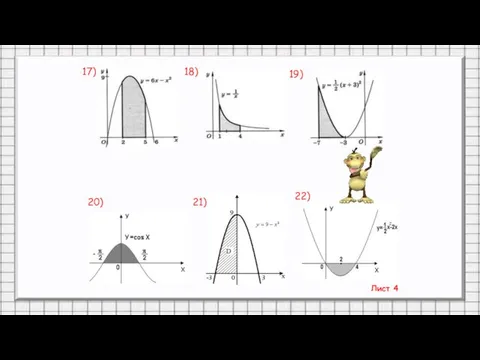
Лист 4

17)

18)

19)

20)

21)

22)

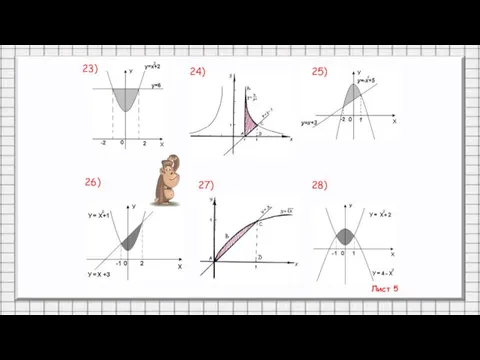
Лист 5

23)

24)

25)

26)

27)

28)

Лист 6

30)

31)

32)

33)

34)

29)

По готовым рисункам найти площади фигур , составив комбинации площадей

Вычислите площадь фигуры, ограниченной линиями (схематично изобразив графики функций).

Ответ: 1) 4,5

Контрольные вопросы:

Какая функция называется первообразной для функции f(x)?
Чем отличаются друг от

Домашнее задание

Вычислить площадь фигуры, ограниченной линиями, предварительно сделав рисунок

Подведём итоги
Познакомились с понятиями криволинейной трапеции и определённого интеграла.
Научились вычислять

Список используемых источников

Алимов Ш.А., Колягин Ю.М., Ткачёва М.В. и др. Алгебра