Если бы движение было равномерным, то задача решалась бы очень просто:
s = vt, т.е. s = v(b-a). Для неравномерного движения приходится использовать те же идеи, на которых было основано решение предыдущей задачи.
Разобьём отрезок [а; b] на n равных частей.
Рассмотрим отдельно k-ый участок [tk; tk+1] и будем считать, что скорость на этом промежутке времени постоянна, а именно такая, как, например, в момент времени tk . Итак, считаем, что v = v(tk).
Найдём приближённое значение перемещения точки sk за промежуток времени [tk ; tk+1]:
sk ≈ v(tk)·Δ tk,
4) Найдём приближённое значение перемещения s:
s ≈ Sn, где Sn= s 0 + s 1 + s 2 + … + s k + … + s n-1 =
v(t0)Δt0 + v(t1)Δt1 + v(t2)Δt2 + … + v(tk)Δtk + … + v(tn-1)Δtn-1.
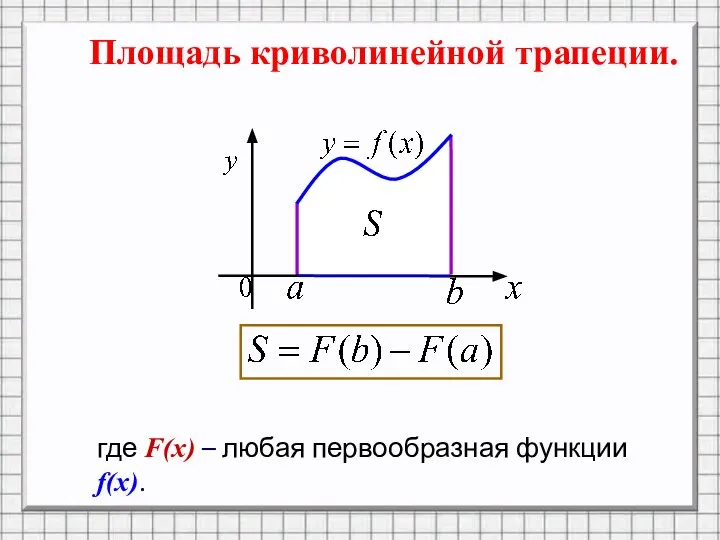
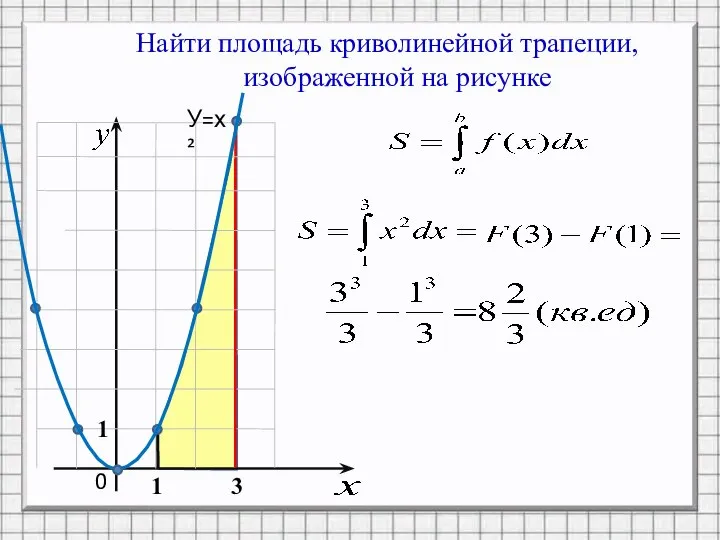
5) Точное значение перемещения вычисляется по формуле:
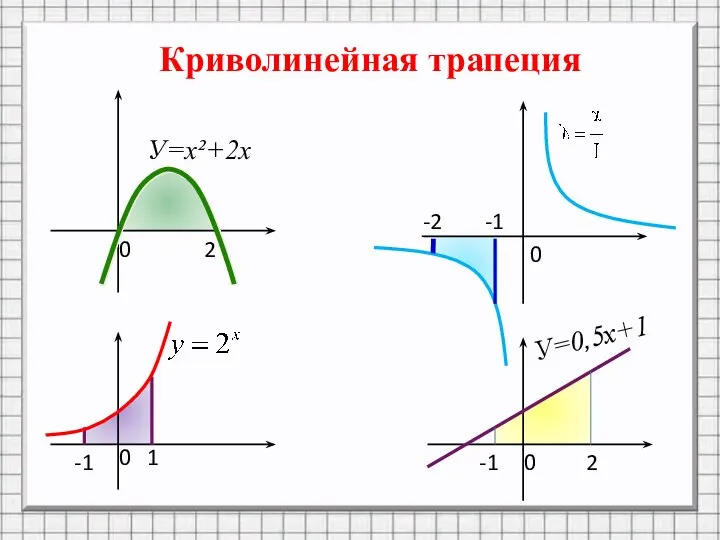
![Криволинейная трапеция Отрезок [a;b] называют основанием этой криволинейной трапеции Криволинейной трапецией](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1465741/slide-1.jpg)

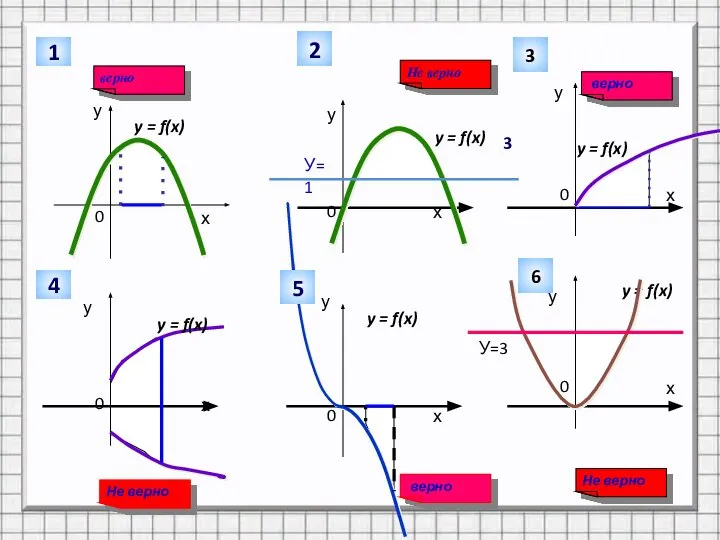
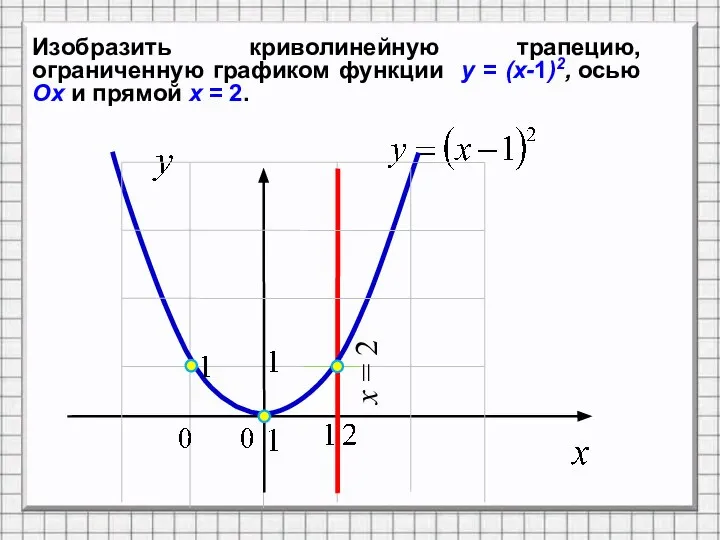



![Теорема. Если функция y = f(x) непрерывна на отрезке [а; b],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1465741/slide-9.jpg)
 Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Аттестационная работа. Организация проектной деятельности на уроках математики в основной школе
Аттестационная работа. Организация проектной деятельности на уроках математики в основной школе Булева алгебра
Булева алгебра Алгебра. Подготовка к контрольной работе
Алгебра. Подготовка к контрольной работе Дисперсионный анализ
Дисперсионный анализ Задачи на чертежах по теме трапеция
Задачи на чертежах по теме трапеция Аттестационная работа. Проектно – исследовательская деятельность на уроках математики
Аттестационная работа. Проектно – исследовательская деятельность на уроках математики Точка, линия, прямая и кривая линии. Число 2. Цифра 2
Точка, линия, прямая и кривая линии. Число 2. Цифра 2 Презентация по математике "Игра по математике: Считаем со Смешариками!" - скачать
Презентация по математике "Игра по математике: Считаем со Смешариками!" - скачать  Аттестационная работа. Курс дополнительного образования «Математическая эстафета»
Аттестационная работа. Курс дополнительного образования «Математическая эстафета» Область определения функции. Урок индивидуального обучения
Область определения функции. Урок индивидуального обучения Численные методы решения нелинейных уравнений и систем нелинейных уравнений
Численные методы решения нелинейных уравнений и систем нелинейных уравнений Презентация на тему Нахождение наибольшего и наименьшего значения функции
Презентация на тему Нахождение наибольшего и наименьшего значения функции  Геометрические характеристики плоских сечений
Геометрические характеристики плоских сечений Приёмы письменного деления на однозначное число
Приёмы письменного деления на однозначное число Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал
Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал Решение задач. Определение по графикам формулы функций
Решение задач. Определение по графикам формулы функций Определения многогранников. Теорема Эйлера
Определения многогранников. Теорема Эйлера Деление многозначного числа на однозначное
Деление многозначного числа на однозначное Кривые на плоскости
Кривые на плоскости Подготовка к ГИА. Решение задач обязательной части ГИА по геометрии. Задачи № 9, 10
Подготовка к ГИА. Решение задач обязательной части ГИА по геометрии. Задачи № 9, 10 Правильные многогранники
Правильные многогранники Степенева функція
Степенева функція Дидактическая игра как средство повышения эффективности урока математики
Дидактическая игра как средство повышения эффективности урока математики Геометрическая подготовка младшего школьника
Геометрическая подготовка младшего школьника Площадь трапеции. Свойства площадей
Площадь трапеции. Свойства площадей Десятичные дроби и метрическая система мер
Десятичные дроби и метрическая система мер Сравнение дробей. 5 класс
Сравнение дробей. 5 класс