Содержание
- 2. Подобные фигуры Предметы одинаковой формы, но разных размеров Фотографии, отпечатанные с одного негатива, но с разными
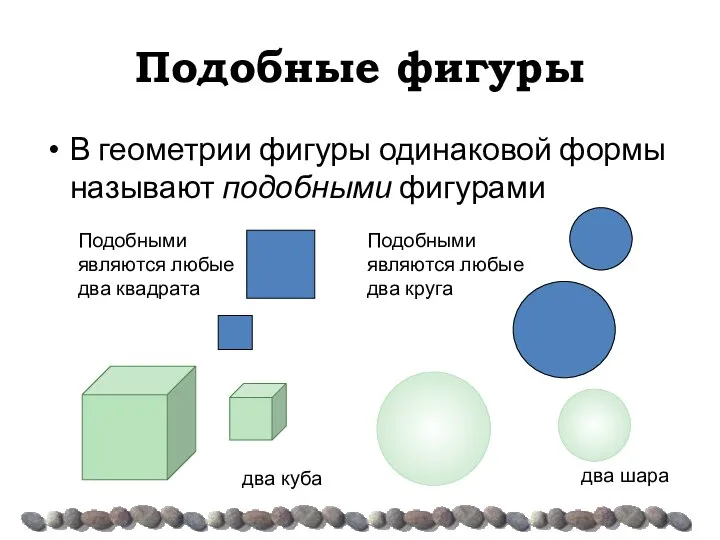
- 3. Подобные фигуры В геометрии фигуры одинаковой формы называют подобными фигурами Подобными являются любые два квадрата Подобными
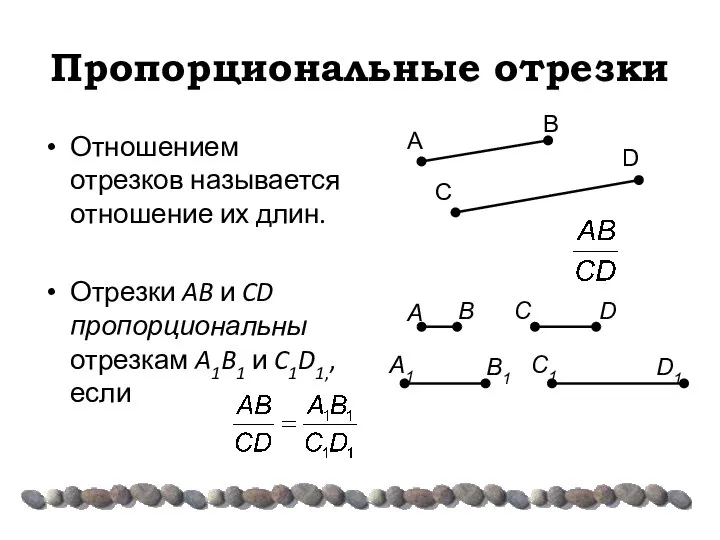
- 4. Пропорциональные отрезки Отношением отрезков называется отношение их длин. Отрезки AB и CD пропорциональны отрезкам A1B1 и
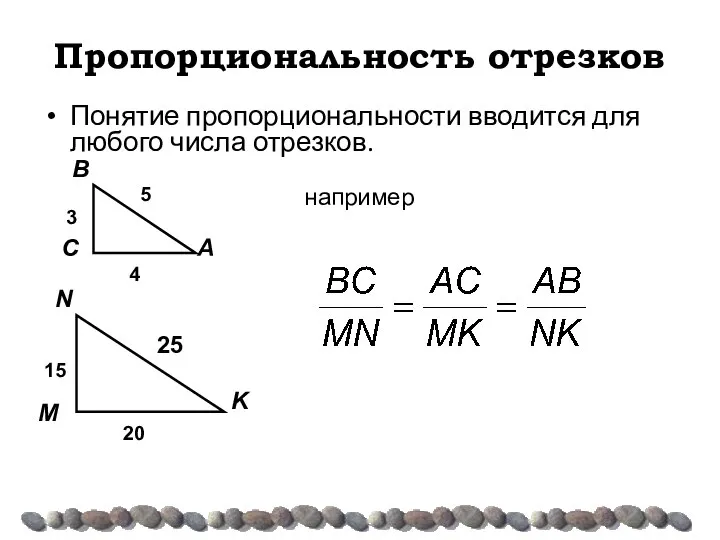
- 5. Пропорциональность отрезков Понятие пропорциональности вводится для любого числа отрезков. например
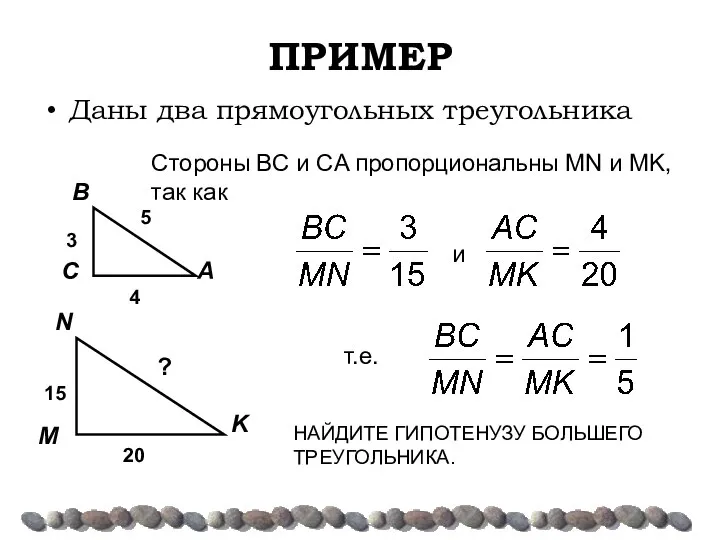
- 6. ПРИМЕР Даны два прямоугольных треугольника Стороны ΒC и CA пропорциональны MN и MK, так как т.е.
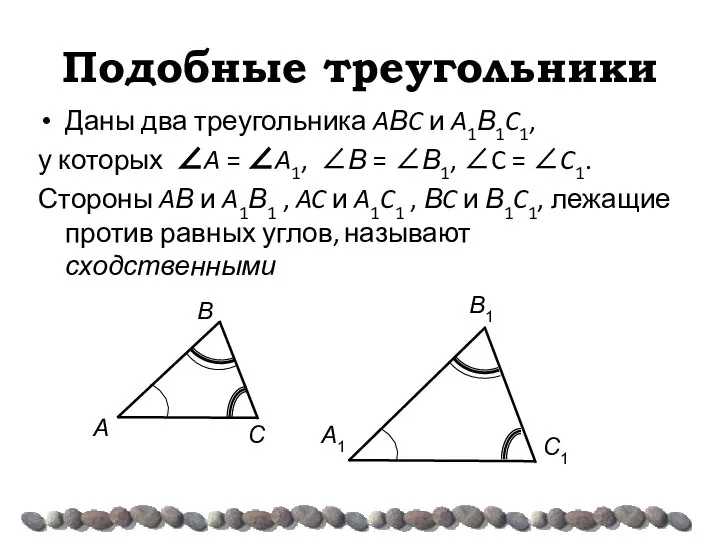
- 7. Подобные треугольники Даны два треугольника AΒC и A1Β1C1, у которых ∠A = ∠A1, ∠Β = ∠Β1,
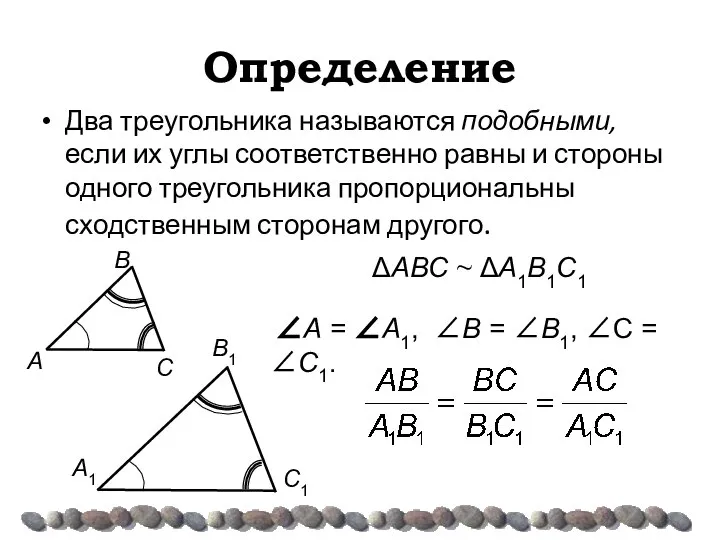
- 8. Определение Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным
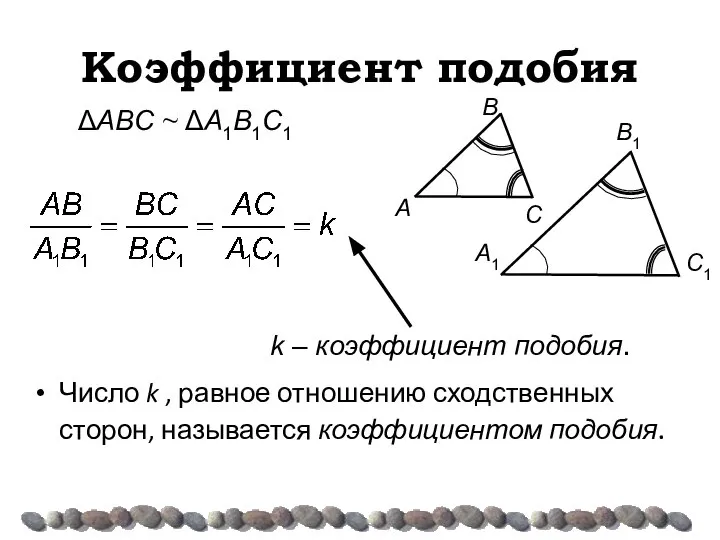
- 9. Коэффициент подобия Число k , равное отношению сходственных сторон, называется коэффициентом подобия. ΔAΒC ~ ΔA1Β1C1 k
- 10. Дополнительные свойства Отношение высот подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия. Отношение медиан подобных
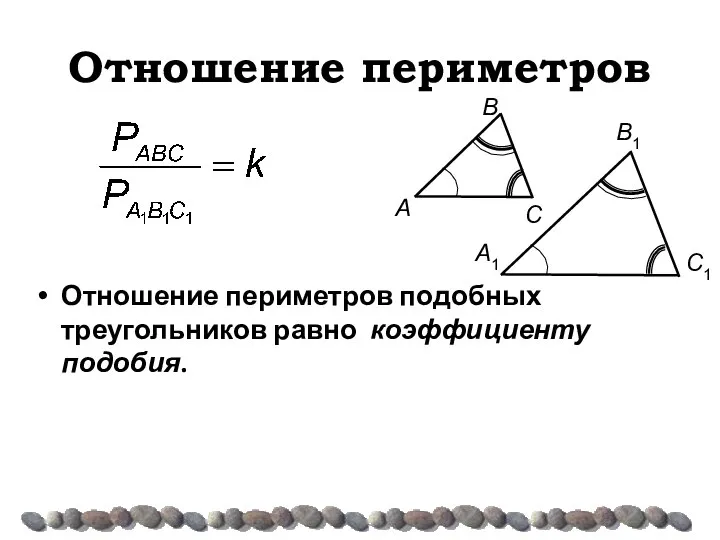
- 11. Отношение периметров Отношение периметров подобных треугольников равно коэффициенту подобия.
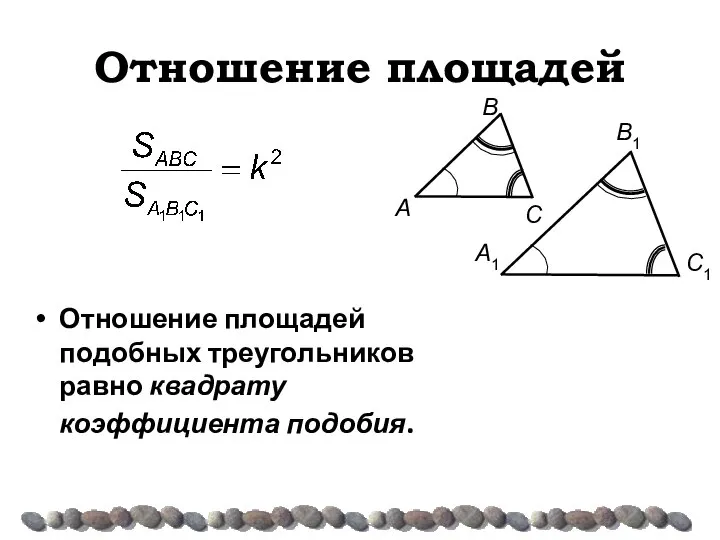
- 12. Отношение площадей Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
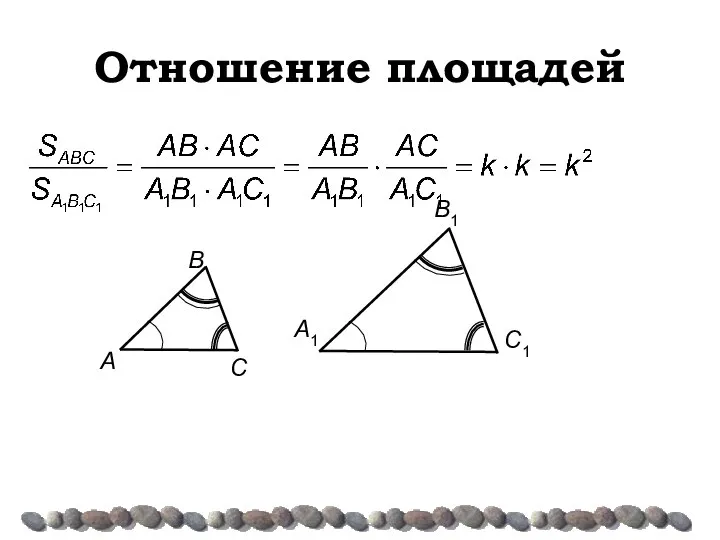
- 13. Отношение площадей
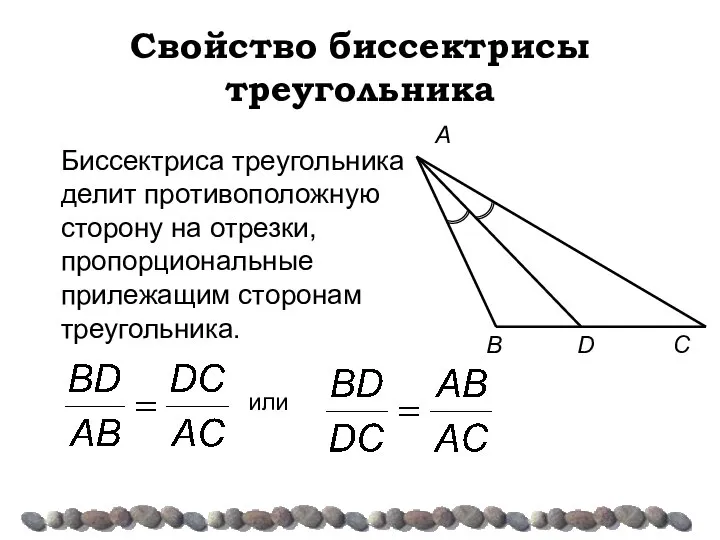
- 14. Свойство биссектрисы треугольника C B A Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам
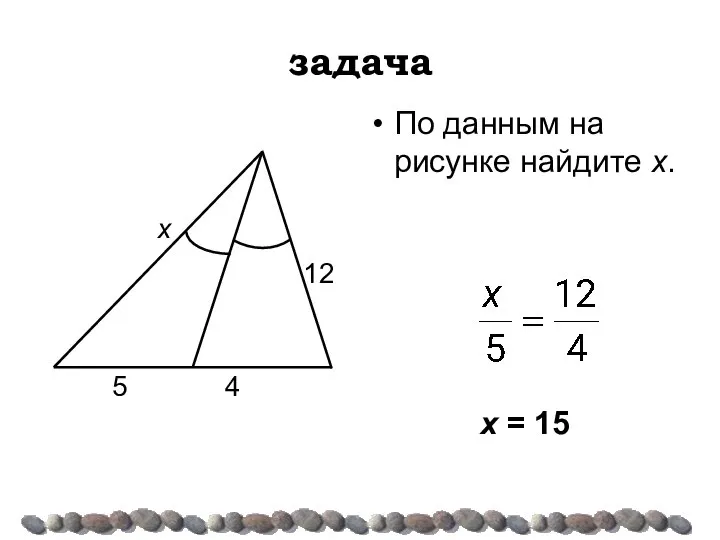
- 15. задача По данным на рисунке найдите х. х = 15
- 16. задача Отношение площадей двух квадратов равно 9 : 1. Найдите сторону большего их них, если сторона
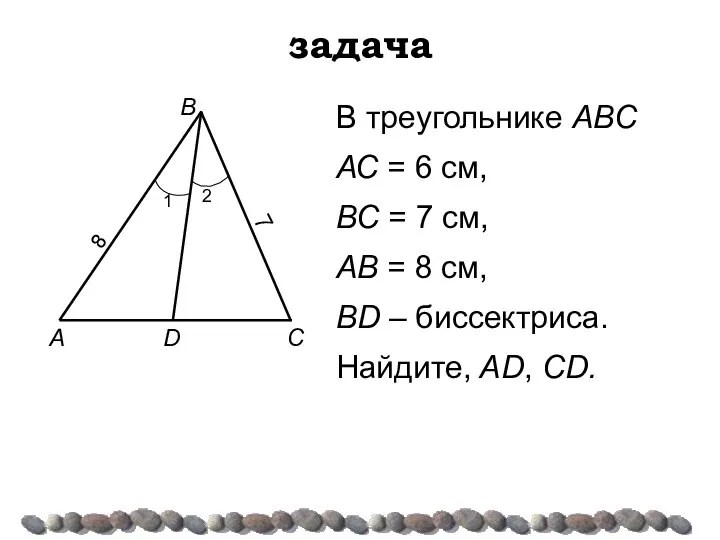
- 17. задача В треугольнике АВС АС = 6 см, ВС = 7 см, AB = 8 см,
- 18. задача Треугольник со сторонами 2 см, 3 см, 4 см подобен треугольнику со сторонами 5 мм,
- 19. задача Сходственные стороны подобных треугольников относятся как 1 : 3. Найдите периметр большего треугольника, если периметр
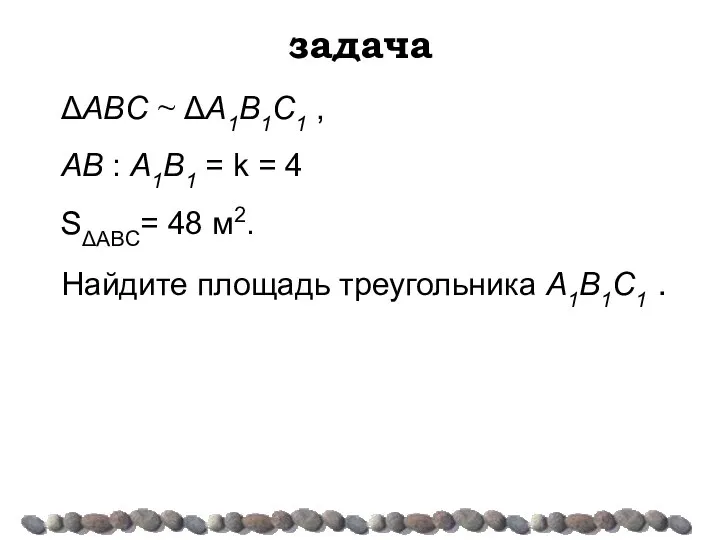
- 20. задача ΔABC ~ ΔA1B1C1 , AB : A1B1 = k = 4 SΔABC= 48 м2. Найдите
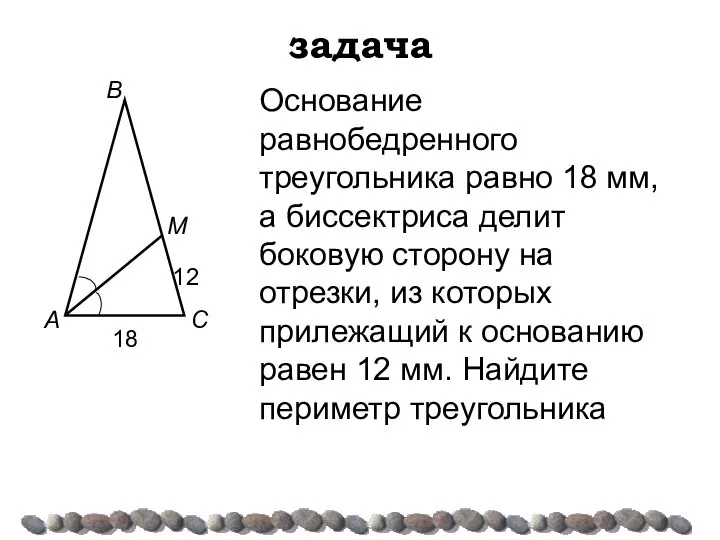
- 21. задача Основание равнобедренного треугольника равно 18 мм, а биссектриса делит боковую сторону на отрезки, из которых
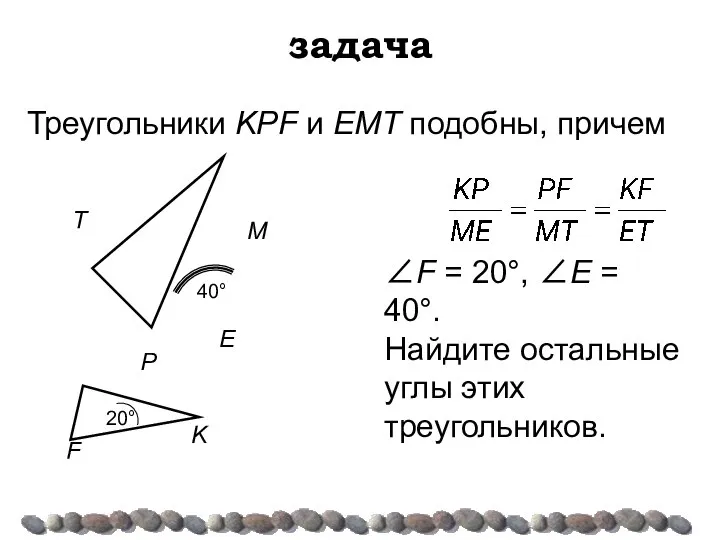
- 22. задача Треугольники KPF и ЕМТ подобны, причем ∠F = 20°, ∠E = 40°. Найдите остальные углы
- 23. задача Периметры подобных треугольников 12 мм и 108 мм соответственно. Стороны одного из них 3 мм,
- 24. задача Площади двух подобных треугольников равны 16 см2 и 25 см2. Одна из сторон первого треугольника
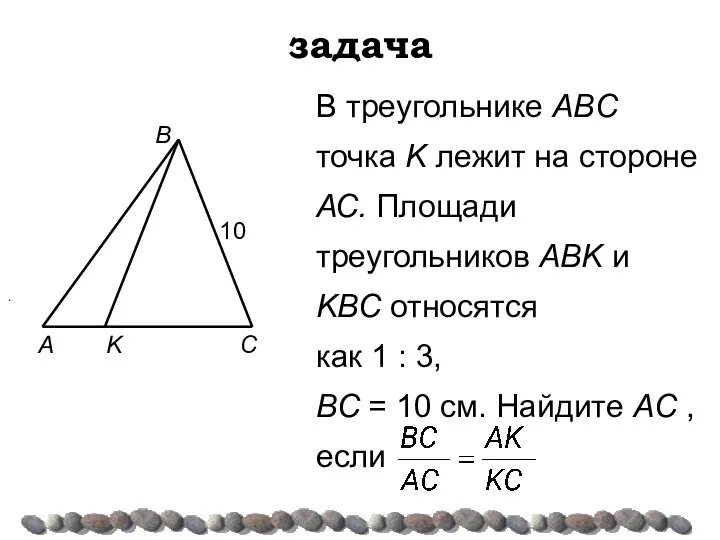
- 25. В треугольнике ABC точка K лежит на стороне АС. Площади треугольников АВK и KВС относятся как
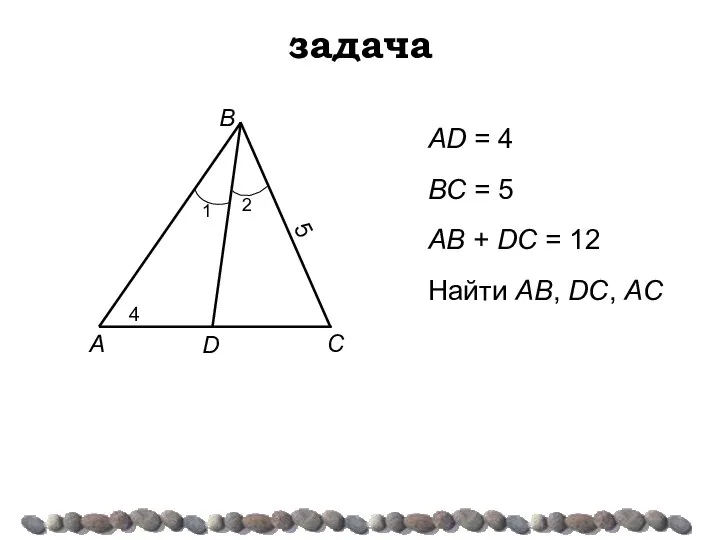
- 26. задача AD = 4 BC = 5 AB + DC = 12 Найти AB, DC, AC
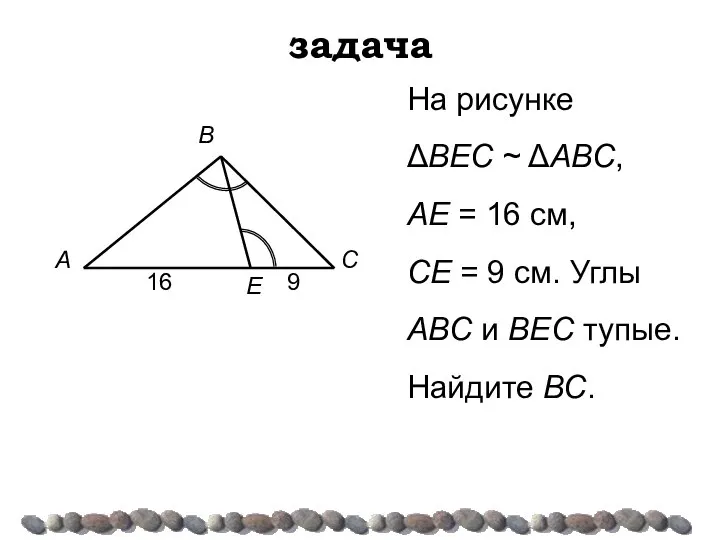
- 27. задача На рисунке ΔВЕС ~ ΔАВС, АЕ = 16 см, СЕ = 9 см. Углы ABC
- 28. задача Периметры подобных треугольников относятся как 2 : 3, сумма их площадей равна 260 см2. Найдите
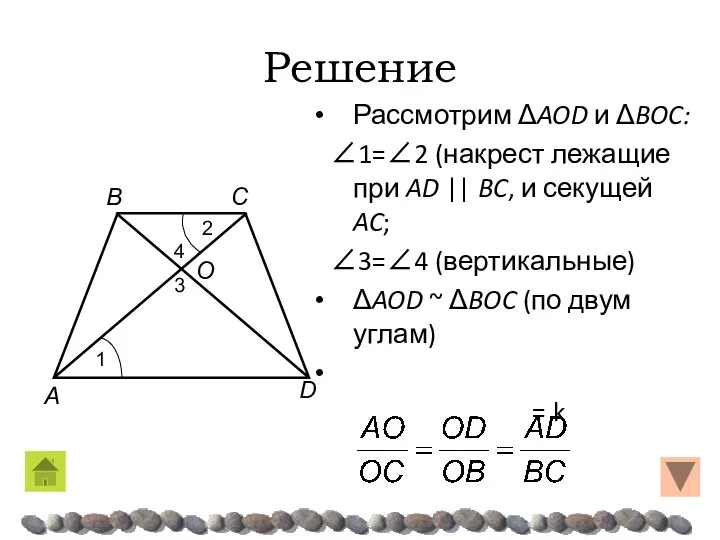
- 29. ЗАДАЧИ 1. Диагонали трапеции ABCD пересекаются в точке O. Площади треугольников BOC и AOD относятся как
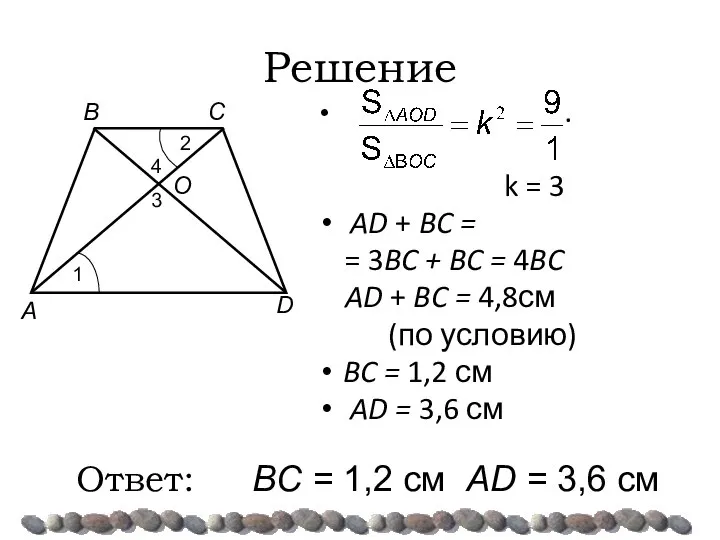
- 30. Решение Рассмотрим ΔAOD и ΔBOC: ∠1=∠2 (накрест лежащие при AD || BC, и секущей AC; ∠3=∠4
- 31. Решение . k = 3 AD + BC = = 3BC + BC = 4BC AD
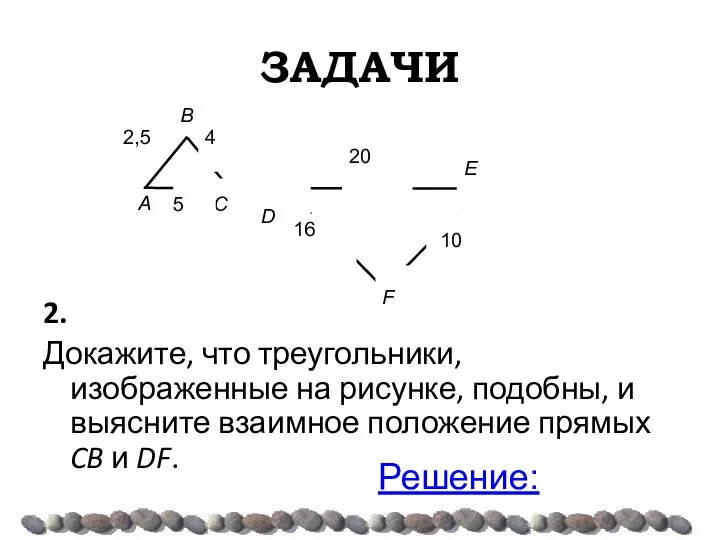
- 32. ЗАДАЧИ 2. Докажите, что треугольники, изображенные на рисунке, подобны, и выясните взаимное положение прямых CB и
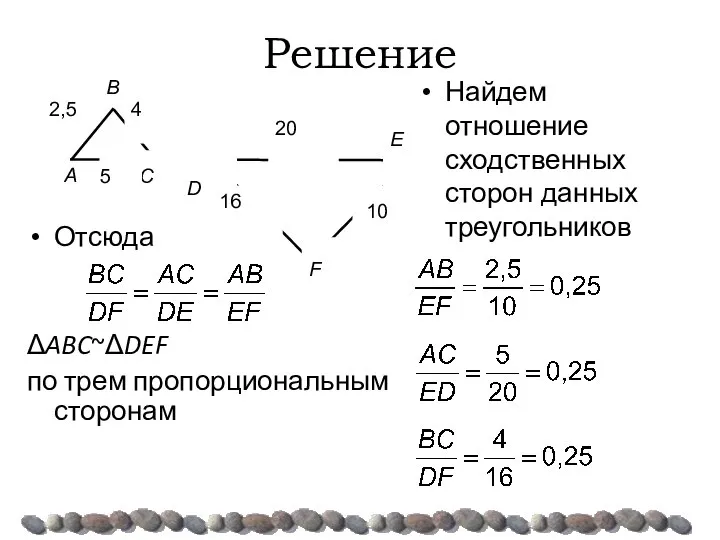
- 33. Решение Отсюда ΔABC~ΔDEF по трем пропорциональным сторонам Найдем отношение сходственных сторон данных треугольников
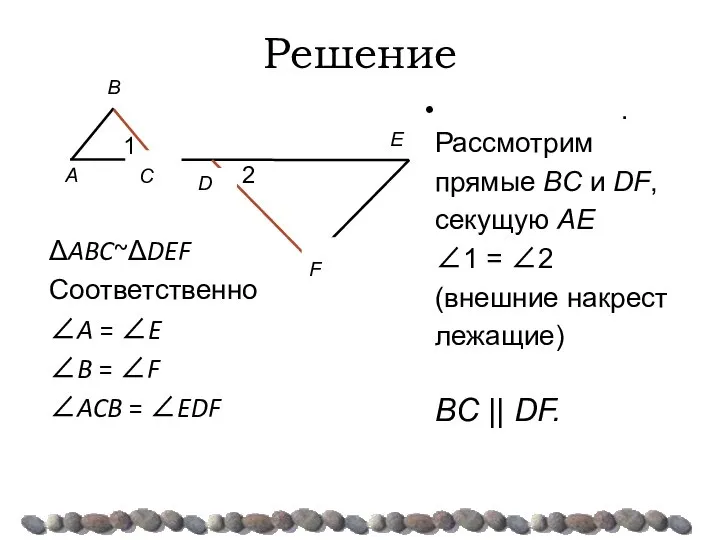
- 34. Решение ΔABC~ΔDEF Соответственно ∠A = ∠E ∠B = ∠F ∠ACB = ∠EDF E . Рассмотрим прямые
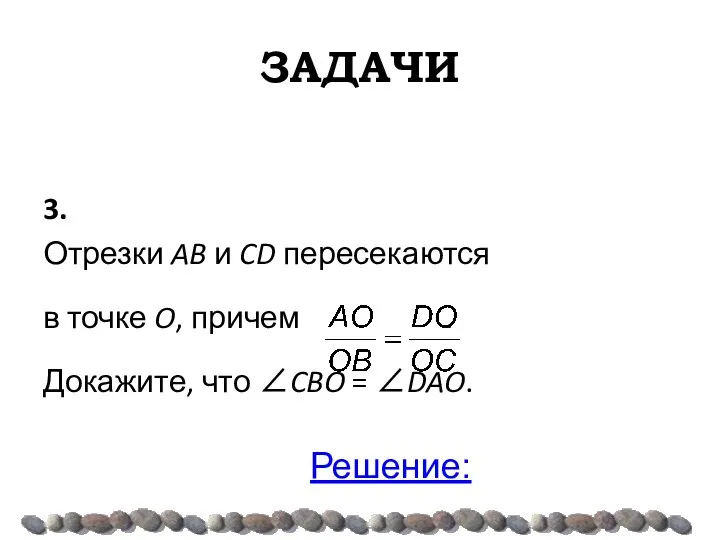
- 35. ЗАДАЧИ 3. Отрезки AB и CD пересекаются в точке O, причем . Докажите, что ∠CBO =
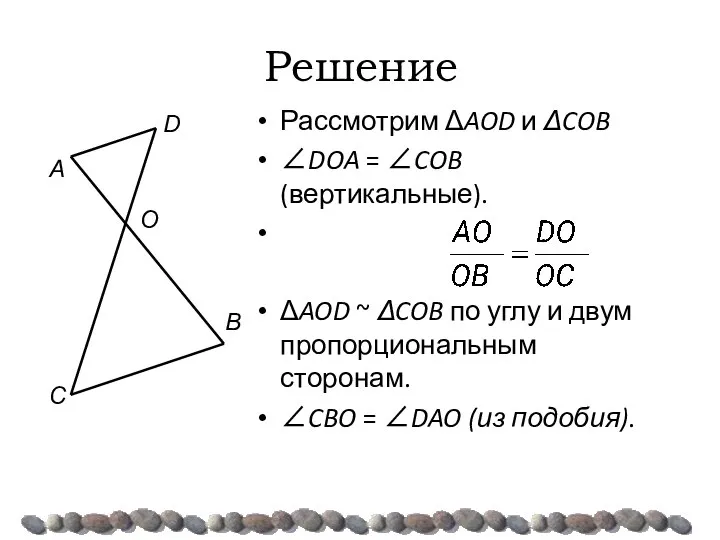
- 36. Решение Рассмотрим ΔAOD и ΔCOB ∠DOA = ∠COB (вертикальные). . ΔAOD ~ ΔCOB по углу и
- 37. ЗАДАЧИ 4. В треугольнике ABC AB = 4, BC = 6, AC = 7. Точка E
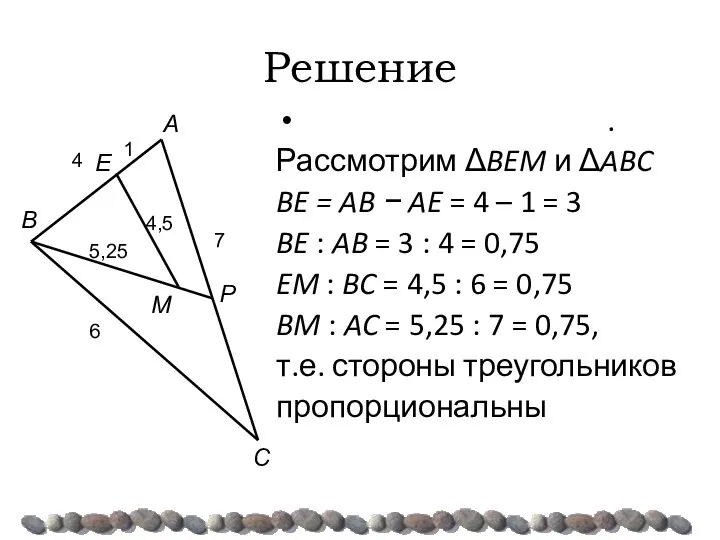
- 38. Решение . Рассмотрим ΔBEM и ΔABC BE = AB − AE = 4 – 1 =
- 39. ΔBEM ~ ΔABC по трем пропорциональным сторонам. Следовательно, ∠BME = ∠AСB ∠EBM = ∠BAC ∠BEM =
- 40. ЗАДАЧИ 5. Диагональ AC параллелограмма ABCD равна 90. Середина M стороны AB соединена с вершиной D.
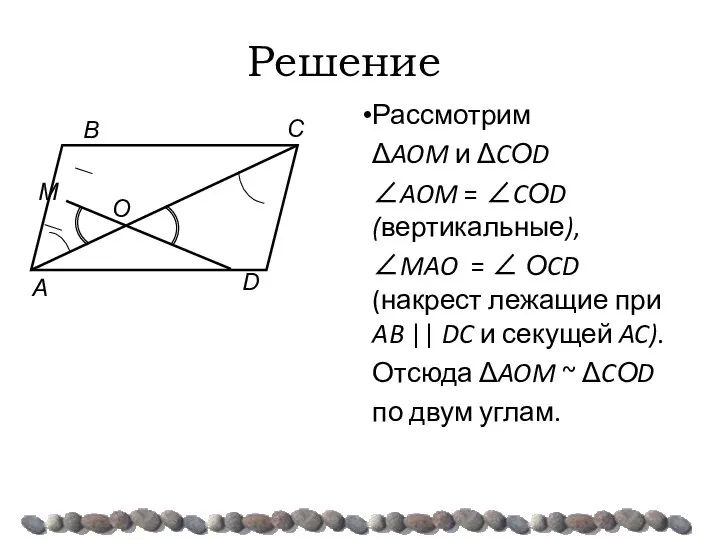
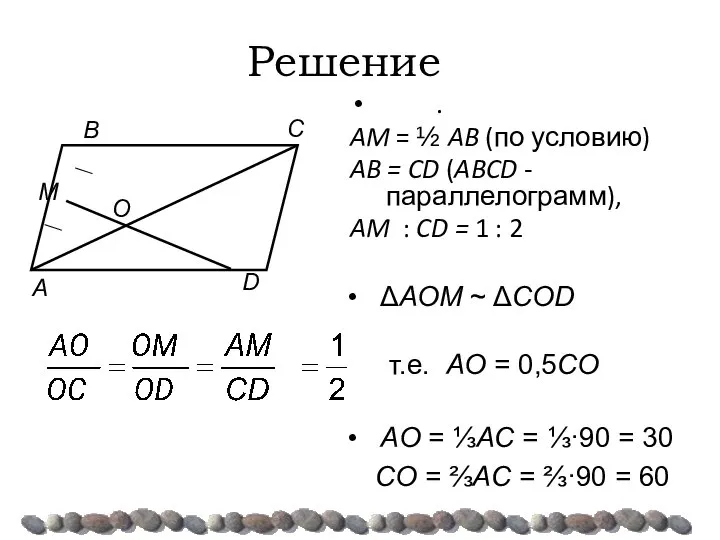
- 41. Решение Рассмотрим ΔAOM и ΔCОD ∠AOM = ∠CОD (вертикальные), ∠MAO = ∠ ОCD (накрест лежащие при
- 42. Решение . AM = ½ AB (по условию) AB = CD (ABCD - параллелограмм), AM :
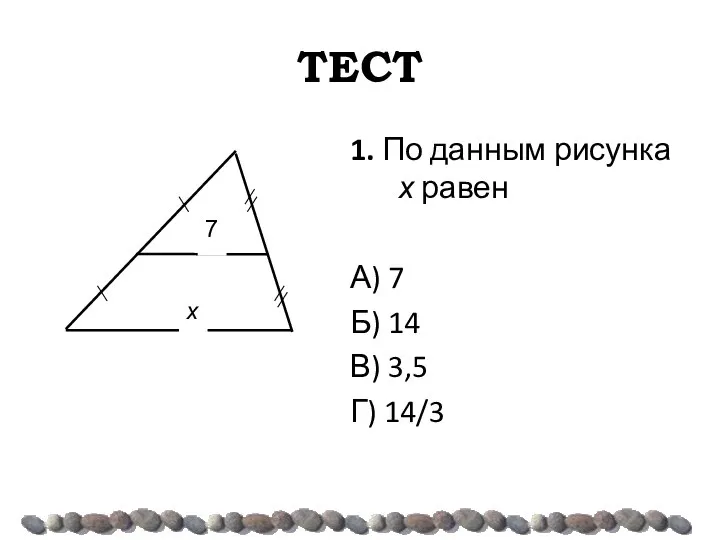
- 43. ТЕСТ 1. По данным рисунка х равен А) 7 Б) 14 В) 3,5 Г) 14/3
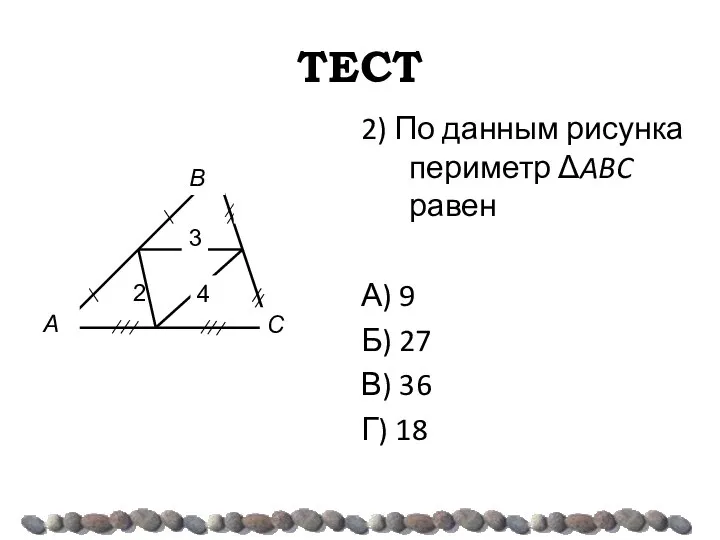
- 44. ТЕСТ 2) По данным рисунка периметр ΔABC равен А) 9 Б) 27 В) 36 Г) 18
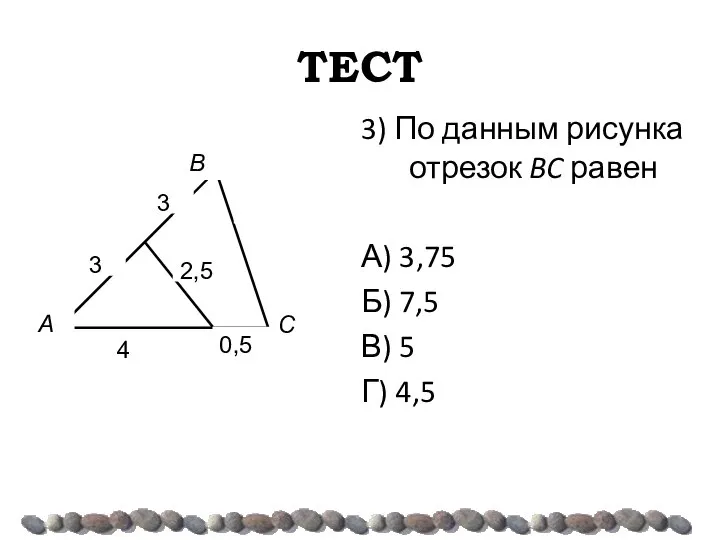
- 45. ТЕСТ 3) По данным рисунка отрезок BC равен А) 3,75 Б) 7,5 В) 5 Г) 4,5
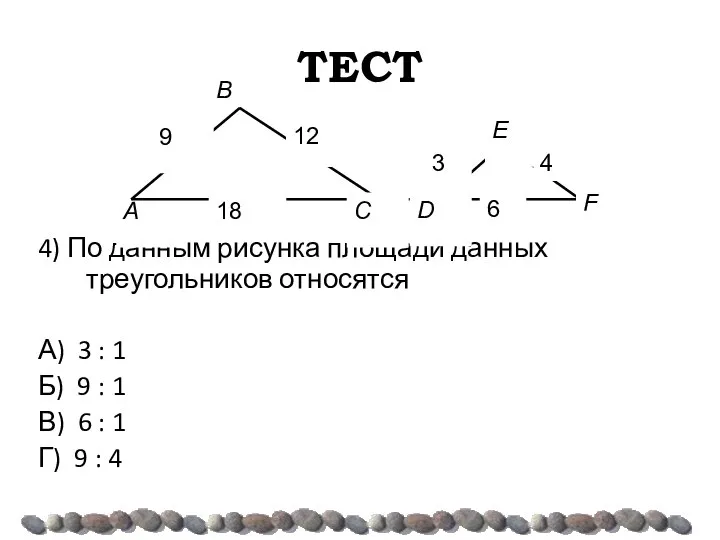
- 46. ТЕСТ 4) По данным рисунка площади данных треугольников относятся А) 3 : 1 Б) 9 :
- 48. Скачать презентацию












 Автор:Аносинская Алина, обучающаяся 4 «А» класса МОУ – СОШ №1. Руководитель:Маркова Ирина Анатольевна
Автор:Аносинская Алина, обучающаяся 4 «А» класса МОУ – СОШ №1. Руководитель:Маркова Ирина Анатольевна  Тригонометрические функции
Тригонометрические функции Осевая симметрия
Осевая симметрия Проценты. 6 класс
Проценты. 6 класс Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Эта многоликая парабола
Эта многоликая парабола Удивительные десятичные дроби. 5 класс
Удивительные десятичные дроби. 5 класс Теорема об отрезках пересекающихся хорд
Теорема об отрезках пересекающихся хорд Аксонометрические проекции
Аксонометрические проекции Модель множественной линейной регрессии
Модель множественной линейной регрессии Основные типы задач по усвоению общего функционального материала
Основные типы задач по усвоению общего функционального материала Смешанные числа
Смешанные числа Числовая окружность
Числовая окружность Мера центральной тенденции. Средние величины и изучение вариации
Мера центральной тенденции. Средние величины и изучение вариации Задачи на железнодорожную тему
Задачи на железнодорожную тему Презентация по математике "Тиждень математики" - скачать
Презентация по математике "Тиждень математики" - скачать  Леонардо по прозвищу Фибоначчи
Леонардо по прозвищу Фибоначчи Урок №3. Полные квадратные уравнения (общая формула) Автор: Ильина Юлия Валерьевна ГБОУ лицей №373 «Экономический лицей»
Урок №3. Полные квадратные уравнения (общая формула) Автор: Ильина Юлия Валерьевна ГБОУ лицей №373 «Экономический лицей»  Вычитание с переходом через десяток
Вычитание с переходом через десяток Понятие корня n – й степени из действительного числа
Понятие корня n – й степени из действительного числа Методы решения уравнений
Методы решения уравнений Измеряем длину окружности Школа № 254 Преподаватель Павлова Марина Константиновна
Измеряем длину окружности Школа № 254 Преподаватель Павлова Марина Константиновна  Ум заключается не только в знании, но и в умении прилагать знание в дело Аристотель
Ум заключается не только в знании, но и в умении прилагать знание в дело Аристотель  Задачи поматематике
Задачи поматематике Графический диктант (зрительный)
Графический диктант (зрительный) Теорема. Площадь трапеции
Теорема. Площадь трапеции Задачи на нахождение остатка . Часть 2
Задачи на нахождение остатка . Часть 2 Путешествие в сказку. Десятичные дроби
Путешествие в сказку. Десятичные дроби