Содержание
- 2. Історичні Відомості Засновники функцій та графіків
- 3. Леонард Ейлер Леона́рд Е́йлер 15 квітня 1707, Базель, Швейцарія — 18 вересня 1783), видатний швейцарський математик
- 4. Джон Непер У ранній молодості, негайно ж після закінчення курсу в Сент-Ендрюського університеті, куди він вступив
- 5. Вільям Отред Отред народився в Ітоні, графство Бекінгемшір (в наші дні - Беркшир), в сім'ї священика.
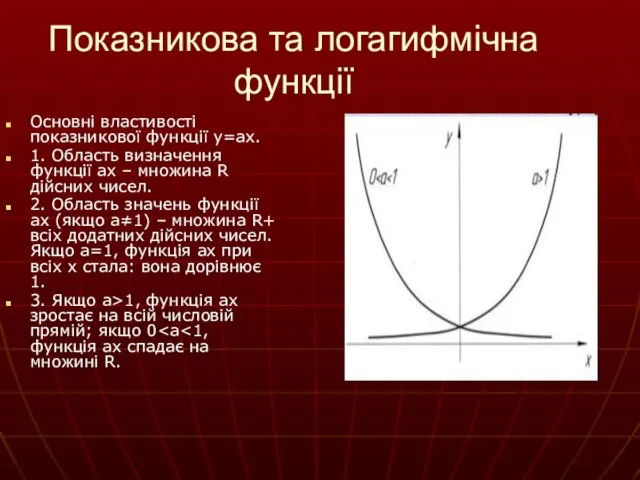
- 6. Показникова та логагифмічна функції Основні властивості показникової функції y=ax. 1. Область визначення функції ax – множина
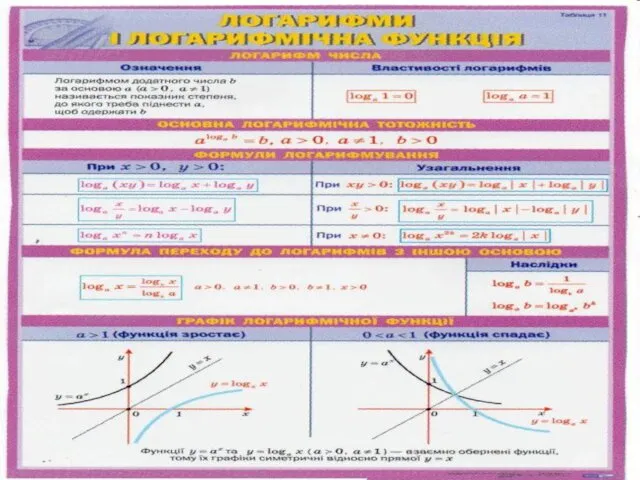
- 7. Основні властивості логарифмічної функції y=logax. 1. Область визначення логарифмічної функції – множина R+ всіх додатних чисел.
- 8. Види рівнянь Розв’язати рівняння 1/4·4x2=8·(0,5)3x Розв'язання 2-2·(22)x2·(2-1)3x; 2-2·22x2=23·2-3x; 2-2+2x2=23-3x; -2+2x2=3-3x; 2x2+3x-5=0; x1=1; x2=-2,5. Відповідь: x1=1; x2=-2,5.
- 9. Функції та їх властивості
- 10. Показникові рівняння та нерівності Метод координат - це спосіб визначення положення точки, фігури або тіла за
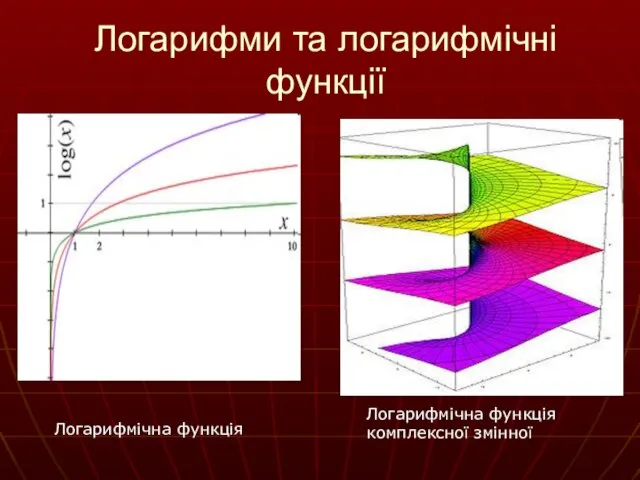
- 11. Логарифми та логарифмічні функції Логарифмічна функція комплексної змінної Логарифмічна функція
- 12. Логарифм – з грецької означає “логос”- відношення і “аритмос”- число. Його винахід пов’язаний з двома постатями:
- 15. Скачать презентацию









 Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Классификация уравнений. (Лекция 3)
Классификация уравнений. (Лекция 3) Степень с целым показателем
Степень с целым показателем Презентация по математике "Конус" - скачать бесплатно
Презентация по математике "Конус" - скачать бесплатно ЕГЭ - 2017. Базовый уровень. Теория делимости
ЕГЭ - 2017. Базовый уровень. Теория делимости Свойства параллельных прямых выполнила учитель математики Твердохлеб Гюнай Эхсановна г.Санкт-Петербург
Свойства параллельных прямых выполнила учитель математики Твердохлеб Гюнай Эхсановна г.Санкт-Петербург  Действия над дробями
Действия над дробями Математика в профессии Слесарь по ремонту строительных машин
Математика в профессии Слесарь по ремонту строительных машин Подготовка к контрольной работе. Многогранники
Подготовка к контрольной работе. Многогранники Три подхода к построению множества целых чисел. (Часть 6)
Три подхода к построению множества целых чисел. (Часть 6) Алгоритм вычисления площади с помощью палетки
Алгоритм вычисления площади с помощью палетки Производные высших порядков. Формула Лейбница. Производные высших порядков. (Семинар 10)
Производные высших порядков. Формула Лейбница. Производные высших порядков. (Семинар 10) Классификация средств измерений
Классификация средств измерений Кусочно-заданные функции
Кусочно-заданные функции Точки и прямые
Точки и прямые Сложение чисел с разными знаками
Сложение чисел с разными знаками Модуль действительного числа. (8 класс)
Модуль действительного числа. (8 класс) Доли. Задачи Г. Остера. Перешеина Н. А.
Доли. Задачи Г. Остера. Перешеина Н. А.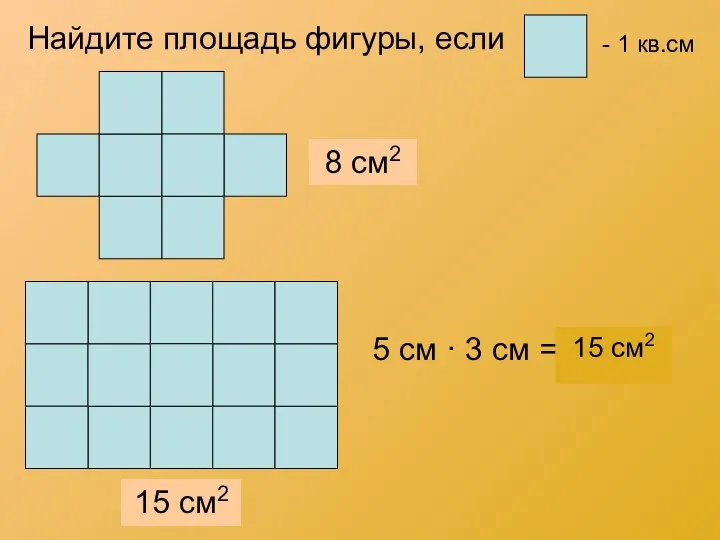 Площадь. Формула площади прямоугольника
Площадь. Формула площади прямоугольника Практическое применение площадей геометрических фигур
Практическое применение площадей геометрических фигур Умножение числа 3 и на 3
Умножение числа 3 и на 3 Командное задание. Численное интегрирование
Командное задание. Численное интегрирование Геометрическая вероятность
Геометрическая вероятность Презентация на тему Прямая и точка Основными геометрическими фигурами на плоскости являются точка и прямая.
Презентация на тему Прямая и точка Основными геометрическими фигурами на плоскости являются точка и прямая.  Графы. Деревья. Таблицы
Графы. Деревья. Таблицы Моделирование при управлении рисками авиапредприятий
Моделирование при управлении рисками авиапредприятий Проценты. Определение
Проценты. Определение Logical expressions
Logical expressions