Понятие производной. Сферы применения производной

Творческое название Гимн производной

Флюксия! Слово прекрасное, может, волшебное?
Флюксия! Петь даже хочется

Цель проекта:

Повторить понятие производной;
Выявить сферы применения производной;
■ Умение самостоятельно находить, изучать

Основополагающий вопрос

Значит
изучать
производную
нам нужно?

Типология проекта:
обобщающий, с элементами
исследования
Категория учащихся:
10 класс
Предметные области:
алгебра и

ПРОБЛЕМНЫЕ ВОПРОСЫ

История возникновения производной.
Задачи, приводящие к применению производной.
Понятие производной.
Геометрический смысл

Мы изучаем производную. А так ли это важно в жизни?

«Дифференциальное

Г. Лейбниц

И. Ньютон 

Р. Декарт

Г.Галилей

Ж. Лагранж

Л. Эйлер

Начнём...

Производная – одно из фундаментальных   понятий математики. Оно возникло в

Термин производная и современные обозначения y’ , f ’ ввёл Ж.Лагранж

А кстати

Большой вклад в изучение дифференциального исчисления внесли  Лопиталь, Бернулли,

САМОПРОВЕРКА!!!

Найдите производные функций.

Формулы:

Примеры применения

САМОПРОВЕРКА!!!

Формулы:

САМОПРОВЕРКА!!!

Производная сложной функции:

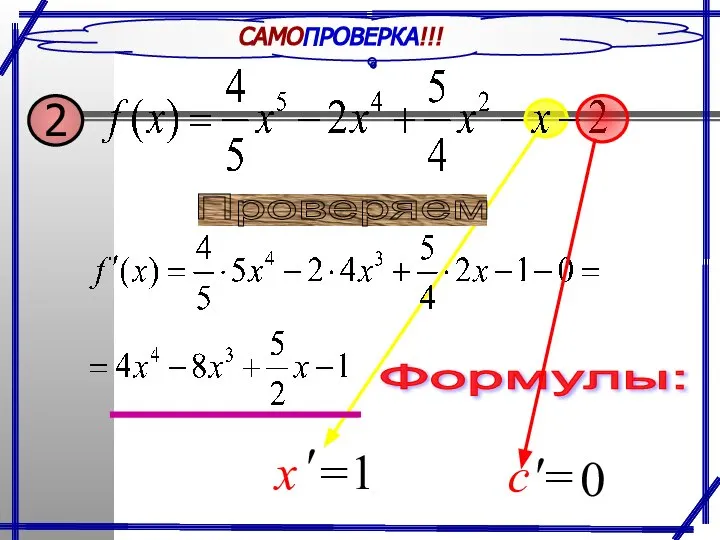
САМОПРОВЕРКА!!!

Проверяем

Производная сложной функции:

ЗНАНИЕ ТЕОРИИ ОБЯЗАТЕЛЬНО!!!

Механический смысл производной

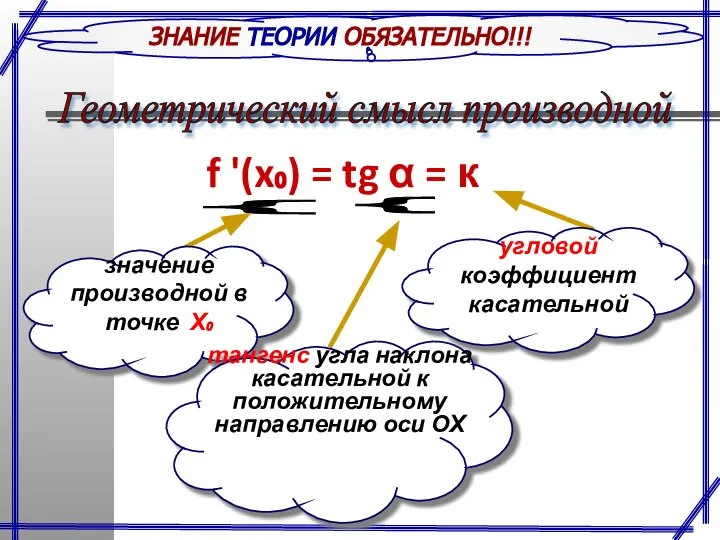
ЗНАНИЕ ТЕОРИИ ОБЯЗАТЕЛЬНО!!!

Геометрический смысл производной

f '(x₀) = tg α =

Производная в математике

«Если продолжить одно из маленьких звеньев ломаной, составляющей кривую линию, то

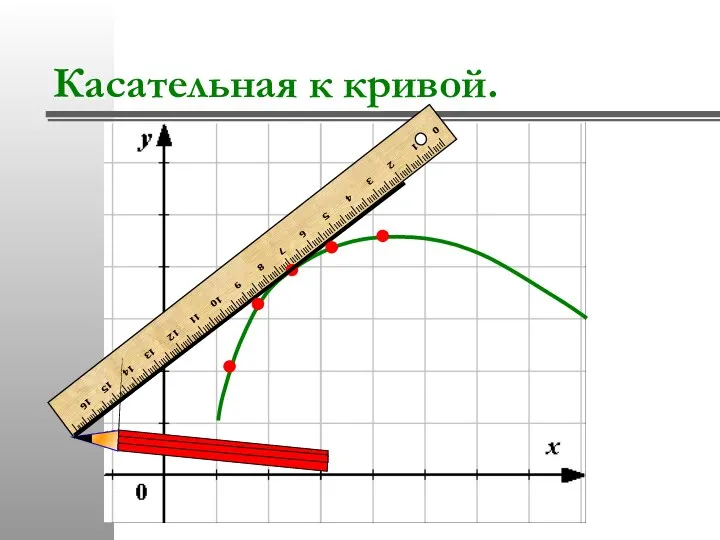
Касательная к кривой.

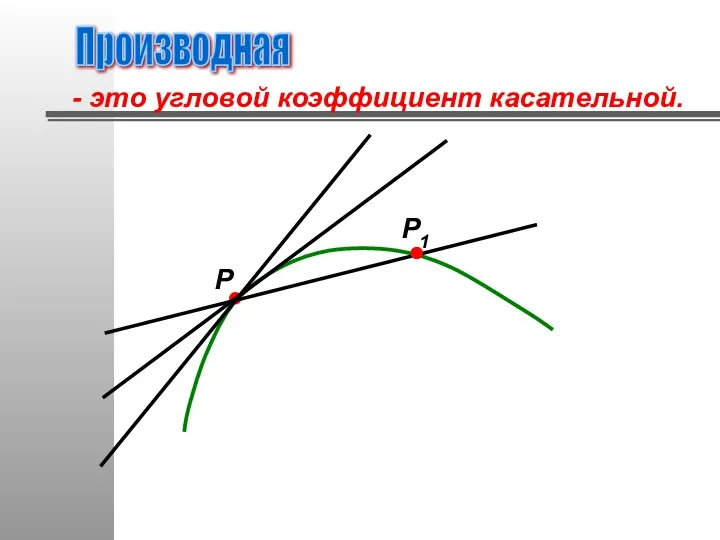
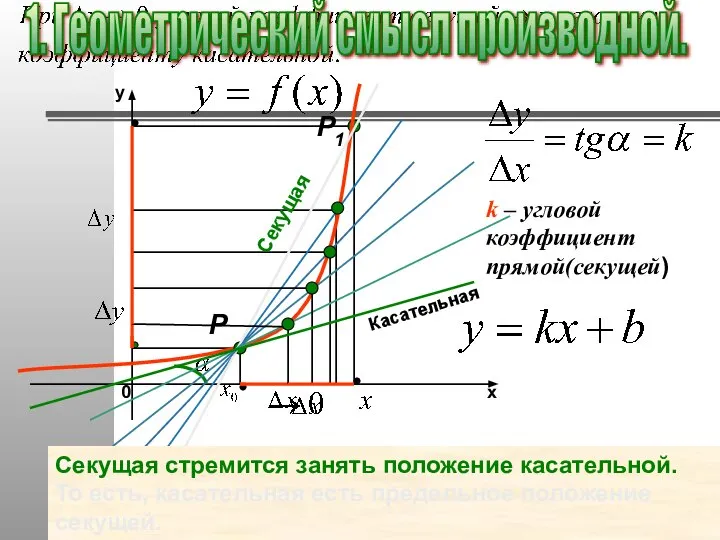
Производная

- это угловой коэффициент касательной.

Р

Р1

k – угловой коэффициент прямой(секущей)

Секущая стремится занять

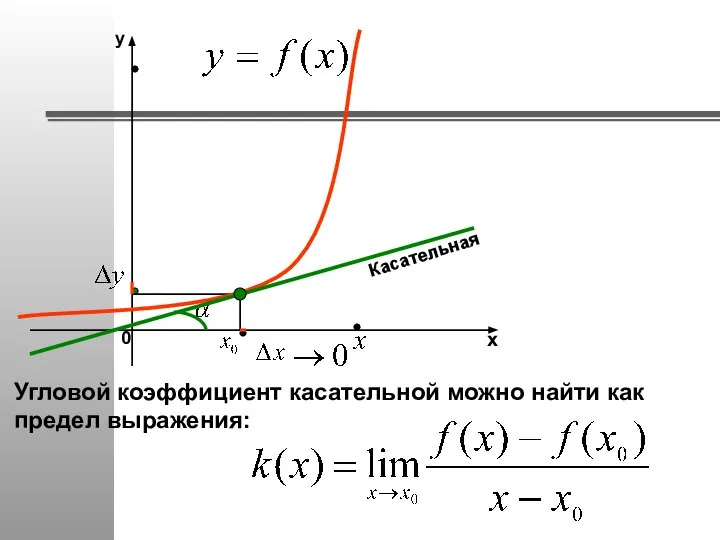
Касательная

Угловой коэффициент касательной можно найти как
предел выражения:

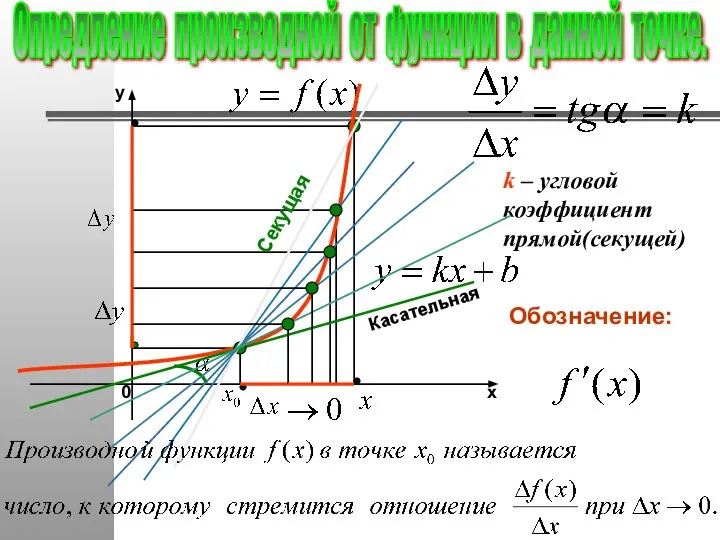
k – угловой коэффициент прямой(секущей)

Касательная

Секущая

Опредление производной от функции

k – угловой коэффициент прямой(касательной)

Касательная

Геометрический смысл производной
Производная

Решение.

f '(x₀) = tg α = к

Угловой коэффициент касательной равен

Производная в физике

Будем вслед за итальянским учёным Г.Галилеем изучать закон свободного падения тел.

Фиксируем момент t, в который мы хотим знать значение скорости v(t).

Задача о теплоёмкости тела

Если температура тела с массой в 1

Задача. Вычислить количество теплоты, которое необходимо для того, чтобы нагреть 1

Решение

Пусть Q=Q(t).
Рассмотрим малый отрезок [t; t+Δt],
на этом отрезке
ΔQ=c(t)

Задача о мгновенной величине тока

Обозначим через q = q(t) количество электричества,

Исаак Ньютон (1643 – 1727)

«Когда величина является максимальной или минимальной,

Используя слово «предел», можно сказать, что мгновенная скорость в точке

.

Δх – перемещение тела

Δt – промежуток времени
в течение которого выполнялось
движение

Механический смысл

Решение.

t = 2,2 (с).

(м/с2) в момент времени t=2 с ?
Решение.

Ускорение равно 8 (м/с2).

Примеры использования в формулах

1) V(t)=X`(t)-скорость
2) а(t)=V`(t)-ускорение
3) I(t)=q`(t)-сила

Производная в химии

Определение производной
Производная – основное
понятие в математике,
характеризующее скорость
изменения функции в
данной точке.

Задача о скорости химической реакции

Средняя скорость растворения соли в воде за

Определение скорости химической реакции.
Скоростью химической
реакции называется
изменение концентрации
реагирующих веществ в
единицу времени.

Зачем нужна производная в реакциях?
Так как скорость химической реакции V

Формула производной в химии.

Если C(t)- закон изменения количества вещества, вступившего

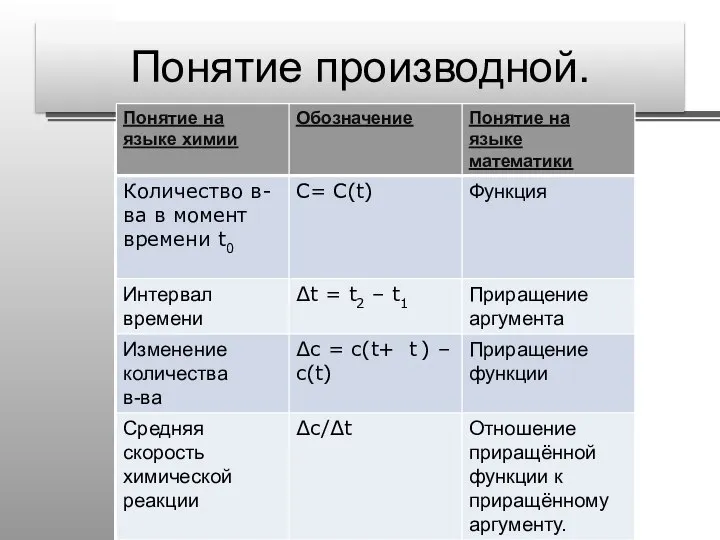
Понятие производной.

Определение скорости реакции.

Предел отношения приращённой функции к приращённому аргументу при

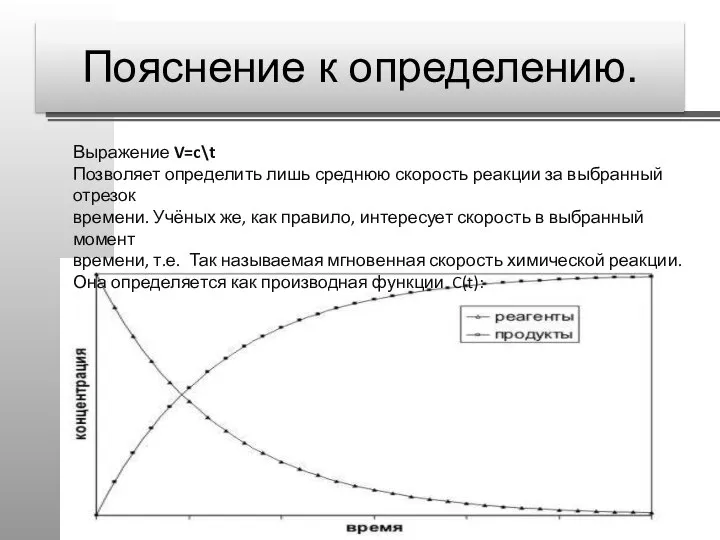
Пояснение к определению.

Выражение V=c\t
Позволяет определить лишь среднюю скорость реакции за

Задача

С системе CO+ Cl2 COCl2 концентрацию СО увеличили от 0,03 до

Решение:
CO+Cl2 COCl2

Vреакции = K1 * Cco * CCl2

K – константа скорости

С

Заключение.
Понятие производной очень важно в химии, особенно при определении скорости

Производная в биологии

Задача :

По известной зависимости численности популяции x (t) определить относительный

Популяция – это совокупность особей данного вида, занимающих определённый участок территории

Решение:

Р = х‘ (t)

Производная в экономике

Экономические задачи

Рассмотрим ситуацию: пусть y - издержки производства, а х -

Аналогичным образом могут быть определены и многие другие экономические величины, имеющие

Экономические задачи

Пусть функция u(t) выражает количество произведенной продукции за время t.

Экономика

Задание.
Оборот предприятия за истекший год описывается через функцию U(t)=0,15t³

Экономика

П (t) = υ' (t) - производительность труда,
где υ (t) -

Производная в географии

Задача :
Вывести формулу для вычисления численности населения на ограниченной

Идея социологической модели Томаса Мальтуса состоит
в том, что прирост населения

Решение:

Пусть у=у(t)- численность населения.
Рассмотрим прирост населения за Δt=t-t0
Δy=kyΔt, где

«…нет ни одной области в математике, которая когда-либо не окажется применимой

Возвращаясь к рассмотренным задачам, важно подчеркнуть следующее:
а) мгновенная скорость неравномерного движения

е) П (t) = υ' (t) - производительность труда, где

ВЫВОД:

Производная нашла широкое применение:
а) в алгебре и

Авторы проекта:

Учёные – химики.

Учёные – математики.

Учёные – биологии.

Учёные – географы.

Учёные – исследователи.

Учёные – физики.