Содержание
- 2. Исторические сведения. Происхождение понятия производной. Ряд задач дифференциального исчисления был решён ещё в древности. Основное понятие
- 3. Для доказательства своего правила Ньютон, следуя в основном Ферма, рассматривает бесконечно малое приращение времени dt, которое
- 4. Путь к производной через касательную кривой. Математиков XV – XVII вв. долго волновал вопрос о нахождении
- 5. С самого начала XVII в. немало учёных, в том числе Торричелли, Вивиани, Роберваль, Барроу, пыталось найти
- 6. Основываясь на результатах Ферма и некоторых других выводах, Лейбниц значительно полнее своих предшественников решил задачу, о
- 7. Можно привести и другие примеры, показывающие, какую большую роль играет понятие производной в науке и технике.
- 8. Символы и термины. Приращение абсциссы Лейбниц обозначал через dx, соответствующее приращение ординаты – через dy. Ныне
- 9. Обозначения y ' и f ' (x) для производной ввёл Лагранж. Сам термин «производная» впервые встречается
- 10. Со времён Коши, впервые ясно определившего производную как предел отношения приращения функции ∆ y к приращению
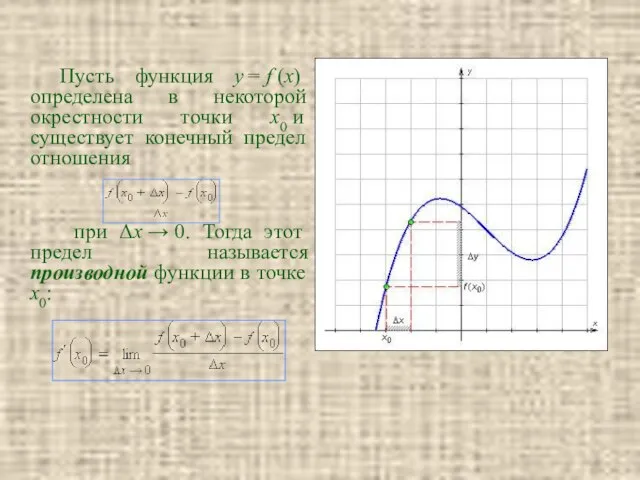
- 11. Пусть функция y = f (x) определена в некоторой окрестности точки x0 и существует конечный предел
- 13. С физической точки зрения этот предел есть значение скорости изменения функции f(x) относительно ее аргумента при
- 16. Скачать презентацию












 Интегрированный урок «Математика в экологии» 5 класс тема «Числовые выражения» Учитель математики МОУ СОШ №10 с УИОП Умарова
Интегрированный урок «Математика в экологии» 5 класс тема «Числовые выражения» Учитель математики МОУ СОШ №10 с УИОП Умарова  Математические основы анализа свойств систем и наблюдения их состояния (лекция № 17)
Математические основы анализа свойств систем и наблюдения их состояния (лекция № 17) Магические квадраты
Магические квадраты Сложение и умножение неравенств
Сложение и умножение неравенств Внеклассное мероприятие по математике
Внеклассное мероприятие по математике Линейные уравнения. 7 класс
Линейные уравнения. 7 класс Метод главных элементов для решения системы линейных уравнений
Метод главных элементов для решения системы линейных уравнений Среднее арифметическое. 5 класс, урок 133
Среднее арифметическое. 5 класс, урок 133 Отношение величин математика 6 класс Учитель математики МОУ «Лицей №6» г.Воскресенск Павлова Наталья Валерьевна
Отношение величин математика 6 класс Учитель математики МОУ «Лицей №6» г.Воскресенск Павлова Наталья Валерьевна  Свойства функции
Свойства функции Презентация по математике "Считаем до 10" - скачать бесплатно
Презентация по математике "Считаем до 10" - скачать бесплатно Тригонометрические уравнения
Тригонометрические уравнения Перевірка наявності зв'язку між змінними
Перевірка наявності зв'язку між змінними Переміщення та його властивості
Переміщення та його властивості Задача на кратчайший путь
Задача на кратчайший путь Математические методы в педагогике
Математические методы в педагогике 14 марта - Международный день числа Пи (International Day)
14 марта - Международный день числа Пи (International Day) Симметрия. Ось симметрии
Симметрия. Ось симметрии Параллельные прямые
Параллельные прямые Матриці та дії над ними
Матриці та дії над ними Последовательность расчет при прямых измерениях
Последовательность расчет при прямых измерениях Научно – исследовательский проект ученицы 9 «Б» класса, Саночкиной Екатерины
Научно – исследовательский проект ученицы 9 «Б» класса, Саночкиной Екатерины  Графический способ решения уравнений. Урок 95
Графический способ решения уравнений. Урок 95 Аттестационная работа. Образовательная программа курса по математике «Методы решения уравнений, неравенств и их систем»
Аттестационная работа. Образовательная программа курса по математике «Методы решения уравнений, неравенств и их систем» Решение задач на совместную работу при подготовке учащихся 9-х классов к ГИА
Решение задач на совместную работу при подготовке учащихся 9-х классов к ГИА Тригонометрические функции (11 класс)
Тригонометрические функции (11 класс) Элементы комбинаторики (обобщающий урок). 9 класс
Элементы комбинаторики (обобщающий урок). 9 класс Комбинаторика. Свойства сочетаний. (Лекция 11)
Комбинаторика. Свойства сочетаний. (Лекция 11)