Содержание
- 2. Первые теоретические сведения, связанные с прогрессиями, дошли до нас в документах Древней Греции. В Древнем Египте
- 3. Примеры отдельных арифметических и геометрических прогрессий можно встретить еще в древневавилонских и греческих надписях, имеющих возраст
- 4. В клинописных табличках вавилонян, как и в египетских папирусах, относящихся ко второму тысячелетию до нашей эры,
- 5. Как Архимед вычислял площадь круга… Вначале Архимед вписывал в круг шестиугольник, затем на каждой стороне построил
- 6. В ходе своих исследований Архимед нашел сумму бесконечной геометрической прогрессии со знаменателем 1/4, что явилось первым
- 7. В “Исчислении песчинок” Архимед впервые сопоставляет арифметическую и геометрическую прогрессии, устанавливает между ними связь: 1, 2,
- 8. Одно из доказательств Архимеда, изложенное в его произведении “Квадратура параболы”, сводится к суммированию бесконечно убывающей геометрической
- 9. Пифагор и последовательности Пифагор (IV в. до н. э.) и его ученики рассматривали последовательности, связанные с
- 10. В древности вычислители часто считали с помощью камешков и, естественно, отмечали случаи, когда камешки можно было
- 11. Зададим эту последовательностей формулой п-ого члена. Последовательность (ап) треугольных чисел получается из последовательности натуральных чисел 1,
- 12. Последовательность (bп) квадратных чисел аналогичным способом получается из последовательности нечетных чисел 1, 3, 5, ... ,
- 13. Последовательность (cп) пятиугольных чисел аналогичным способом получается из последовательности нечетных чисел 1, 4, 7, ... ,
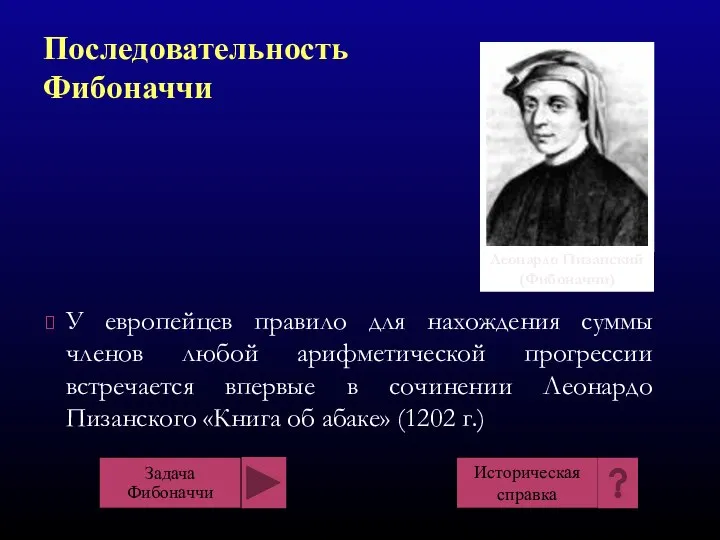
- 14. У европейцев правило для нахождения суммы членов любой арифметической прогрессии встречается впервые в сочинении Леонардо Пизанского
- 15. "Книге абака" представляет собой объемный труд, содержащий почти все арифметические и алгебраические сведения того времени и
- 16. Наиболее известной из сформулированных Фибоначчи задач является "задача о размножении кроликов", которая привела к открытию числовой
- 17. Задача Фибоначчи : Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы
- 18. Ясно, что если считать первую пару кроликов новорожденными, то на второй месяц мы будем по прежнему
- 19. Чтобы ответить на вопрос задачи, воспользуемся следующей схемой. Кружочек — это пара кроликов. Стрелка, направленная вниз,
- 20. «Сколько пар кроликов в один год от одной пары родится». Ряд чисел 0, 1, 1, 2,
- 21. Таким образом, если обозначить число пар кроликов, имеющихся на n- м месяце через Uk , то
- 22. Числа un, образующие последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,
- 23. Сведения из истории Сами по себе прогрессии известны так давно, что конечно, нельзя говорить о том,
- 24. В Германии молодой Карл Гаусс (1777-1855) нашел моментально сумму всех натуральных чисел от 1 до 100,
- 25. Общая формула для вычисления суммы любой бесконечно убывающей геометрической прогрессии была выведена в первой половине XVII
- 26. На связь между прогрессиями первым обратил внимание великий Архимед. В печати же эти мысли отчетливо прозвучали
- 27. В начале XIII века в городе Пизе (Италия) жил большой знаток всевозможных соотношений между числами и
- 28. Одна из задач, рассмотренная Фибоначчи, называется "задачей о поиске наилучшей системы гирь для взвешивания на рычажных
- 29. Сущность "задачи Баше-Менделеева" состоит в следующем: при какой системе гирь, имея их по одной, можно взвесить
- 30. Еще одна задача интересна в исторической связи и носит имя "задачи о семи старухах". Старухи направляются
- 31. Общее число всего перечисленного 7+49+343+2401+16807+117649=137256 1 7 6 5 4 3 2 У каждой старухи 7
- 32. Другой способ решения задачи 7, 49, 343, 2401, 16807, 117649 –это геометрическая прогрессия, первый член b1=
- 33. Искусство Леонардо в решении числовых задач изумляло всех. Высокая репутация Фибоначчи привлекла однажды (в 1225 г.)
- 34. В XIX веке в Пизе был поставлен памятник учёному
- 36. Скачать презентацию
































 Лекция 08. Однородные координаты
Лекция 08. Однородные координаты Среднее арифметическое чисел
Среднее арифметическое чисел Простейшие задачи в координатах
Простейшие задачи в координатах Теория вероятности.Операции над событиями
Теория вероятности.Операции над событиями Задания по математике для учеников 1 класса
Задания по математике для учеников 1 класса Решение логической задачи (1 класс)
Решение логической задачи (1 класс) Урок математики во 2 классе (УМК «Гармония») по теме «Единицы времени. Час. Минута. Секунда». Разработала учитель начальн
Урок математики во 2 классе (УМК «Гармония») по теме «Единицы времени. Час. Минута. Секунда». Разработала учитель начальн Аттестационная работа. Рабочая программа по внеурочной деятельности «Страна геометрия»
Аттестационная работа. Рабочая программа по внеурочной деятельности «Страна геометрия» Шкалы и координаты (5 класс) - Презентация по математике_
Шкалы и координаты (5 класс) - Презентация по математике_ Место данного урока в общей системе уроков по математике: Многочлены
Место данного урока в общей системе уроков по математике: Многочлены Бесконечно убывающая геометрическая прогрессия. 10 класс
Бесконечно убывающая геометрическая прогрессия. 10 класс «Математика и здоровье» Подготовила: Учитель математики МОУ гимназии №88 Якунина Любовь Анатольевна
«Математика и здоровье» Подготовила: Учитель математики МОУ гимназии №88 Якунина Любовь Анатольевна  Разложение на множители с помощью группировки
Разложение на множители с помощью группировки Функция y=sinx
Функция y=sinx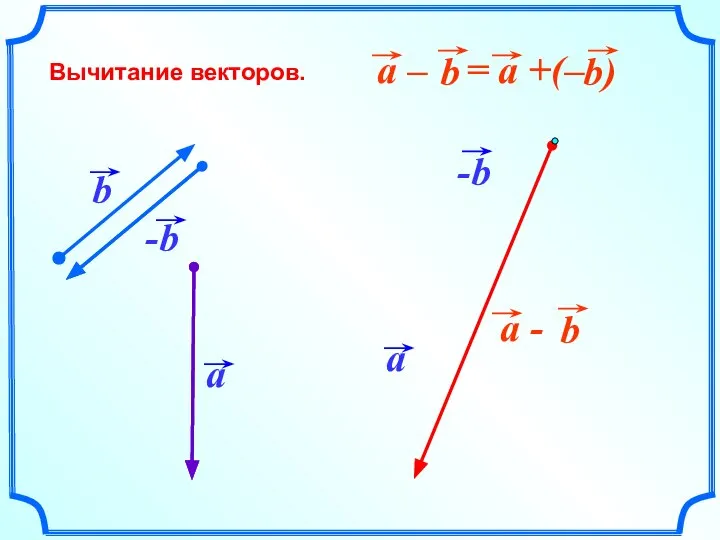 Вычитание и сложение векторов. Правило параллелограмма
Вычитание и сложение векторов. Правило параллелограмма Презентация по математике "Решение уравнений с опорой на отношение «части и целое»" - скачать
Презентация по математике "Решение уравнений с опорой на отношение «части и целое»" - скачать  У Р А В Н Е Н И Е Урок математики, 5 класс. Учитель математики: Ожеред Сергей Тимофеевич МОУ-СОШ с.Батурино Асиновского р-на
У Р А В Н Е Н И Е Урок математики, 5 класс. Учитель математики: Ожеред Сергей Тимофеевич МОУ-СОШ с.Батурино Асиновского р-на  Решение логических задач табличным способом
Решение логических задач табличным способом Элементы статистики
Элементы статистики Деление на десятичную дробь
Деление на десятичную дробь Математический КВН
Математический КВН Статистические методы изучения взаимосвязи социально-экономических явлений
Статистические методы изучения взаимосвязи социально-экономических явлений Измерение углов
Измерение углов Выборочное наблюдение
Выборочное наблюдение Элементы статистической обработки данных. 7 класс
Элементы статистической обработки данных. 7 класс Простейшие показательные уравнения
Простейшие показательные уравнения Математика в профессии
Математика в профессии Решение задач. Параллельные прямые
Решение задач. Параллельные прямые