Содержание
- 2. Позиционными задачами называют такие, в которых определяется взаимное расположение геометрических фигур в пространстве Существует три типа
- 3. Взаимное пересечение геометрических фигур Две геометрические фигуры, пересекаясь, дают общий элемент: Прямая с прямой - точку
- 4. Из всего многообразия этих задач выделяются две общие задачи, которые называют главными позиционными задачами: Первая главная
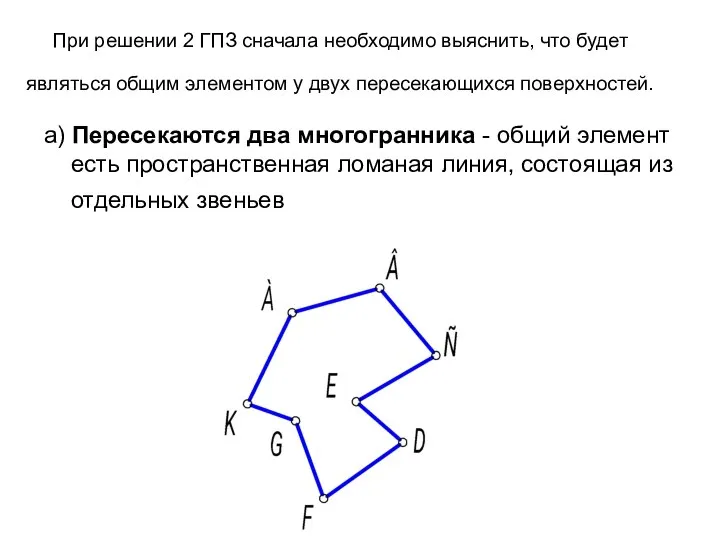
- 5. При решении 2 ГПЗ сначала необходимо выяснить, что будет являться общим элементом у двух пересекающихся поверхностей.
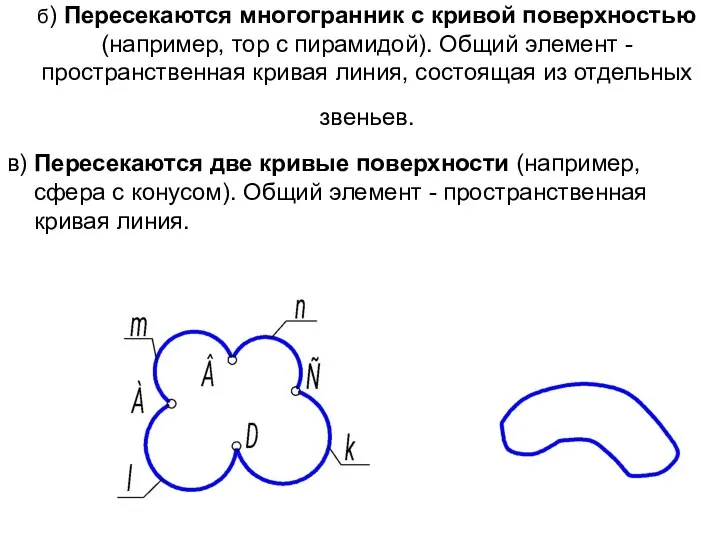
- 6. б) Пересекаются многогранник с кривой поверхностью (например, тор с пирамидой). Общий элемент - пространственная кривая линия,
- 7. Далее необходимо определить количество общих элементов пересекающихся поверхностей. Определяется оно в зависимости от характера пересечения поверхностей.
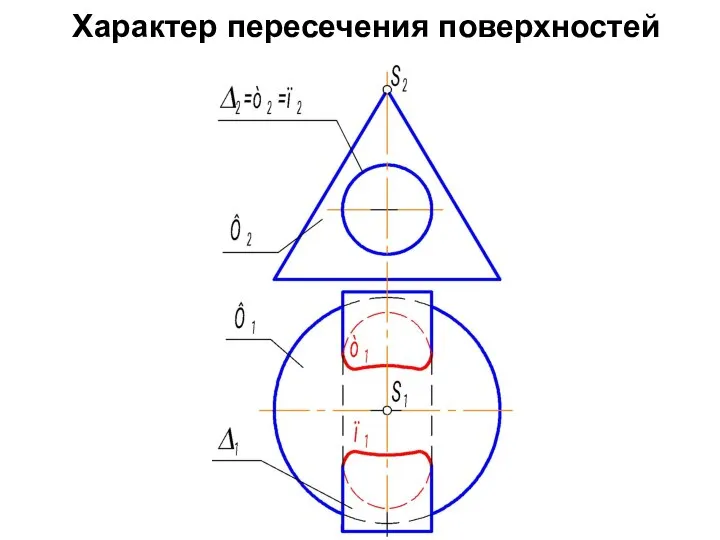
- 8. Характер пересечения поверхностей
- 9. Такой характер пересечения, когда одна из поверхностей насквозь пронзает другую, называется чистое проницание. В этом случае
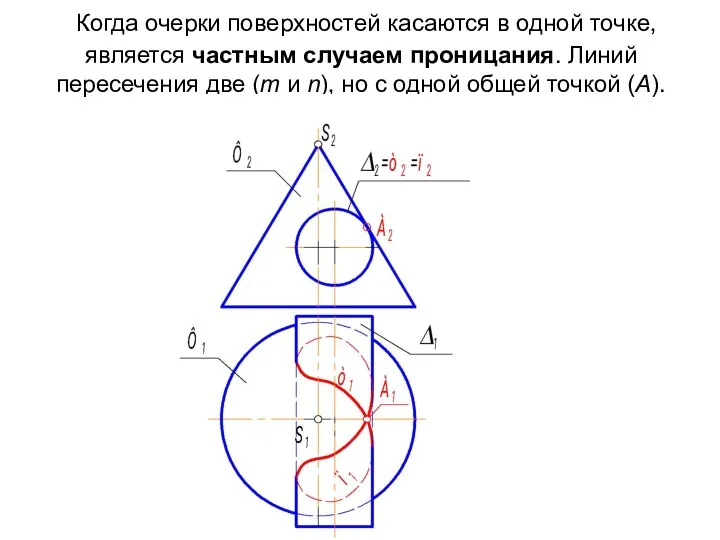
- 10. Когда очерки поверхностей касаются в одной точке, является частным случаем проницания. Линий пересечения две (m и
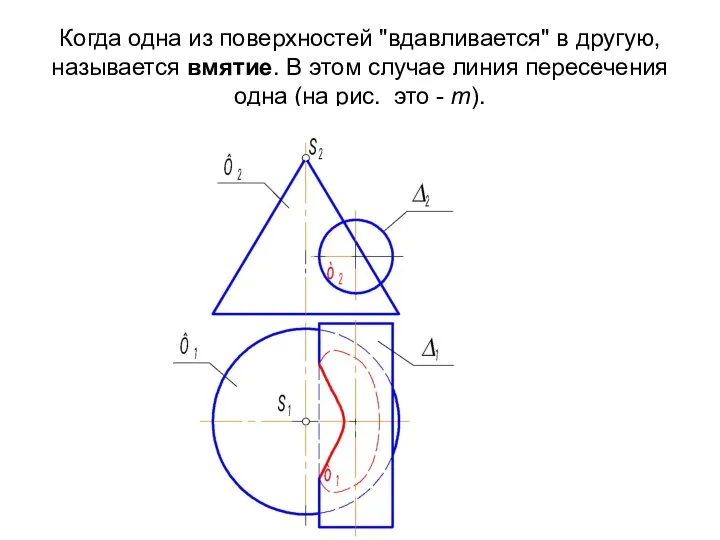
- 11. Когда одна из поверхностей "вдавливается" в другую, называется вмятие. В этом случае линия пересечения одна (на
- 12. Решение главных позиционных задач. 3 случая. 3 алгоритма. Здесь имеет место З случая: обе пересекающиеся фигуры
- 13. Фигуры могут занимать проецирующее положение. Таковыми являются: прямая, плоскость, а из всех известных нам поверхностей проецирующее
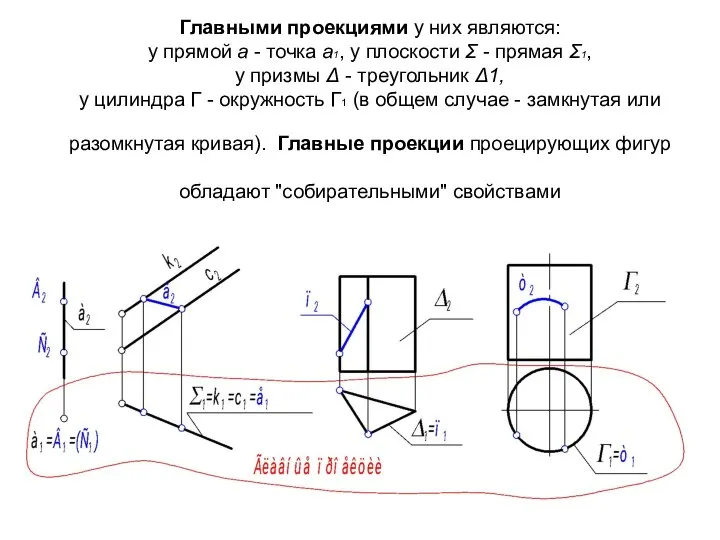
- 14. Главными проекциями у них являются: у прямой а - точка а1, у плоскости Σ - прямая
- 15. Решение задач в случае, когда обе пересекающиеся фигуры занимают проецирующее положение. 1 алгоритм Задача : Найти
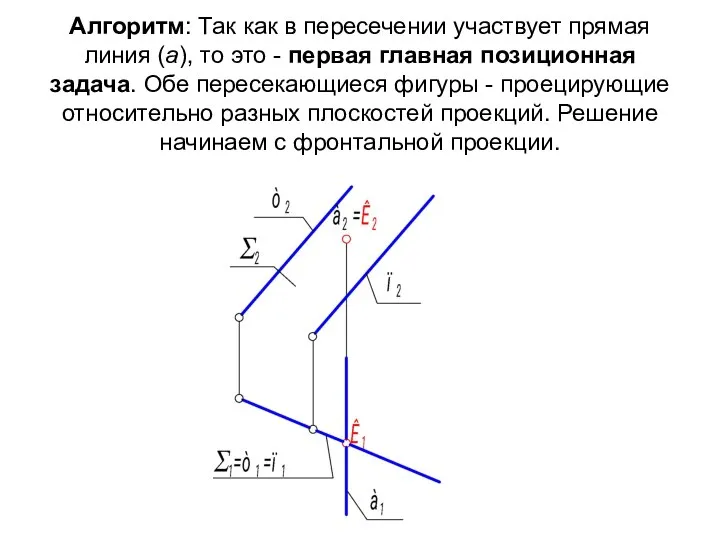
- 16. Алгоритм: Так как в пересечении участвует прямая линия (а), то это - первая главная позиционная задача.
- 17. Выполним краткую алгоритмическую запись вышеизложенного: Σ(m || n) ∩ а = К; 1 ГПЗ, 1 алгоритм.
- 18. Таким образом, решение 1 ГПЗ по первому алгоритму заключается в следующем: Проекции общего элемента на чертеже
- 19. Вторую главную позиционную задачу решим в соответствии с рассмотренным алгоритмом. Задача: найти проекции линии пересечения горизонтально
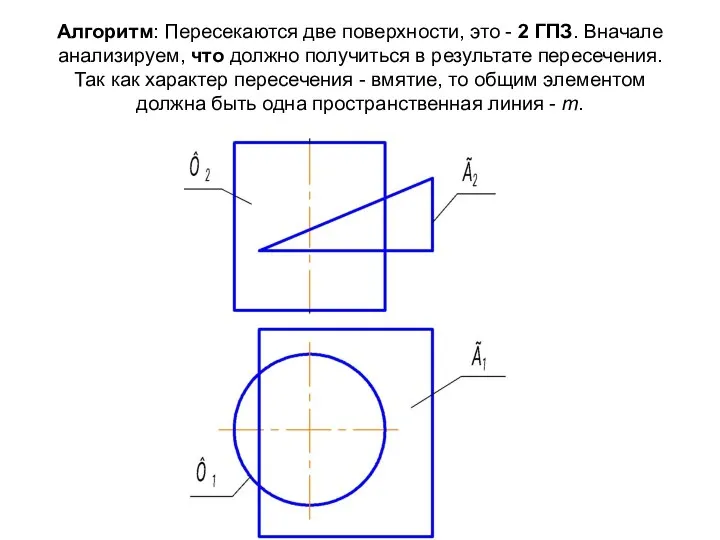
- 20. Алгоритм: Пересекаются две поверхности, это - 2 ГПЗ. Вначале анализируем, что должно получиться в результате пересечения.
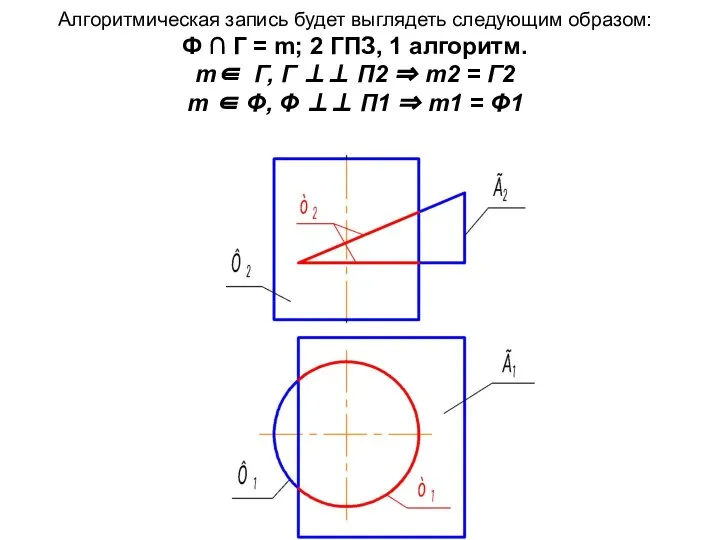
- 21. Алгоритмическая запись будет выглядеть следующим образом: Ф ∩ Г = m; 2 ГПЗ, 1 алгоритм. m∈
- 22. Проанализируем, из чего состоит линия пересечения m. Как мы уже предполагали, это пространственная линия. Она состоит
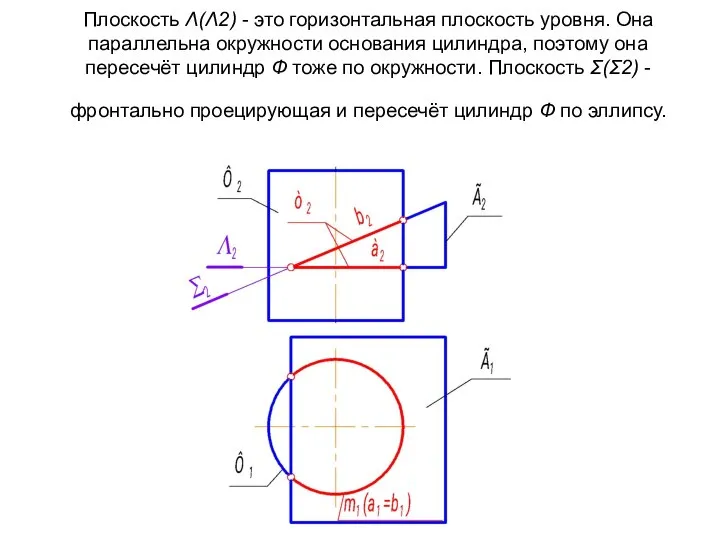
- 23. Плоскость Λ(Λ2) - это горизонтальная плоскость уровня. Она параллельна окружности основания цилиндра, поэтому она пересечёт цилиндр
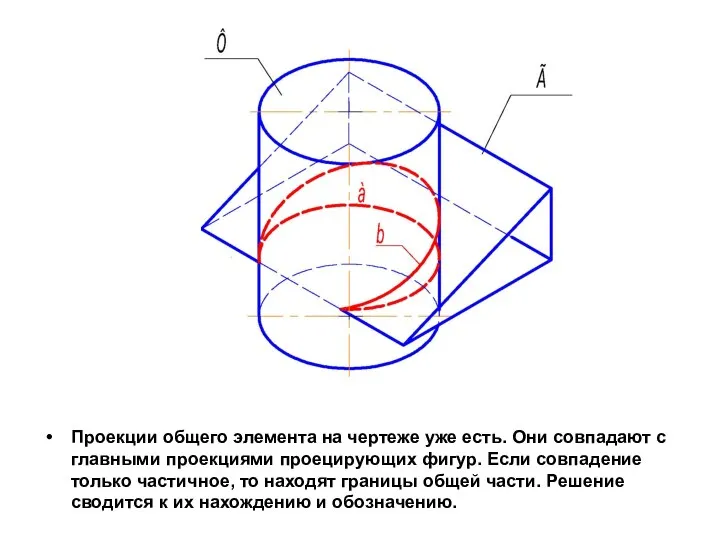
- 24. Проекции общего элемента на чертеже уже есть. Они совпадают с главными проекциями проецирующих фигур. Если совпадение
- 25. Решение задач в случае, когда одна из пересекающихся фигур проецирующая, вторая - непроецирующая. 2 алгоритм
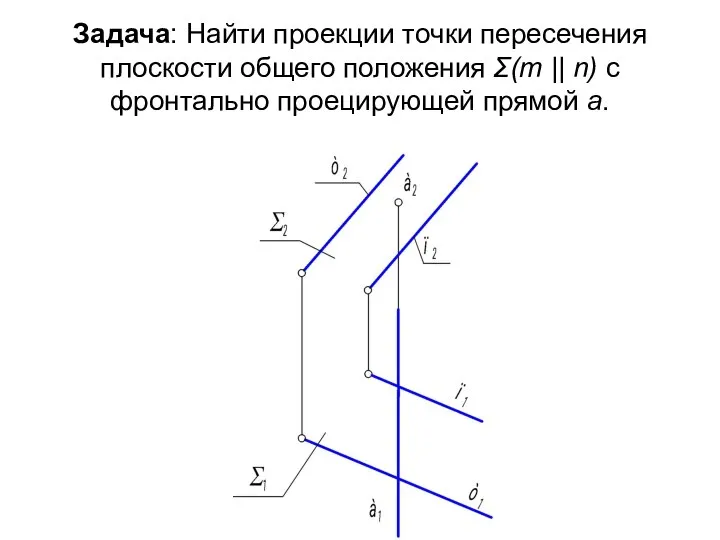
- 26. Задача: Найти проекции точки пересечения плоскости общего положения Σ(m || n) с фронтально проецирующей прямой а.
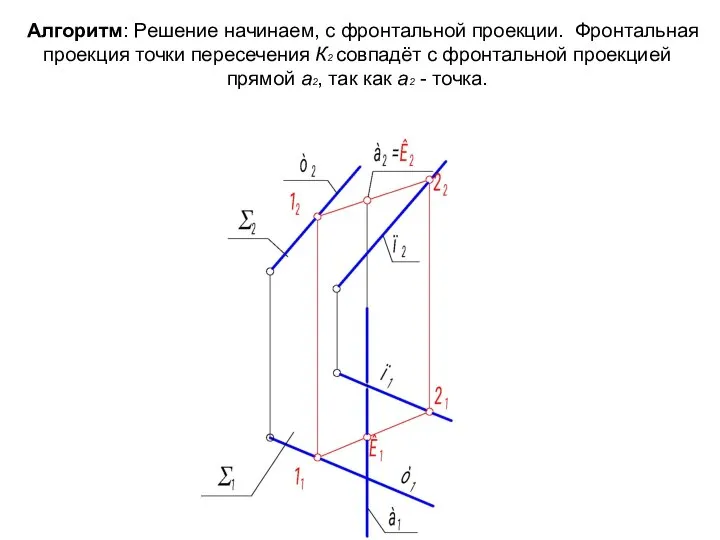
- 27. Алгоритм: Решение начинаем, с фронтальной проекции. Фронтальная проекция точки пересечения К2 совпадёт с фронтальной проекцией прямой
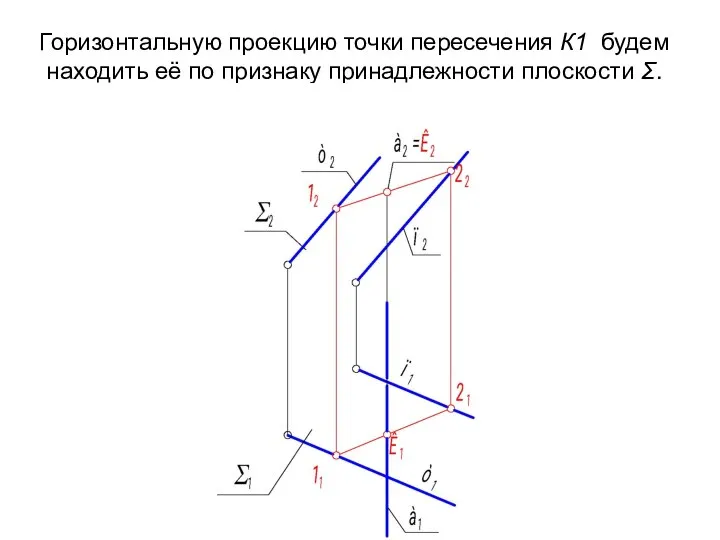
- 28. Горизонтальную проекцию точки пересечения К1 будем находить её по признаку принадлежности плоскости Σ.
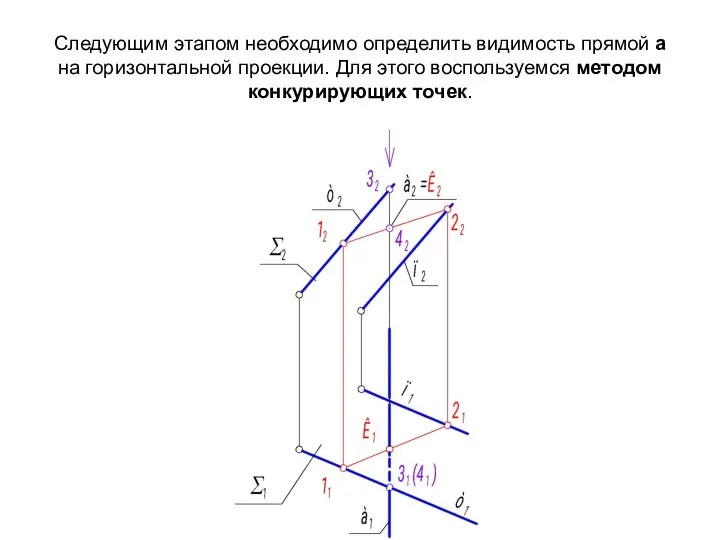
- 29. Следующим этапом необходимо определить видимость прямой а на горизонтальной проекции. Для этого воспользуемся методом конкурирующих точек.
- 30. Выполним краткую алгоритмическую запись решения: Σ(m || n) ∩ a = K; 1 ГПЗ, 2 алгоритм
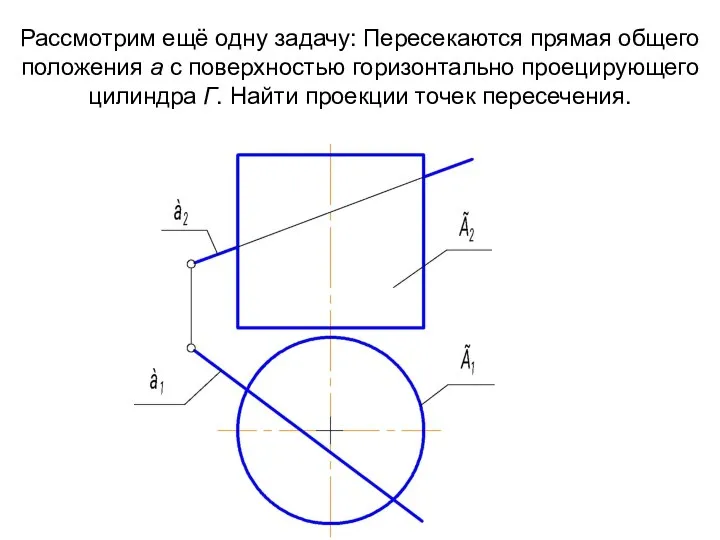
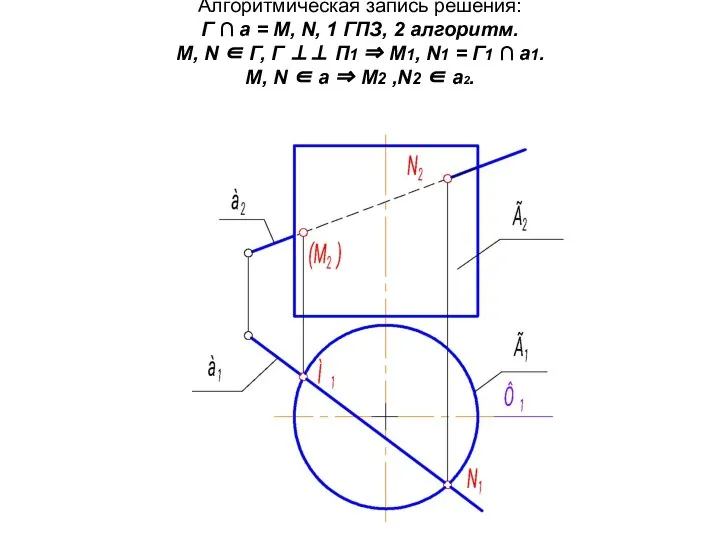
- 31. Рассмотрим ещё одну задачу: Пересекаются прямая общего положения а с поверхностью горизонтально проецирующего цилиндра Г. Найти
- 32. Алгоритмическая запись решения: Г ∩ а = М, N, 1 ГПЗ, 2 алгоритм. М, N ∈
- 33. Решение задач по 2 алгоритму сводится к следующему: Выделяют из двух заданных фигур проецирующую и отмечают
- 34. Решение 2 ГПЗ по 2 алгоритму рассмотрим на примере конических сечений. При пересечении конуса различными плоскостями
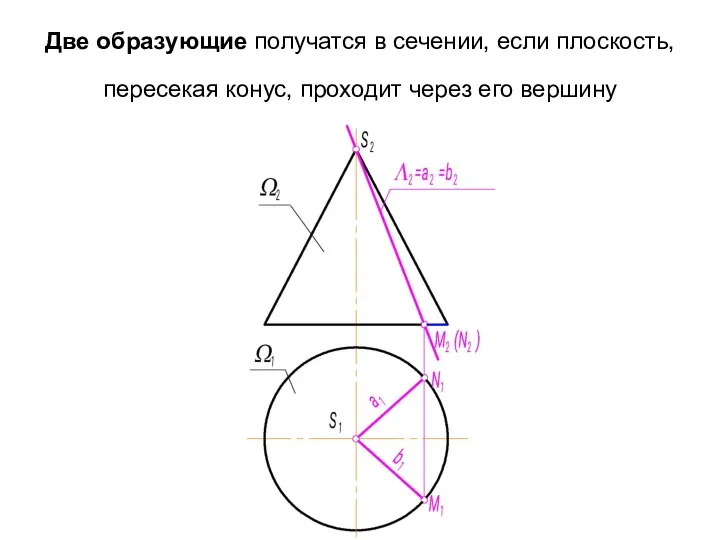
- 35. Две образующие получатся в сечении, если плоскость, пересекая конус, проходит через его вершину
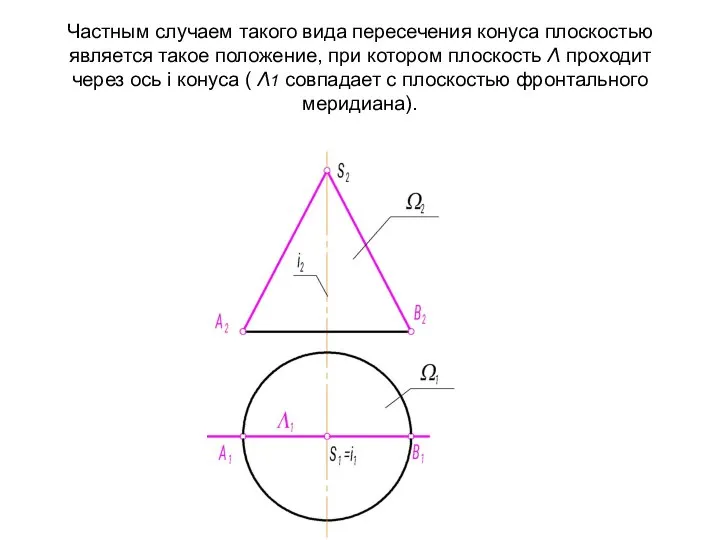
- 36. Частным случаем такого вида пересечения конуса плоскостью является такое положение, при котором плоскость Λ проходит через
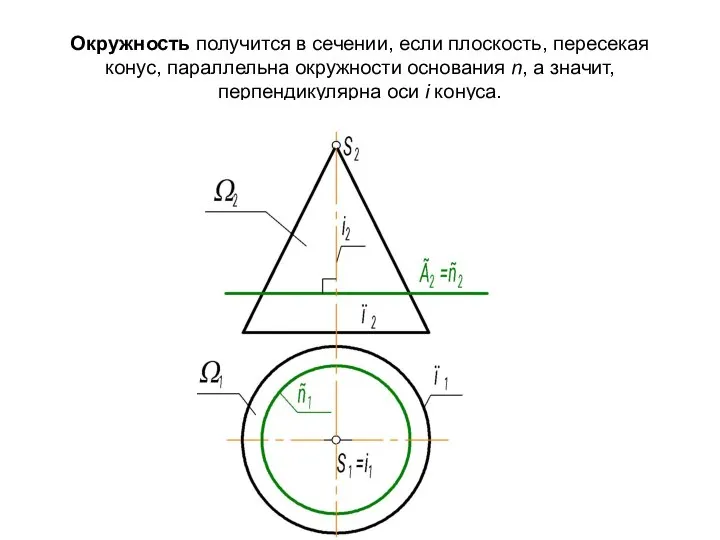
- 37. Окружность получится в сечении, если плоскость, пересекая конус, параллельна окружности основания n, а значит, перпендикулярна оси
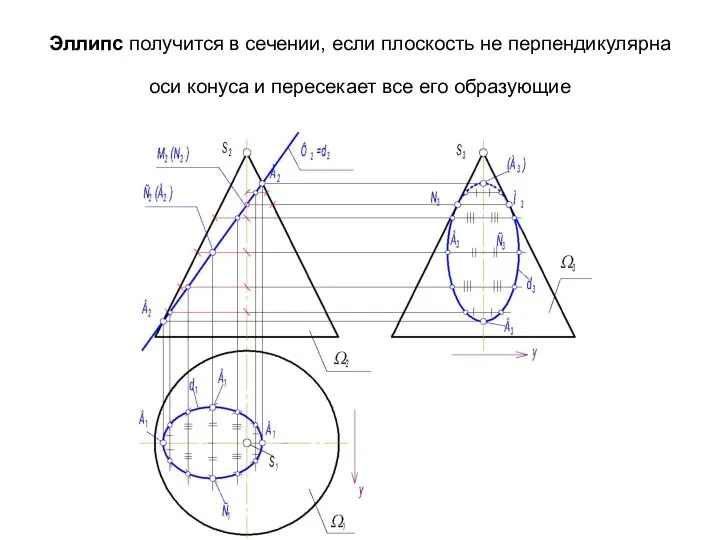
- 38. Эллипс получится в сечении, если плоскость не перпендикулярна оси конуса и пересекает все его образующие
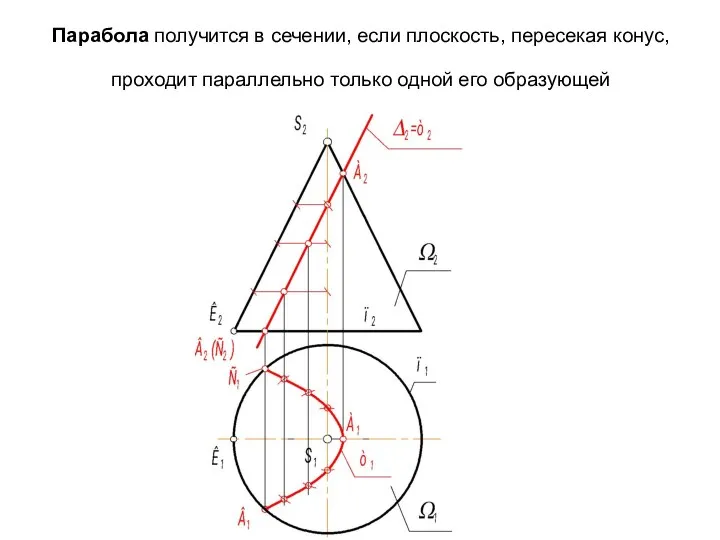
- 39. Парабола получится в сечении, если плоскость, пересекая конус, проходит параллельно только одной его образующей
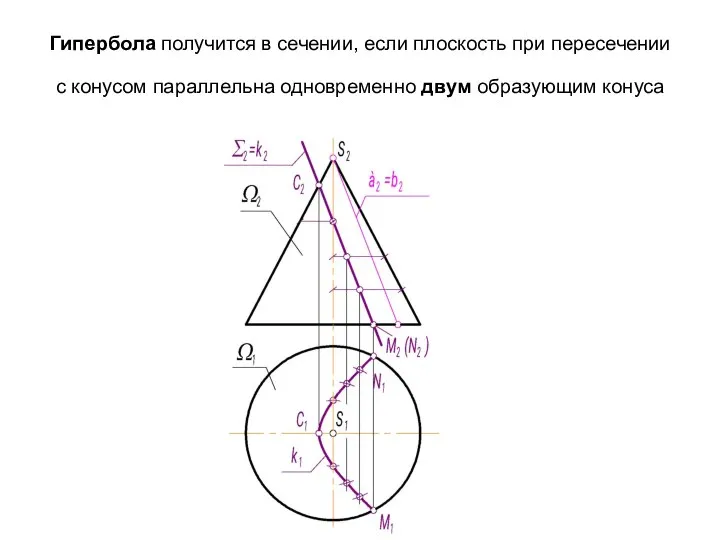
- 40. Гипербола получится в сечении, если плоскость при пересечении с конусом параллельна одновременно двум образующим конуса
- 41. Рассмотрим ещё одну задачу на пересечение поверхностей, из которых одна проецирующая, вторая - непроецирующая. Задача: Построить
- 42. Алгоритм: 2 ГПЗ, 2 алг. Алгоритм: 2 ГПЗ, 2 алг. 1. Вначале определяем, что должно получиться
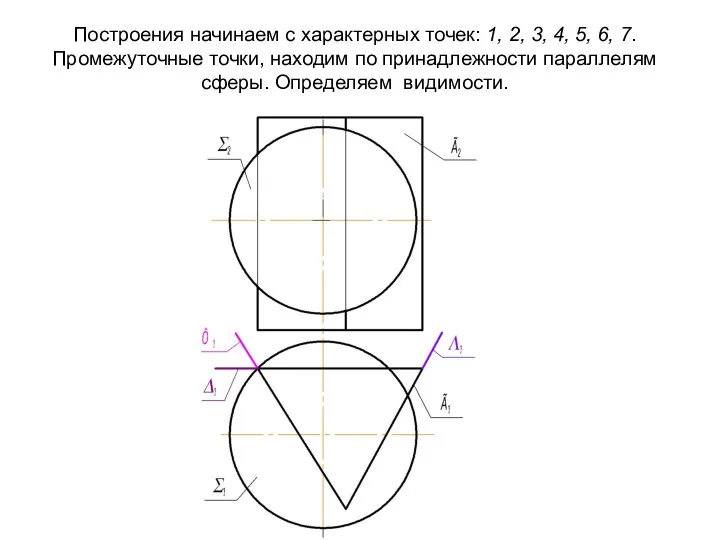
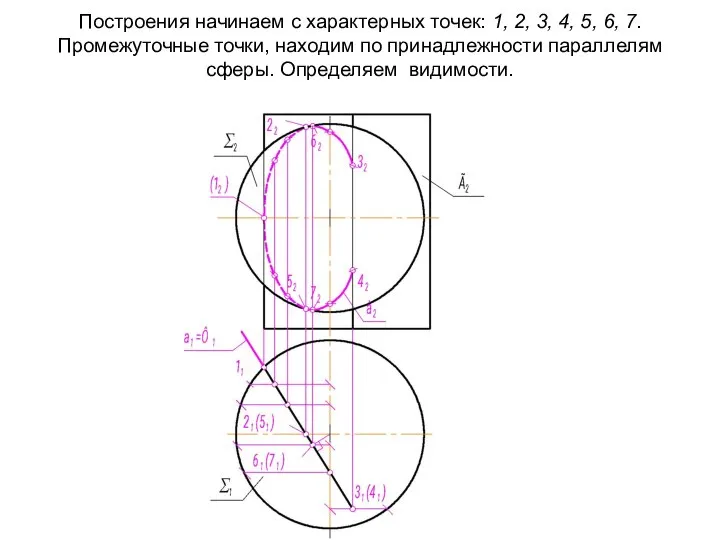
- 43. Построения начинаем с характерных точек: 1, 2, 3, 4, 5, 6, 7. Промежуточные точки, находим по
- 44. Построения начинаем с характерных точек: 1, 2, 3, 4, 5, 6, 7. Промежуточные точки, находим по
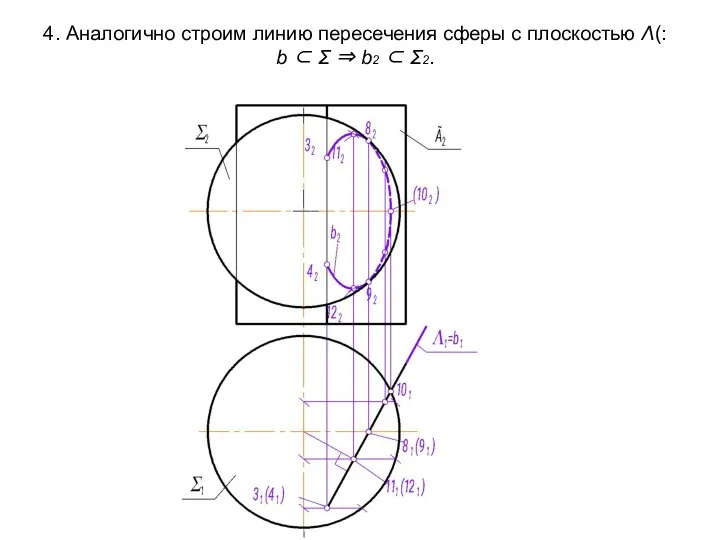
- 45. 4. Аналогично строим линию пересечения сферы с плоскостью Λ(: b ⊂ Σ ⇒ b2 ⊂ Σ2.
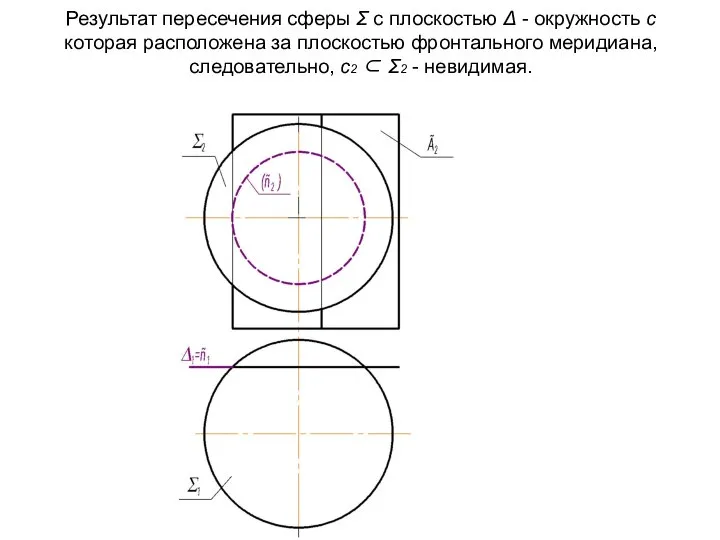
- 46. Результат пересечения сферы Σ с плоскостью Δ - окружность с которая расположена за плоскостью фронтального меридиана,
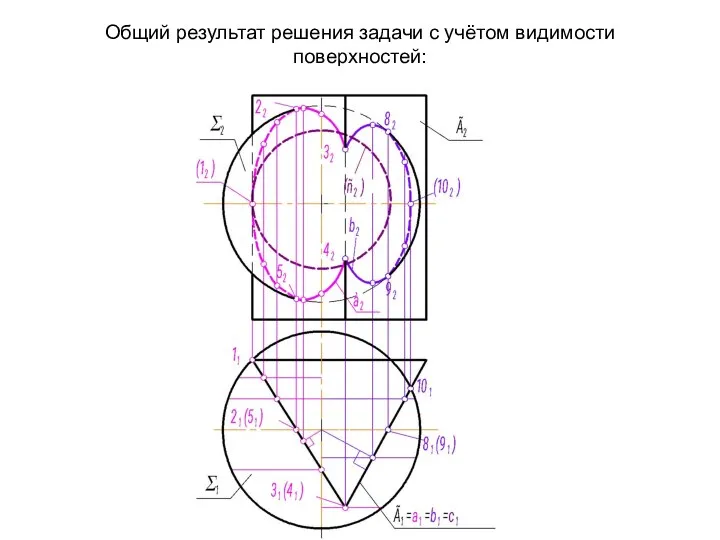
- 47. Общий результат решения задачи с учётом видимости поверхностей:
- 48. Алгоритм: Σ ∩ Г = а, b, с. Г ⊥⊥ П1. 2 ГПЗ, 2 алгоритм. 1.
- 49. Решение задач в случае, когда обе пересекающиеся фигуры - непроецирующие. 3 алгоритм
- 50. В данном случае задача усложняется тем, что на чертеже нет главной проекции ни у одной из
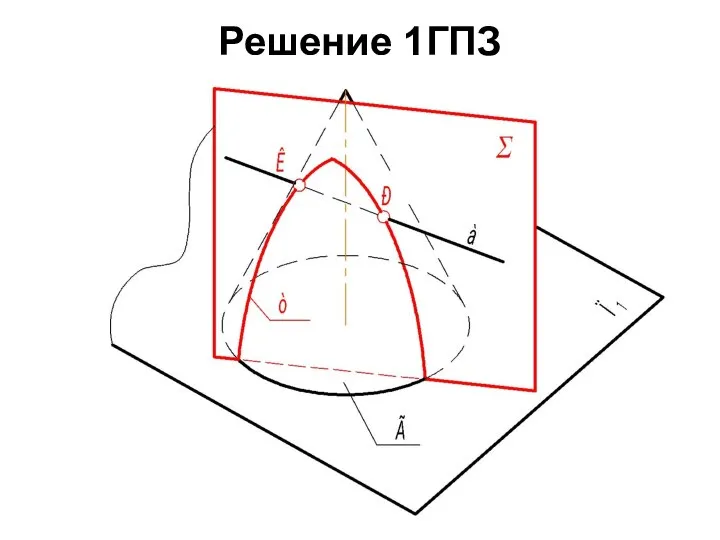
- 51. Решение 1ГПЗ
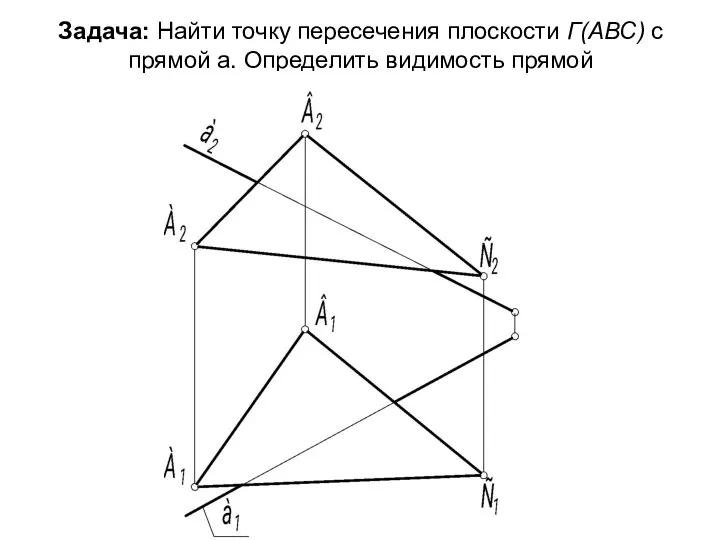
- 52. Задача: Найти точку пересечения плоскости Г(АВС) с прямой а. Определить видимость прямой
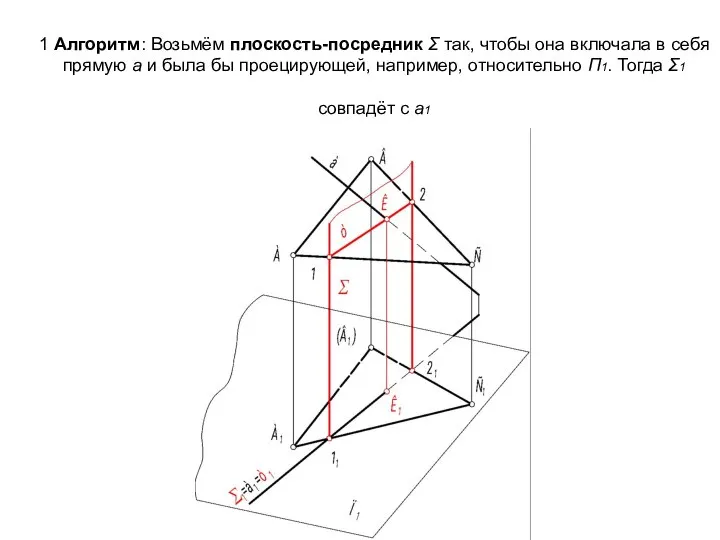
- 53. 1 Алгоритм: Возьмём плоскость-посредник Σ так, чтобы она включала в себя прямую а и была бы
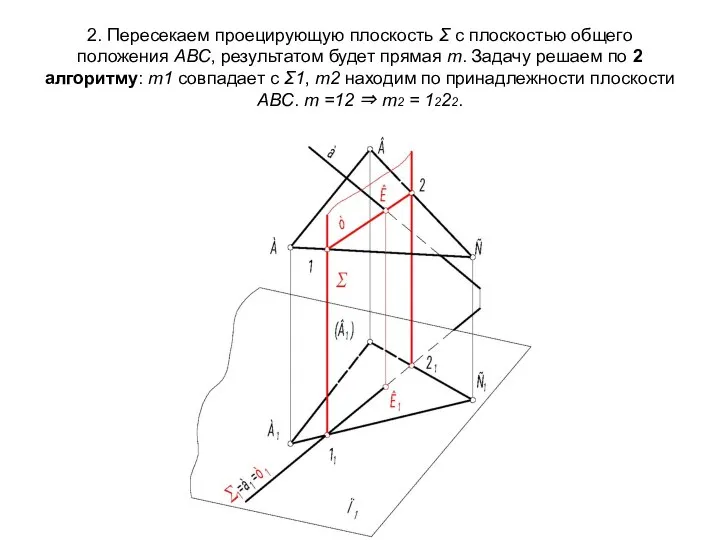
- 54. 2. Пересекаем проецирующую плоскость Σ с плоскостью общего положения АВС, результатом будет прямая m. Задачу решаем
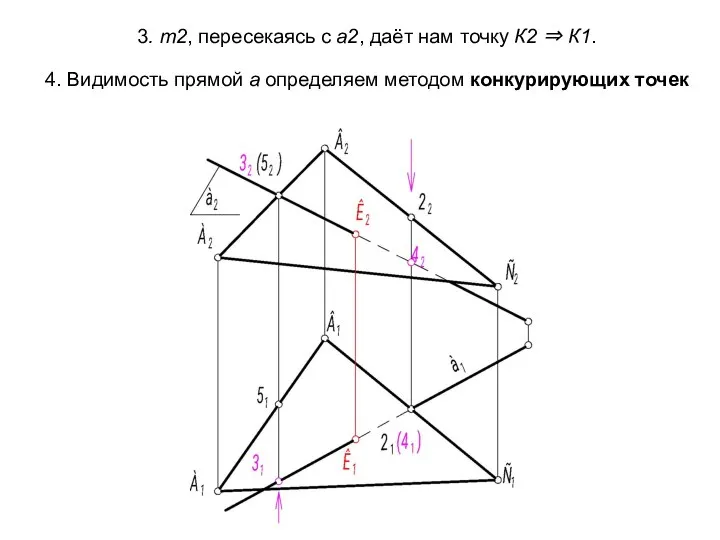
- 55. 3. m2, пересекаясь с а2, даёт нам точку К2 ⇒ К1. 4. Видимость прямой а определяем
- 56. Выполним краткую алгоритмическую запись решения задачи: Г(АВС) ∩ а = К. 1 ГПЗ, 3 алгоритм. Σ
- 57. Такой алгоритм решения приемлем для нахождения точек пересечения любой поверхности с прямой линией. Разница заключается в
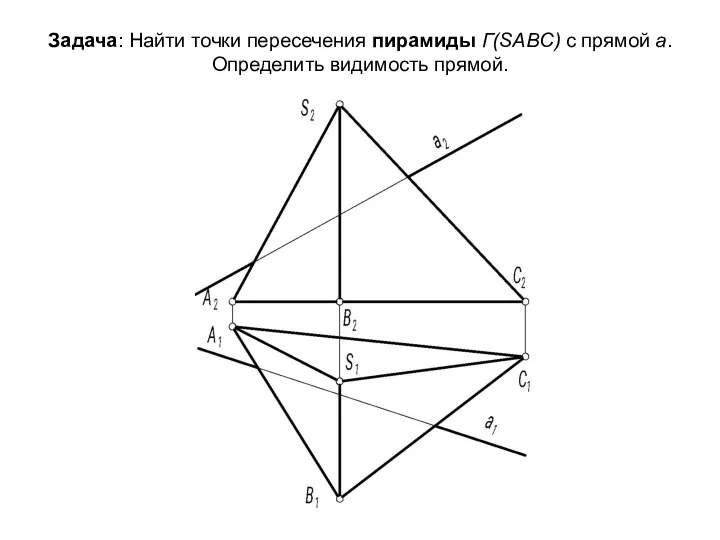
- 58. Задача: Найти точки пересечения пирамиды Г(SABC) с прямой а. Определить видимость прямой.
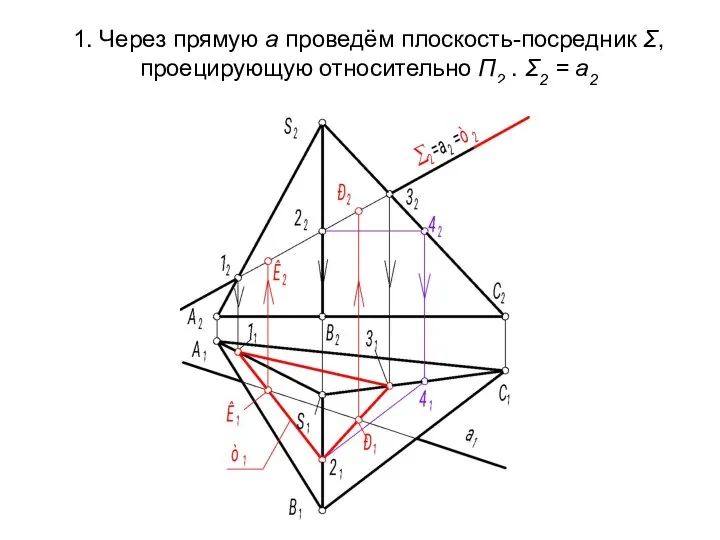
- 59. 1. Через прямую а проведём плоскость-посредник Σ, проецирующую относительно П2 . Σ2 = а2
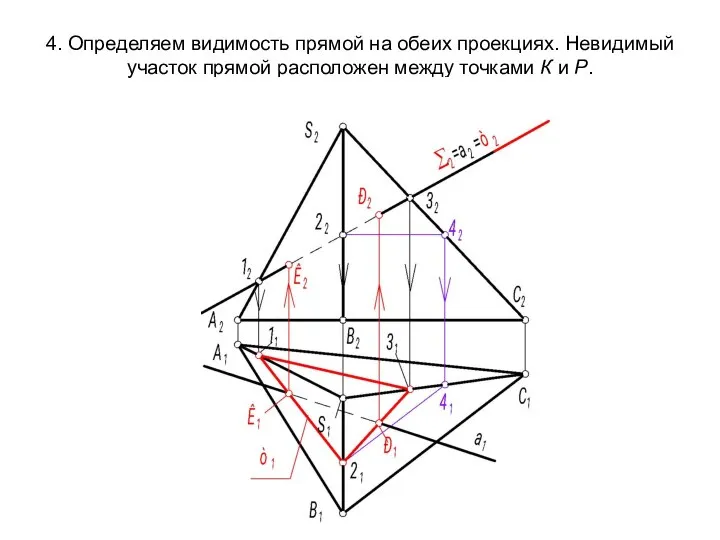
- 60. 4. Определяем видимость прямой на обеих проекциях. Невидимый участок прямой расположен между точками К и Р.
- 61. Алгоритм решения: Г(SABC) ∩ a = K ,P. 1 ГПЗ, 3 алгоритм. 1. Σ - плоскость-посредник,
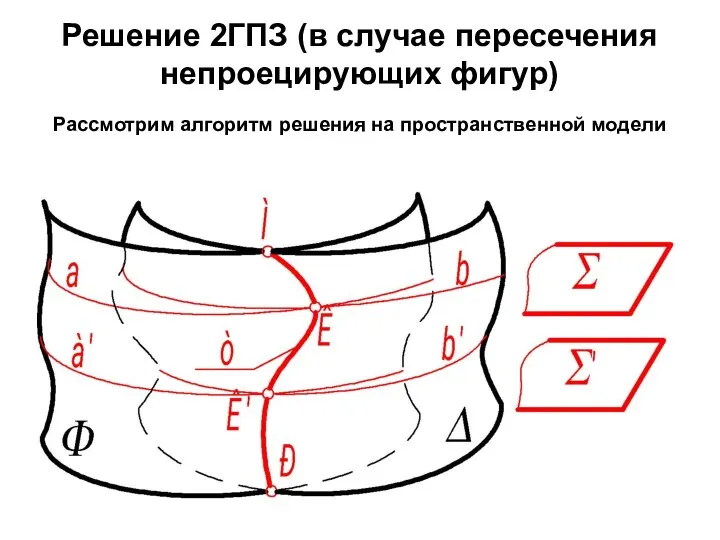
- 62. Решение 2ГПЗ (в случае пересечения непроецирующих фигур) Рассмотрим алгоритм решения на пространственной модели
- 63. Алгоритм решения 1. Ф ∩ Δ = m; 2ГПЗ, 3 алгоритм . 2. Отмечаем очевидные точки
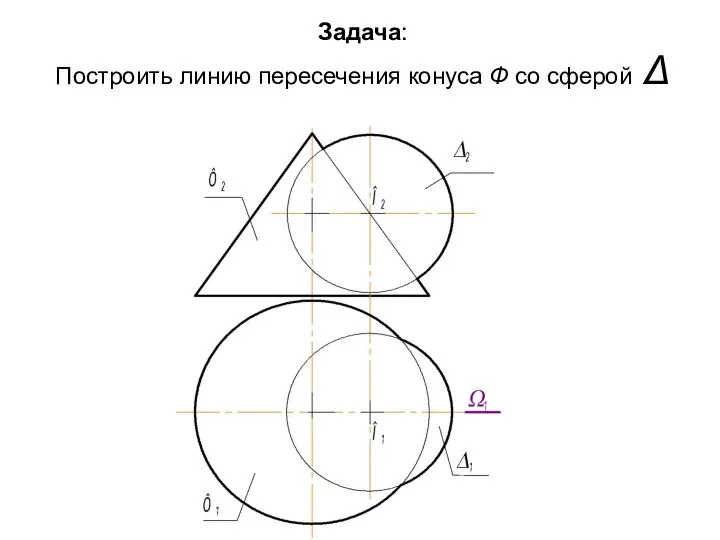
- 64. Задача: Построить линию пересечения конуса Ф со сферой Δ
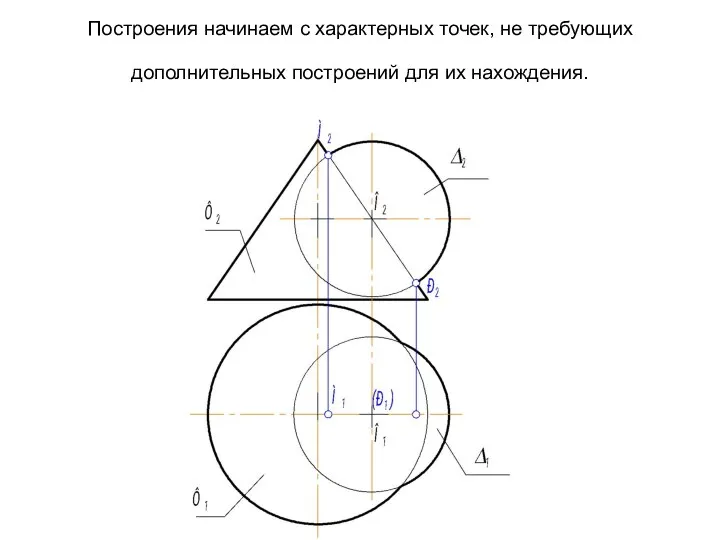
- 65. Построения начинаем с характерных точек, не требующих дополнительных построений для их нахождения.
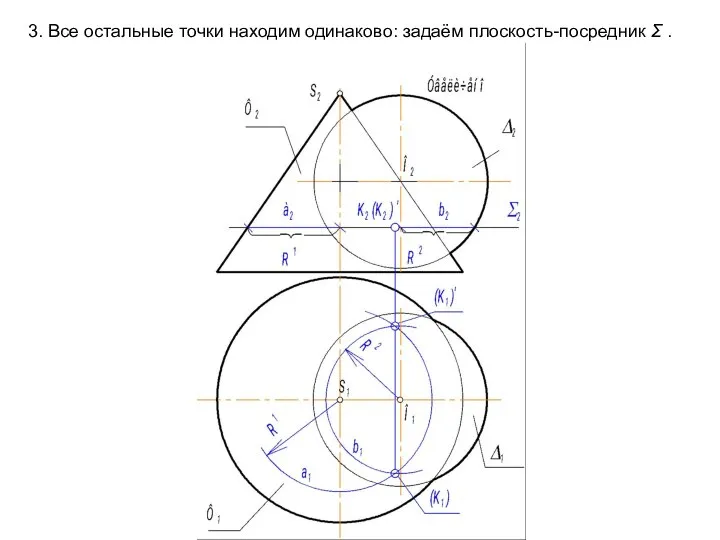
- 66. 3. Все остальные точки находим одинаково: задаём плоскость-посредник Σ .
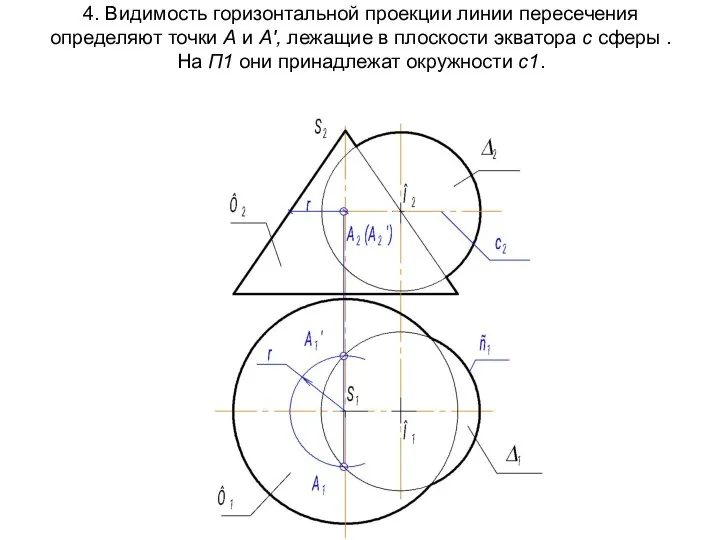
- 67. 4. Видимость горизонтальной проекции линии пересечения определяют точки А и А', лежащие в плоскости экватора с
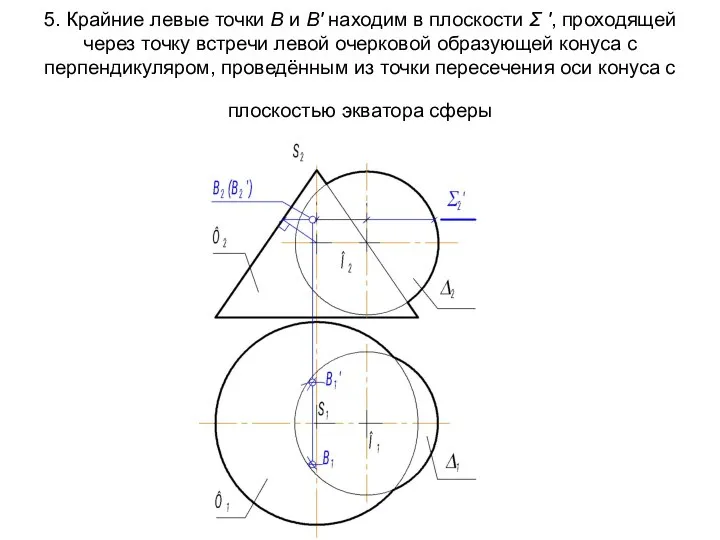
- 68. 5. Крайние левые точки В и В' находим в плоскости Σ ', проходящей через точку встречи
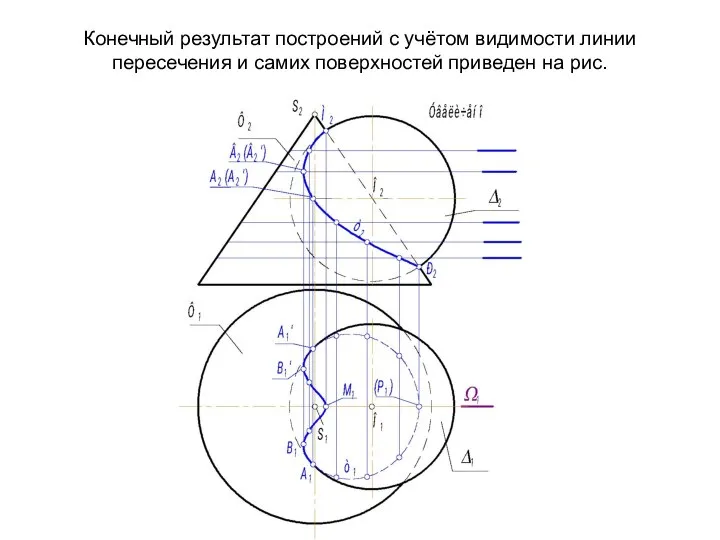
- 69. Конечный результат построений с учётом видимости линии пересечения и самих поверхностей приведен на рис.
- 70. Алгоритмическая запись решения: Ф ∩ Δ = m. 2ГПЗ, 3 алгоритм . 1. Точки М и
- 71. Частные случаи пересечения поверхностей вращения второго порядка Пересечение соосных поверхностей вращения
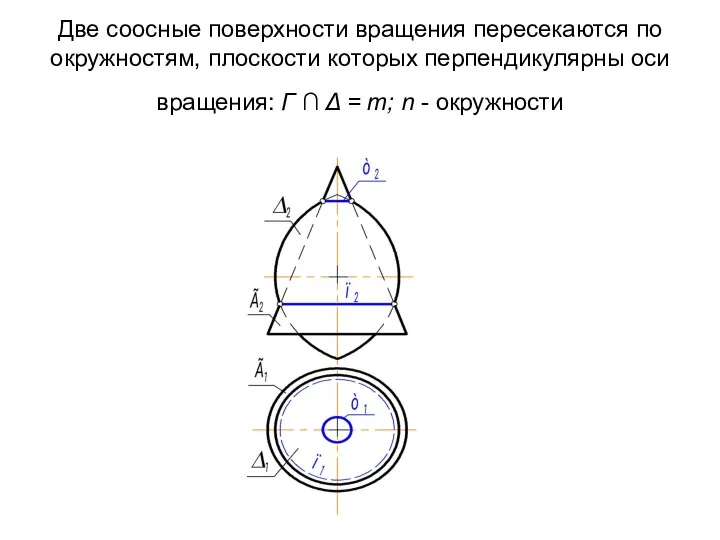
- 72. Две соосные поверхности вращения пересекаются по окружностям, плоскости которых перпендикулярны оси вращения: Г ∩ Δ =
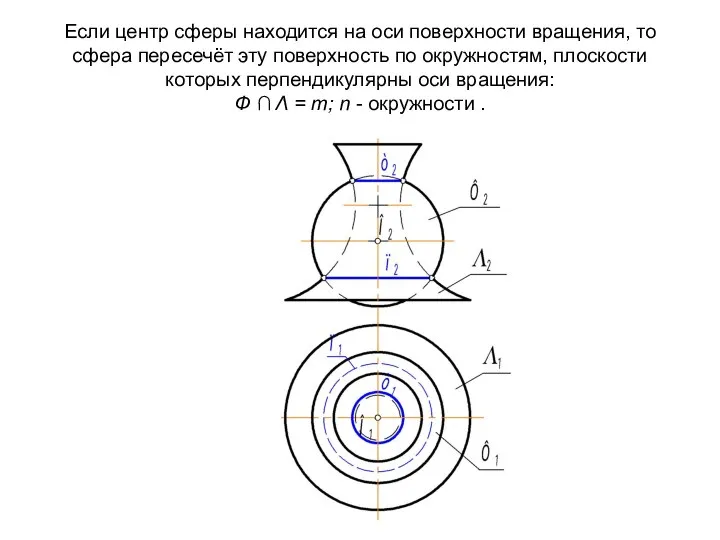
- 73. Если центр сферы находится на оси поверхности вращения, то сфера пересечёт эту поверхность по окружностям, плоскости
- 74. Теорема Монжа Если две поверхности вращения второго порядка описаны около третьей поверхности вращения второго порядка, или
- 76. Скачать презентацию




























 Тема урока: «Десятичные дроби. Действия с десятичными дробями.» 5 класс МОУ «Лотошинская средняя общеобразовательная школа №1»
Тема урока: «Десятичные дроби. Действия с десятичными дробями.» 5 класс МОУ «Лотошинская средняя общеобразовательная школа №1» Презентация на тему Отрезок. Прямая. Луч
Презентация на тему Отрезок. Прямая. Луч Презентация по математике "Занимательные задачи" - скачать бесплатно
Презентация по математике "Занимательные задачи" - скачать бесплатно Математические методы физики волновых явлений, теория. (Лекция 5)
Математические методы физики волновых явлений, теория. (Лекция 5) История Кремля в математике и литературе
История Кремля в математике и литературе Решения линейных уравнений, содержащих знак модуля
Решения линейных уравнений, содержащих знак модуля Рефлексия. Графический диктант
Рефлексия. Графический диктант Графический метод решения системы уравнений с двумя переменными. 7 класс
Графический метод решения системы уравнений с двумя переменными. 7 класс Сравнение значений выражений
Сравнение значений выражений Действия с десятичными дробями
Действия с десятичными дробями Окружность и круг
Окружность и круг Применение теории вероятностей в анализе спортивных событий
Применение теории вероятностей в анализе спортивных событий Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями Теория Множеств
Теория Множеств Логарифмы. Решение логарифмических уравнений и неравенств
Логарифмы. Решение логарифмических уравнений и неравенств Функции многих переменных (ФМП). Частные производные функции двух переменных
Функции многих переменных (ФМП). Частные производные функции двух переменных Признаки делимости на 9 и на 3
Признаки делимости на 9 и на 3 Решение задания В8. Основные типы заданий
Решение задания В8. Основные типы заданий Коррекция зрительной памяти детей младшего школьного возраста с задержкой психического развития на уроках математики
Коррекция зрительной памяти детей младшего школьного возраста с задержкой психического развития на уроках математики Марковские цепи
Марковские цепи Решение неравенств
Решение неравенств Летим в математическую галактику
Летим в математическую галактику Интегрирование ФКП
Интегрирование ФКП Аттестационная работа. Площадь треугольника. Урок математики в 5 классе
Аттестационная работа. Площадь треугольника. Урок математики в 5 классе Искусственные и нечеткие нейронные сети
Искусственные и нечеткие нейронные сети Тренажер по арифметике для начальных классов. Задачи на сложение и вычитание
Тренажер по арифметике для начальных классов. Задачи на сложение и вычитание Методика обучения решению сюжетных задач в курсе математики 5-6 классов
Методика обучения решению сюжетных задач в курсе математики 5-6 классов Понятие логарифма
Понятие логарифма