Содержание
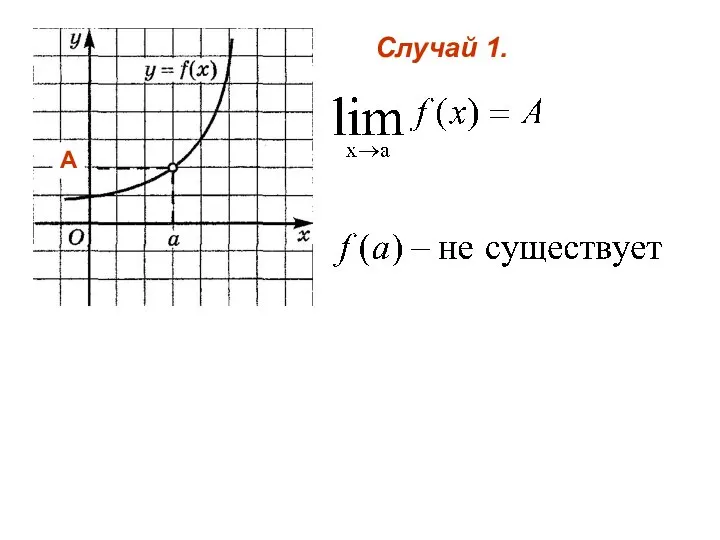
- 2. Случай 1. А
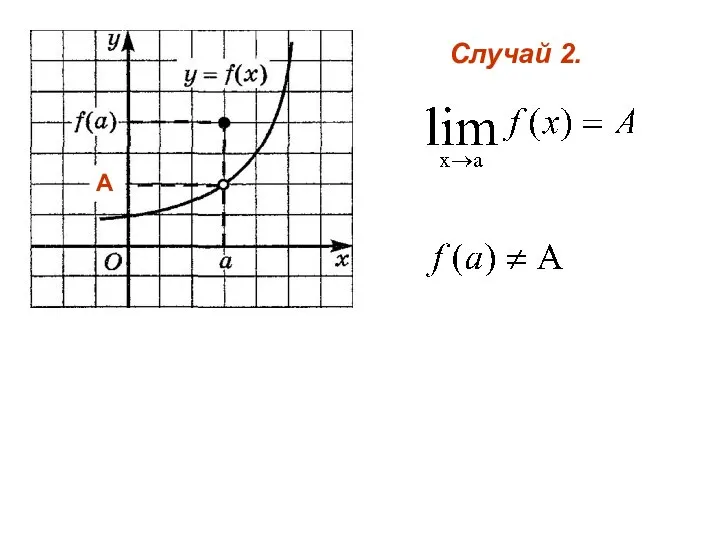
- 3. Случай 2. А
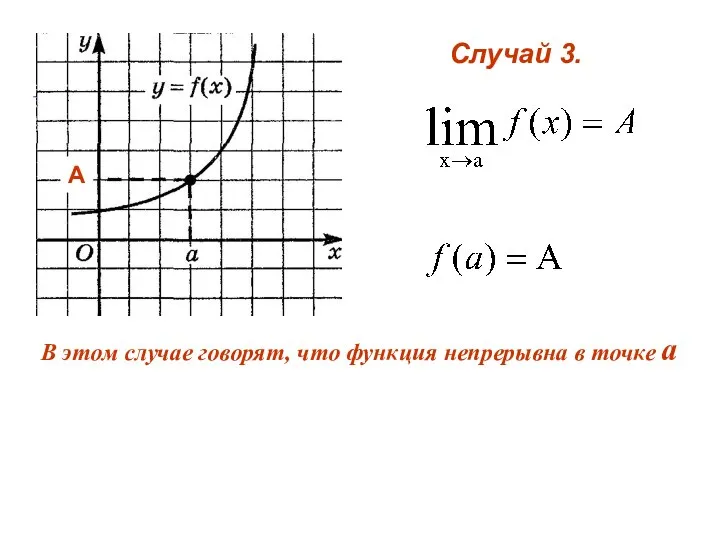
- 4. Случай 3. А В этом случае говорят, что функция непрерывна в точке а
- 5. Предел функции в точке Пусть функция y = f(x) определена в некоторой окрестности точки x0, кроме,
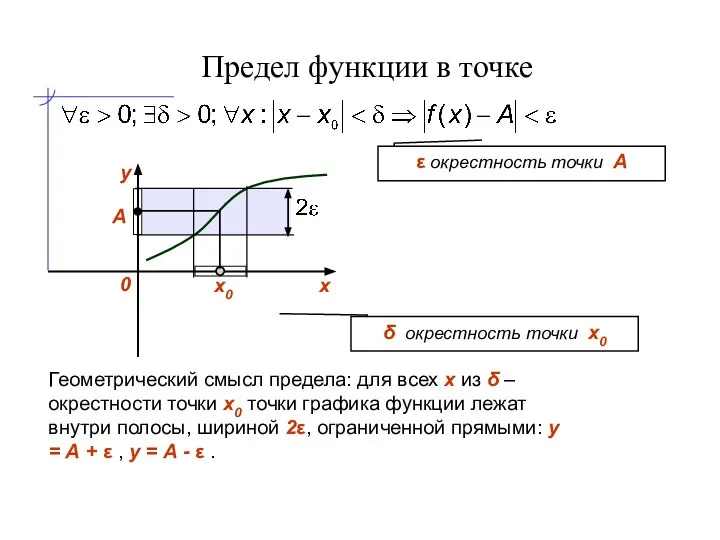
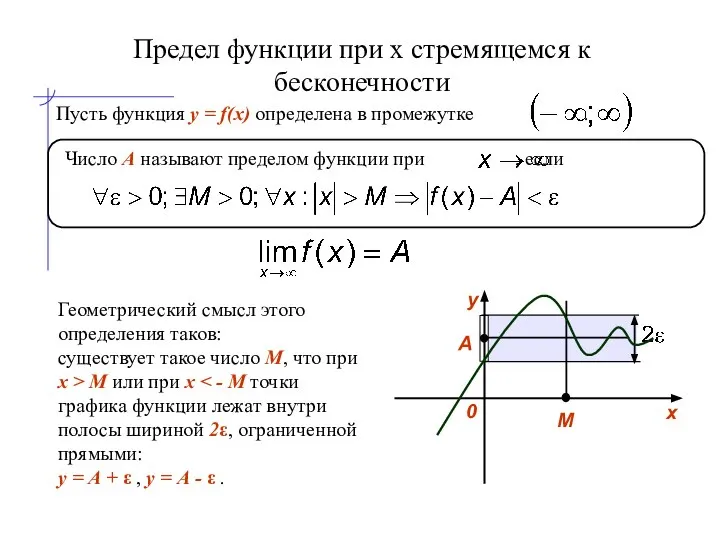
- 6. Предел функции в точке х0 А δ окрестность точки x0 ε окрестность точки А Геометрический смысл
- 7. Односторонние пределы В определении предела функции Бывают случаи, когда способ приближения аргумента x к x0 существенно
- 8. Односторонние пределы Число А2 называют пределом функции справа в точке x0, если Предел справа записывают так:
- 9. Предел функции при x стремящемся к бесконечности Пусть функция y = f(x) определена в промежутке .
- 10. Основные теоремы о пределах Рассмотрим теоремы, которые облегчают нахождение пределов функций. Предел суммы (разности) двух функций
- 11. Основные теоремы о пределах Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя
- 12. Основные теоремы о пределах Если между соответствующими значениями трех функций при этом: тогда: выполняются неравенства: Если
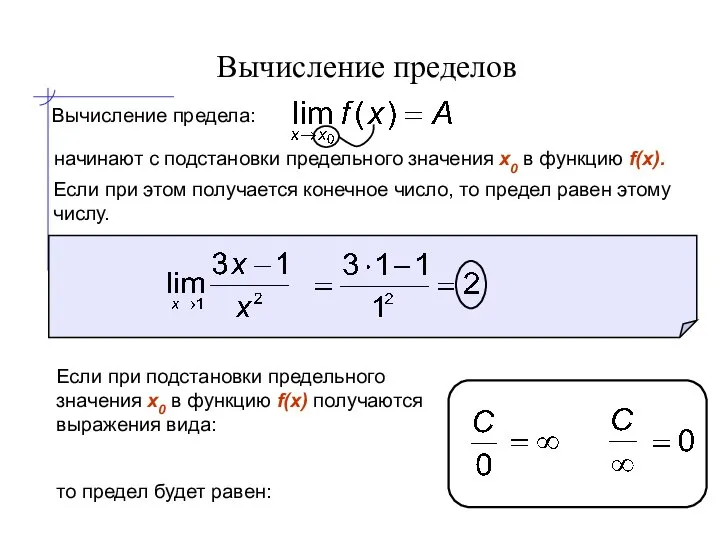
- 13. Вычисление пределов Вычисление предела: начинают с подстановки предельного значения x0 в функцию f(x). Если при этом
- 14. Вычисление пределов Часто при подстановке предельного значения x0 в функцию f(x) получаются выражения следующих видов: Эти
- 15. Раскрытие неопределенностей Раскрытие неопределенности Если f(x) – дробно – рациональная функция, необходимо разложить на множители числитель
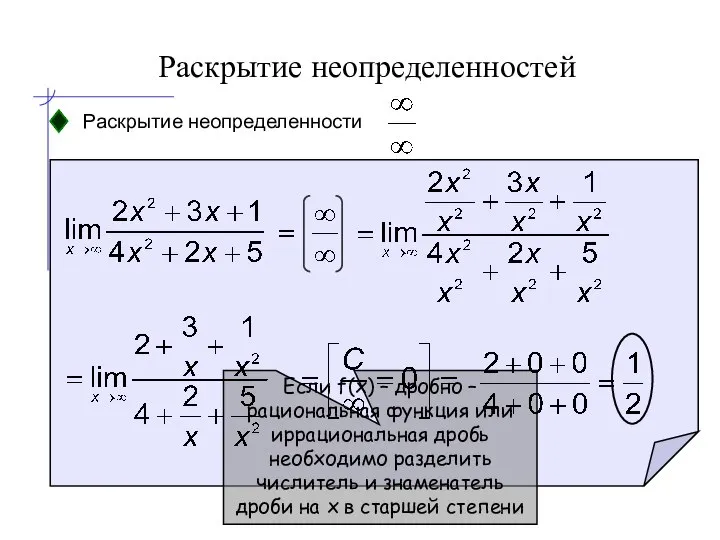
- 16. Раскрытие неопределенностей Раскрытие неопределенности Если f(x) – дробно – рациональная функция или иррациональная дробь необходимо разделить
- 17. Раскрытие неопределенностей Раскрытие неопределенности Умножим и разделим функцию на сопряженное выражение.
- 18. Первый замечательный предел Функция не определена при x = 0. Найдем предел этой функции при О
- 19. Первый замечательный предел О А В С М x
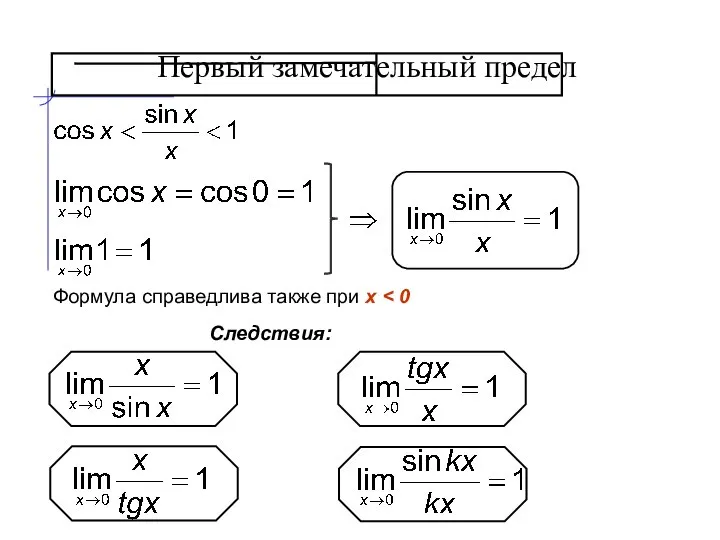
- 20. Первый замечательный предел Следствия: Формула справедлива также при x
- 22. Скачать презентацию











 Двугранный и многогранный угол. Представление о правильных многогранниках
Двугранный и многогранный угол. Представление о правильных многогранниках Показательные неравенства. Метод. Рационализации
Показательные неравенства. Метод. Рационализации Логические задачи на сообразительность и смекалку
Логические задачи на сообразительность и смекалку Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Презентация по математике "Действия с дробями" - скачать
Презентация по математике "Действия с дробями" - скачать  Артамонова Л.В. Учитель математики МКОУ «Москаленский лицей»
Артамонова Л.В. Учитель математики МКОУ «Москаленский лицей»  Математика 2 класс Тема. Буквенные выражения Подготовила учитель начальных классов МОУ «ПСОШ» Чермошенцева Е.А.
Математика 2 класс Тема. Буквенные выражения Подготовила учитель начальных классов МОУ «ПСОШ» Чермошенцева Е.А.  Задачи на части и уравнивание 5 класс
Задачи на части и уравнивание 5 класс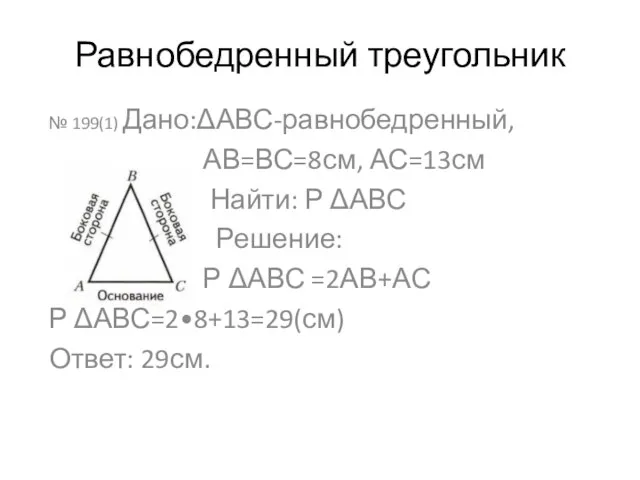 Равнобедренный треугольник
Равнобедренный треугольник Великие математики
Великие математики Средние величины. Понятие средней величины
Средние величины. Понятие средней величины Распределительный метод линейного программирования
Распределительный метод линейного программирования Применение статистических характеристик для создания портрета учащегося МКОУ ХМР СОШ п. Бобровский Фомина Анна Евгеньевна МКОУ
Применение статистических характеристик для создания портрета учащегося МКОУ ХМР СОШ п. Бобровский Фомина Анна Евгеньевна МКОУ  Классическое определение вероятности
Классическое определение вероятности Презентация на тему Сокращение дробей
Презентация на тему Сокращение дробей  Линейные дискретные системы. Описание ЛДС во временной области
Линейные дискретные системы. Описание ЛДС во временной области Статистические методы обработки медико-биологических данных. Нормальный закон распределения
Статистические методы обработки медико-биологических данных. Нормальный закон распределения Интернет-ресурсы в работе учителя математики
Интернет-ресурсы в работе учителя математики Понятие вектора
Понятие вектора Сравнение положительных и отрицательных чисел
Сравнение положительных и отрицательных чисел Прямая и обратная пропорциональнось. Решение задач. Урок закрепления знаний. Е.В.Плотникова, Н.В.Колоколова учителя математики М
Прямая и обратная пропорциональнось. Решение задач. Урок закрепления знаний. Е.В.Плотникова, Н.В.Колоколова учителя математики М Алгоритм перевода десятичной записи числа в запись в позиционной системе с заданным основанием
Алгоритм перевода десятичной записи числа в запись в позиционной системе с заданным основанием Геометрия. Билет 12
Геометрия. Билет 12 Неравенство треугольника
Неравенство треугольника Понятие логарифма, основные свойства логарифмов
Понятие логарифма, основные свойства логарифмов Площадь трапеции
Площадь трапеции Это выучить легко. Значения тригонометрических функций в ладони
Это выучить легко. Значения тригонометрических функций в ладони Солодовникова Наталья Витальевна Солодовникова Наталья Витальевна Учитель начальных классов, МОУ Досатуйская СОШ Приарг
Солодовникова Наталья Витальевна Солодовникова Наталья Витальевна Учитель начальных классов, МОУ Досатуйская СОШ Приарг