Содержание
- 2. Понятие предела функции Определение: Пределом функции y= f(x) называется некоторое число b при x→a. И записывается
- 3. Геометрический смысл предела Определение: Для любого ε>0 можно указать δ-окрестность точки а на оси Ох ,такую
- 4. Геометрический смысл предела (продолжение) Если число b1 есть предел функции y= f(x) при x→a, так что
- 5. Бесконечно малые и большие функции и их свойства Определение: Функция f(x) называется бесконечно малой при x→a
- 6. Свойства бесконечно малых и больших функции Функция обратная по величине бесконечно большой, есть бесконечно малая Функция
- 7. Основные теоремы о пределах Теорема 1: Для того, чтобы число А было пределом функции f(x) при
- 8. Основные теоремы о пределах (продолжение) Теорема 4: Если функция f1(x) и f2(x) имеют приделы при ,
- 9. Неопределенности и методы их решений Неопределенность вида Методы: Разложение числителя и знаменателя на множители с последующим
- 10. Неопределенности и методы их решений Неопределенность вида Методы: Деление на наибольшую степень Предел отношения двух многочленов
- 11. Примеры:
- 12. ТЕОРЕМЫ О ПРЕДЕЛАХ Пусть f(x) и φ(x) – функции, для которых существуют пределы при Тогда справедливы
- 13. ТЕОРЕМА 1. Функция не может иметь более одного предела.
- 14. Предположим обратное: что функция f(x) имеет два предела: А и D, Тогда функцию f(x) можно представить
- 15. Вычитаем почленно эти равенства: Но по условию теоремы а разность является бесконечно малой величиной. Следовательно, предположение
- 16. ТЕОРЕМА 2. Предел алгебраической суммы (разности) конечного числа функций равен сумме (разности) пределов этих функций:
- 17. Доказательство: По условию теоремы: Тогда функции f(x) и φ(x) можно представить как суммы: и Где -
- 18. Сумма бесконечно малых величин является величиной бесконечно малой. Таким образом, функция f(x) + φ(x) представляет собой
- 19. ТЕОРЕМА 3. Предел произведения конечного числа функций равен произведению пределов этих функций:
- 20. Следствие.
- 21. ТЕОРЕМА 4. Предел частного двух функций равен частному пределов этих функций:
- 22. ТЕОРЕМА 5. Если и то предел сложной функции существует и равен
- 23. ТЕОРЕМА 6. Если в некоторой окрестности точки х0 (или при достаточно больших х) то
- 24. Однако из существования пределов суммы, произведения или частного еще не следует, что существуют пределы самих функций
- 25. Пример. Но: - не существует
- 26. Таблица эквивалентности пределов
- 27. Примеры
- 29. Скачать презентацию























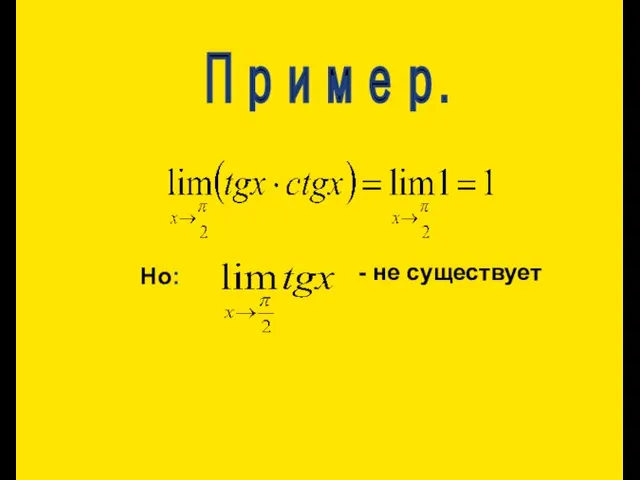


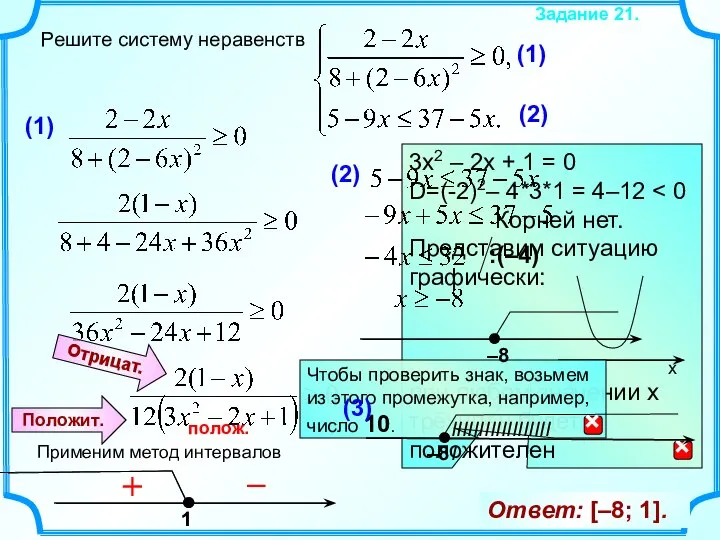 Системы неравенств
Системы неравенств Векторы в пространстве. (11 класс)
Векторы в пространстве. (11 класс) Уравнение окружности
Уравнение окружности Аналитическая геометрия
Аналитическая геометрия Вариант по математике
Вариант по математике Основные понятия теории вероятностей
Основные понятия теории вероятностей Прямоугольный параллелепипед
Прямоугольный параллелепипед Презентация по математике "Обобщение по математике" - скачать бесплатно
Презентация по математике "Обобщение по математике" - скачать бесплатно Математика. Красота и гармония
Математика. Красота и гармония Диофантовы уравнения
Диофантовы уравнения Простейшие задачи в координатах
Простейшие задачи в координатах Презентация по математике "Математические ребусы" - скачать бесплатно
Презентация по математике "Математические ребусы" - скачать бесплатно Треугольники. Элементы треугольника, равнобедренный треугольник, сумма углов треугольника. Повторение, подготовка к ГИА
Треугольники. Элементы треугольника, равнобедренный треугольник, сумма углов треугольника. Повторение, подготовка к ГИА Понятие логарифма. Решить уравнение
Понятие логарифма. Решить уравнение Метод интегрирования по частям в неопределенном интеграле. Интегрирование тригонометрических функций
Метод интегрирования по частям в неопределенном интеграле. Интегрирование тригонометрических функций ОБЪЁМНЫЕ ТЕЛА И МНОГОГРАННИКИ
ОБЪЁМНЫЕ ТЕЛА И МНОГОГРАННИКИ  Свойства умножения. 5 класс
Свойства умножения. 5 класс Исследование операций. Симплексный метод
Исследование операций. Симплексный метод Признаки параллельности прямых. Задачи на готовых чертежах
Признаки параллельности прямых. Задачи на готовых чертежах Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Натуральные числа и дроби. Урок 2
Натуральные числа и дроби. Урок 2 Многочлены от одной переменной
Многочлены от одной переменной Признаки равенства треугольников Третий признак равенства треугольников
Признаки равенства треугольников Третий признак равенства треугольников Аттестационная работа. Методическая разработка по выполнению проекта «Таблица умножения с увлечением»
Аттестационная работа. Методическая разработка по выполнению проекта «Таблица умножения с увлечением» Таблица умножения на 2-10
Таблица умножения на 2-10 Решение заданий №6 (ромб) по материалам открытого банка задач ЕГЭ по математике 2016 года
Решение заданий №6 (ромб) по материалам открытого банка задач ЕГЭ по математике 2016 года Ментальная арифметика в г. Камень-на-Оби
Ментальная арифметика в г. Камень-на-Оби Моделирование систем. 2 лекция ББИ
Моделирование систем. 2 лекция ББИ