Содержание
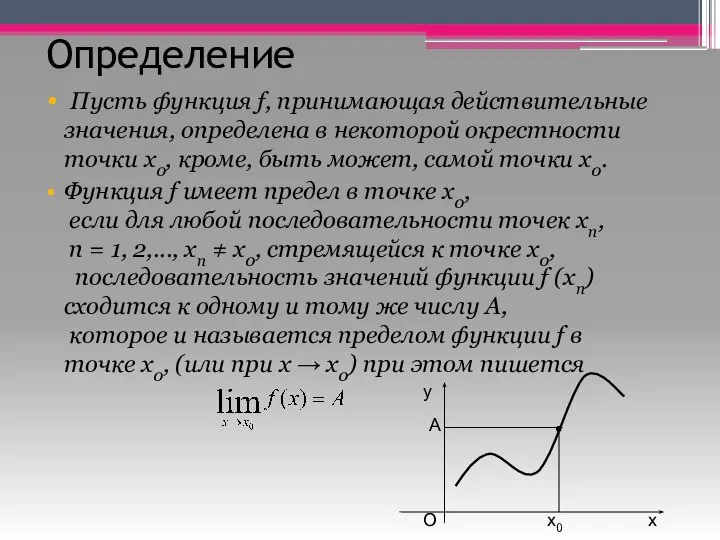
- 2. Определение Пусть функция f, принимающая действительные значения, определена в некоторой окрестности точки x0, кроме, быть может,
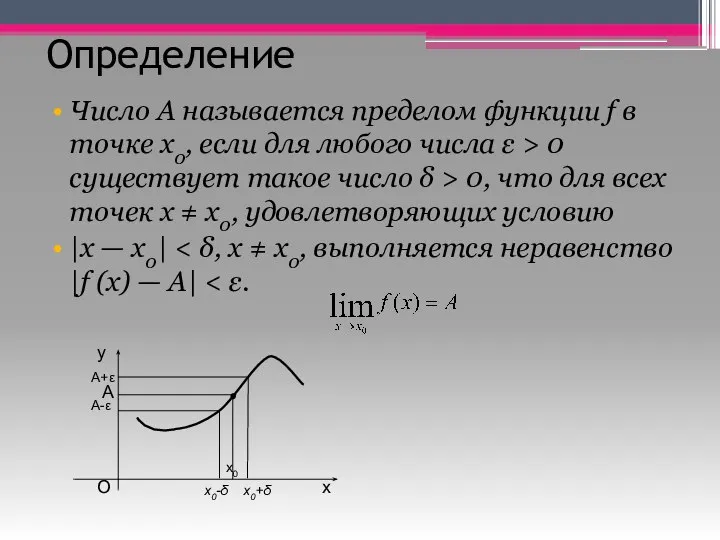
- 3. Определение Число А называется пределом функции f в точке x0, если для любого числа ε >
- 4. Все основные элементарные функции: постоянные, степенная функция (хα), показательная функция (ax), тригонометрические функции (sinx, cosx, tgx
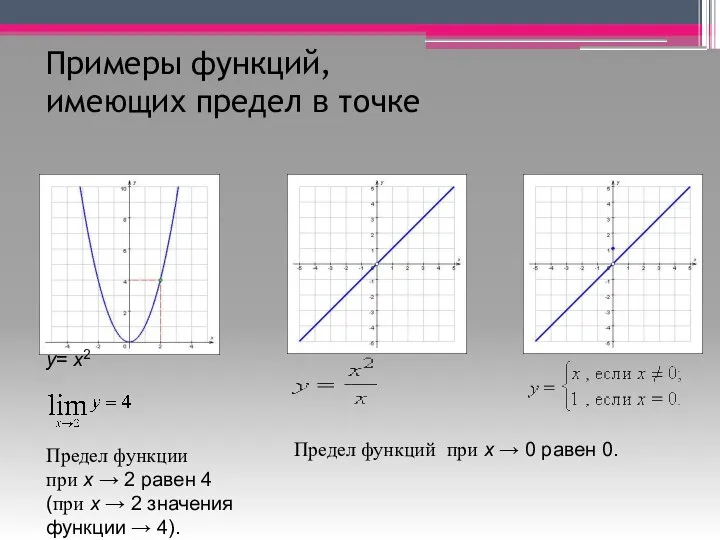
- 5. Примеры функций, имеющих предел в точке у= x2 Предел функции при x → 2 равен 4
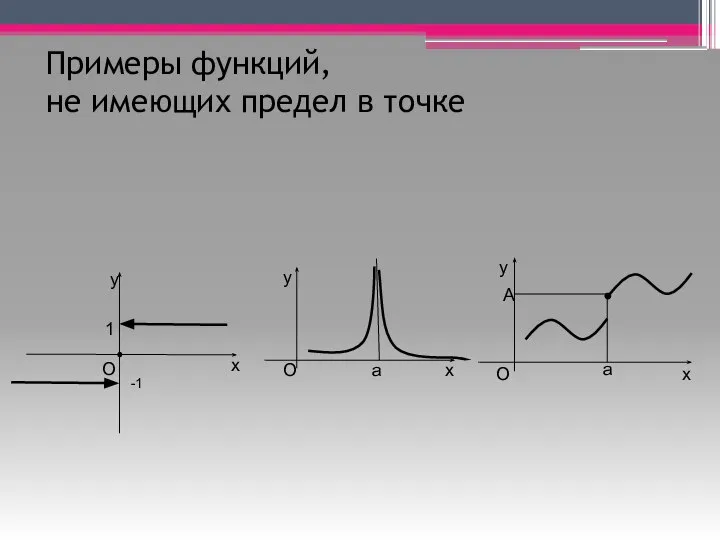
- 6. Примеры функций, не имеющих предел в точке
- 7. Свойства предела функции в точке Если функции f (x) и g (x) имеют конечные пределы в
- 8. Вычисление предела функции в точке Найдем Предел числителя Предел знаменателя . Используя теорему о пределе частного,
- 9. Найдем Предел числителя Предел знаменателя равен нулю, поэтому теорему о пределе частного применять нельзя. Величина 1/(x-3)
- 10. Раскрытие неопределенности При нахождении предела иногда сталкиваются с неопределенностями вида Отыскание предела в таких случаях называется
- 11. Разделим числитель и знаменатель на х4
- 12. Разделим числитель и знаменатель на х2 подразумевается не деление на ноль (делить на ноль нельзя), а
- 13. Вычислить предел Сначала попробуем подставить -1 в дробь: В данном случае получена так называемая неопределенность 0/0
- 14. Метод умножения числителя и знаменателя на сопряженное выражение Найти предел Сначала пробуем подставить 3 в выражение
- 16. Замечательные пределы первый замечательный предел второй замечательный предел
- 17. Примеры
- 18. Односторонние пределы Число A1 называется пределом функции f (x) слева в точке a, если для каждого
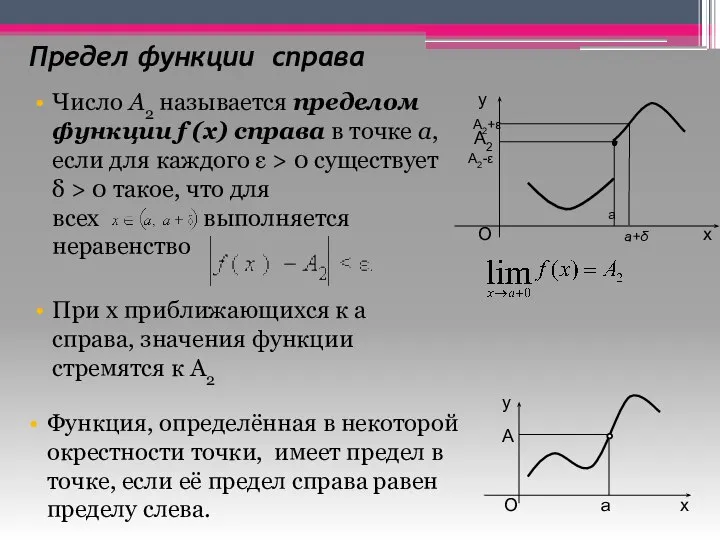
- 19. Предел функции справа Число A2 называется пределом функции f (x) справа в точке a, если для
- 21. Скачать презентацию













 Статистика, часть 6. Условные обозначения
Статистика, часть 6. Условные обозначения Временные ряды
Временные ряды Решение уравнений. Устная работа
Решение уравнений. Устная работа Функция у=кх², её свойства и график
Функция у=кх², её свойства и график Преподавание элементов теории вероятности и статистики в 5-9 классах. Система подготовки учащихся к итоговой аттестации
Преподавание элементов теории вероятности и статистики в 5-9 классах. Система подготовки учащихся к итоговой аттестации Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Профильная математика
Профильная математика Занимательная математика. Числовая окружность
Занимательная математика. Числовая окружность Ряд Фурье
Ряд Фурье Угол между прямыми в пространстве
Угол между прямыми в пространстве Интегральная оценка угрозы биотерроризма. Цели, методы, задачи
Интегральная оценка угрозы биотерроризма. Цели, методы, задачи Scalars, vectors and tensors
Scalars, vectors and tensors Основы статистики. Магия цифр: когда стоит сомневаться в статистике?
Основы статистики. Магия цифр: когда стоит сомневаться в статистике? Прямоугольный параллелепипед
Прямоугольный параллелепипед Задания для устного счёта «Помогите Незнайке» (математика, 2 класс)
Задания для устного счёта «Помогите Незнайке» (математика, 2 класс) Пирамида – это многогранник, составленный из n-угольника
Пирамида – это многогранник, составленный из n-угольника 2D. Геометрические («Параллельность», «Касание», «Концентричность», «Перпендикулярность»)
2D. Геометрические («Параллельность», «Касание», «Концентричность», «Перпендикулярность») Определение многогранника
Определение многогранника Кодирование факторов
Кодирование факторов Моделирование выборочных данных суммой экспоненциальных функций Лекция 12
Моделирование выборочных данных суммой экспоненциальных функций Лекция 12 Определение неизвестного числа
Определение неизвестного числа linear octree
linear octree Решение простейших тригонометрических уравнений. Приемы решения простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений. Приемы решения простейших тригонометрических уравнений Преобразование сумм тригонометрических функций в произведение
Преобразование сумм тригонометрических функций в произведение Вневписанная окружность
Вневписанная окружность Решение задач по теории вероятности, по материалам открытого банка задач ЕГЭ по математике
Решение задач по теории вероятности, по материалам открытого банка задач ЕГЭ по математике Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Трапеция. Математическое исследование
Трапеция. Математическое исследование