Решение простейших тригонометрических уравнений. Приемы решения простейших тригонометрических уравнений

Содержание.

Вводная часть, повторение теоретического материала.
Решение тригонометрических уравнений.
Проблемы, возникающие при решении

ЦЕЛЬ:

Повторить решение тригонометрических
уравнений.
1. Знать формулы для решения простейших

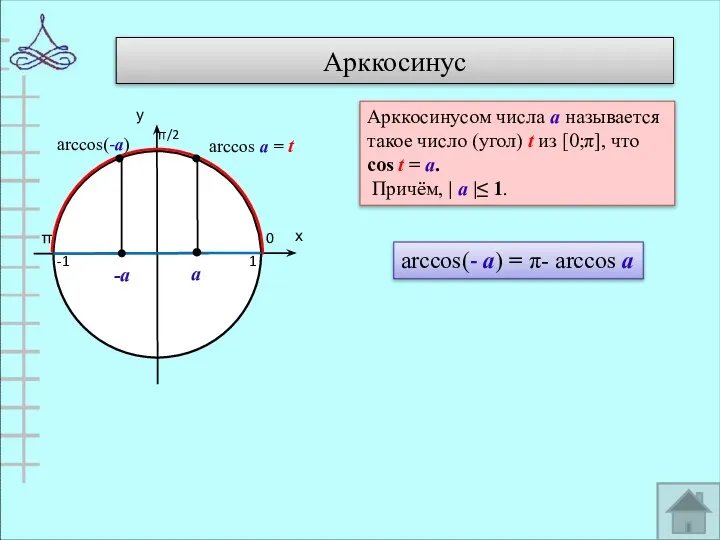
Арккосинус

0

π

1

-1

arccos(-а)

Арккосинусом числа а называется
такое число (угол) t из [0;π], что
cos

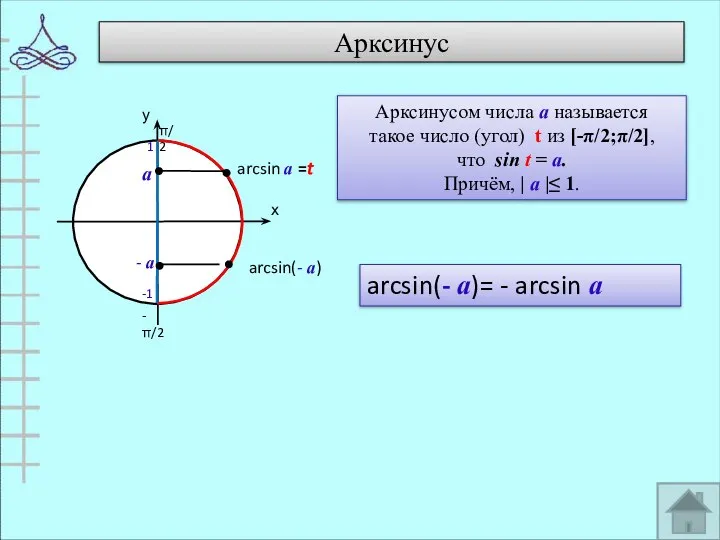
Арксинус

а

- а

arcsin(- а)= - arcsin а

Арксинусом числа а называется
такое

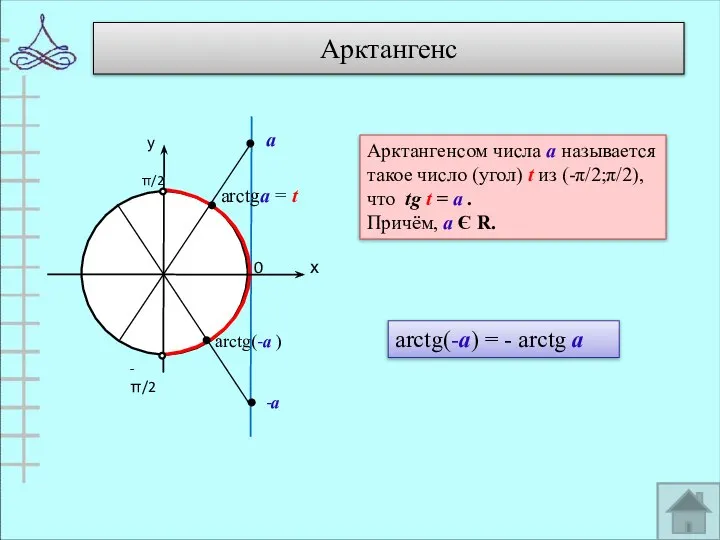
Арктангенс

0

arctgа = t

Арктангенсом числа а называется
такое число (угол) t из (-π/2;π/2),

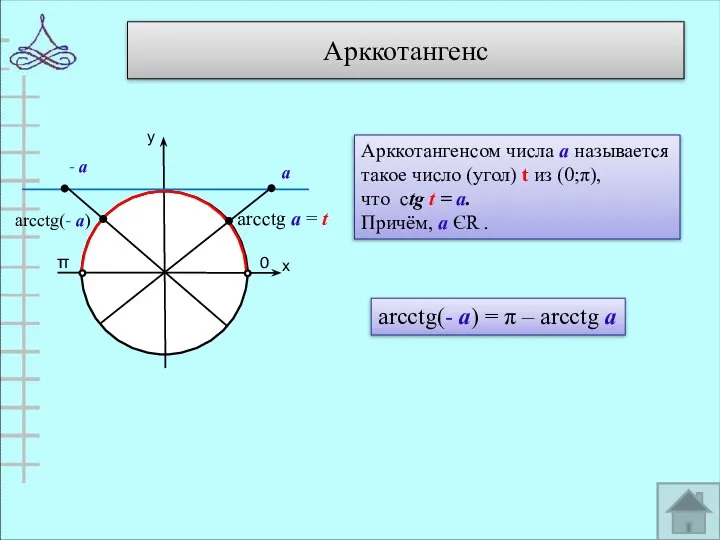
Арккотангенс

у

х

0

π

arcctg а = t

Арккотангенсом числа а называется
такое число (угол) t из

Формулы корней простейших тригонометрических уравнений

2. sint = а, где | а

Формулы корней простейших тригонометрических уравнений

3. tgt = а, аЄR
t =

Примеры:

cost= - ;

3) tg3t = 2017;

t= ±arccos(-1/2)+2πk, kЄZ
t= ± + 2πk,

Решение простейших уравнений

tg2x = -1
2x = arctg (-1) + πk,

Методы решения тригонометрических уравнений.

Методы решения тригонометрических уравнений.

Решение.

2.Однородные
1)Однородное уравнение первой степени:
Решаются делением на cos х (или sinx)

2) Однородные уравнения второй степени:
Решаются делением на cos² х (или sin²x)

Решение тригонометрических уравнений по известным алгоритмам

Вариант 1.
На «3»
3 sin x+ 5