Содержание
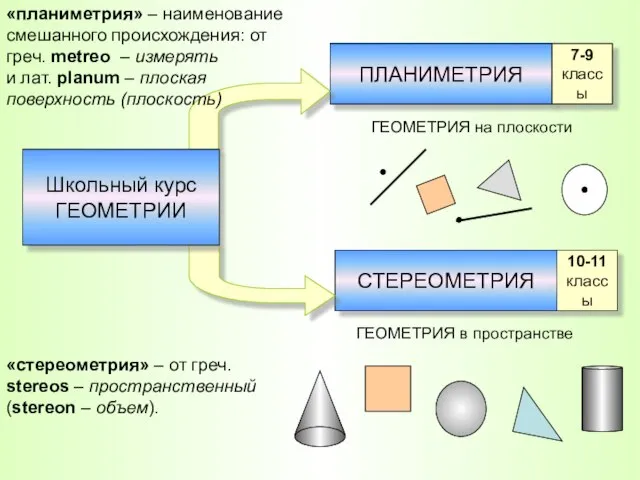
- 2. ПЛАНИМЕТРИЯ СТЕРЕОМЕТРИЯ 7-9 классы 10-11 классы ГЕОМЕТРИЯ на плоскости ГЕОМЕТРИЯ в пространстве «планиметрия» – наименование смешанного
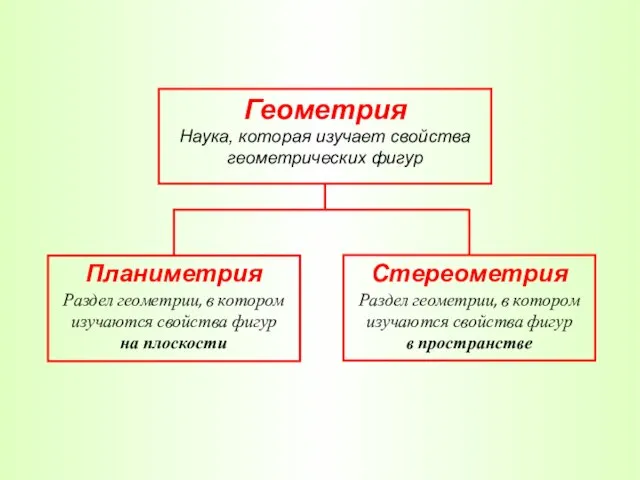
- 3. Геометрия Наука, которая изучает свойства геометрических фигур Планиметрия Стереометрия Раздел геометрии, в котором изучаются свойства фигур
- 4. ГЕОМЕТРИЯ возникла из практических задач людей; ГЕОМЕТРИЯ лежит в основе всей техники и большинства изобретений человечества;
- 5. Изучая СТЕРЕОМЕТРИЮ Мы проведем систематическое рассмотрение свойств геометрических тел в пространстве. Освоим различные способы вычисления практически
- 6. Геометрические фигуры в пространстве называют телами
- 7. Одна и та же фигура допускает различные изображения
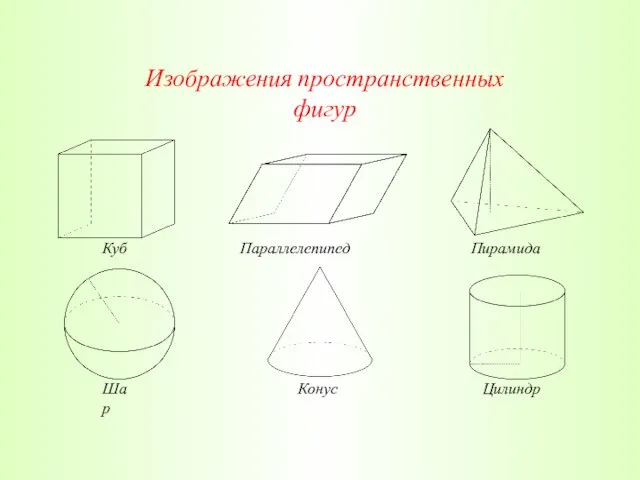
- 8. Изображения пространственных фигур Куб Параллелепипед Пирамида Шар Конус Цилиндр
- 9. Интуитивное, живое пространственное воображение в сочетании со строгой логикой мышления — это ключ к изучению стереометрии
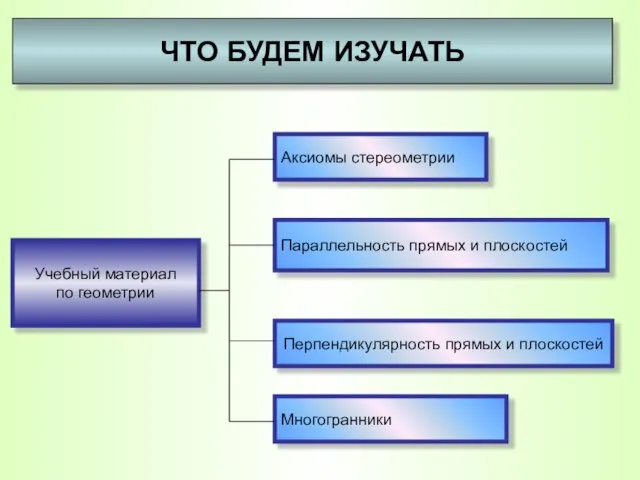
- 10. Учебный материал по геометрии ЧТО БУДЕМ ИЗУЧАТЬ
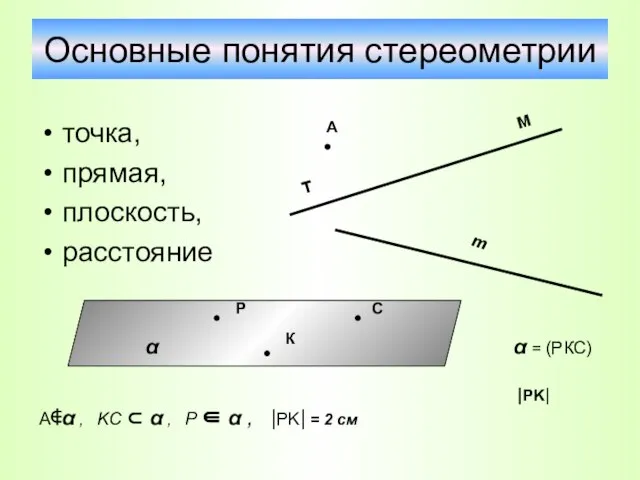
- 11. Основные понятия стереометрии точка, прямая, плоскость, расстояние α = (РКС) |PK| A∉α , KC ⊂ α
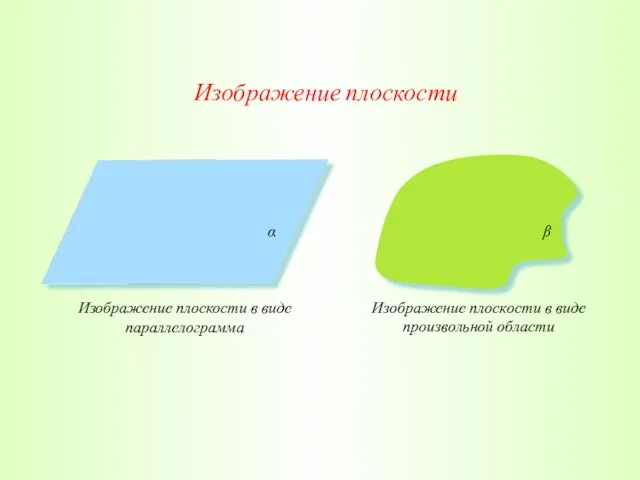
- 12. Изображение плоскости Изображение плоскости в виде параллелограмма Изображение плоскости в виде произвольной области α β
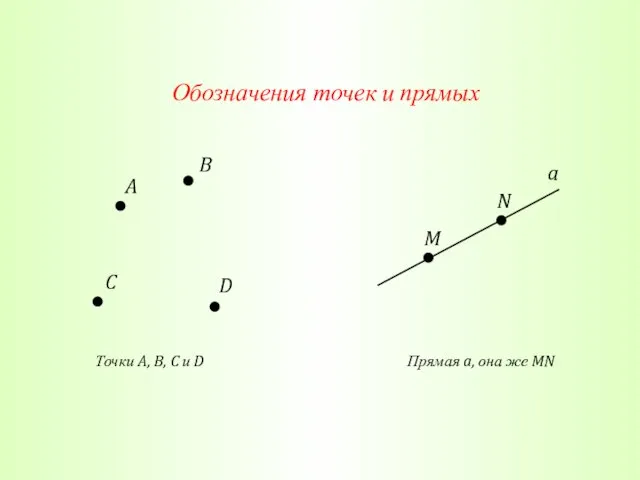
- 13. Обозначения точек и прямых A B C D Точки A, B, C и D M N
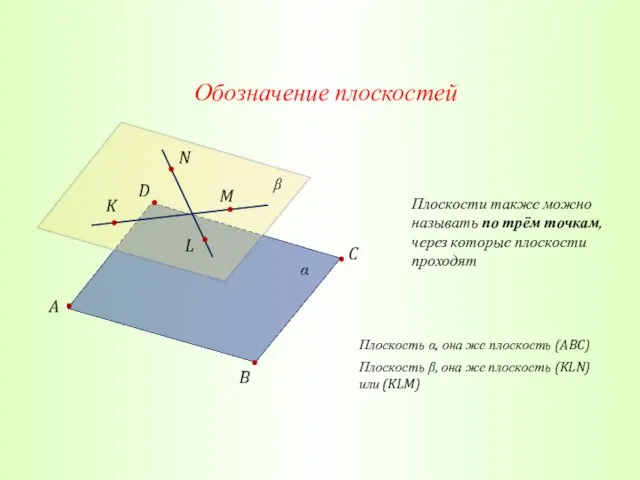
- 14. Обозначение плоскостей A B C D α β K N Плоскость α, она же плоскость (ABC)
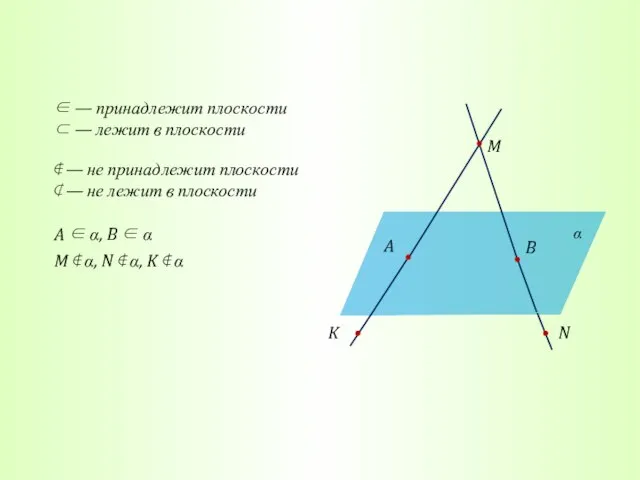
- 15. ∈ — принадлежит плоскости ⊂ — лежит в плоскости ∉ — не принадлежит плоскости ⊄ —
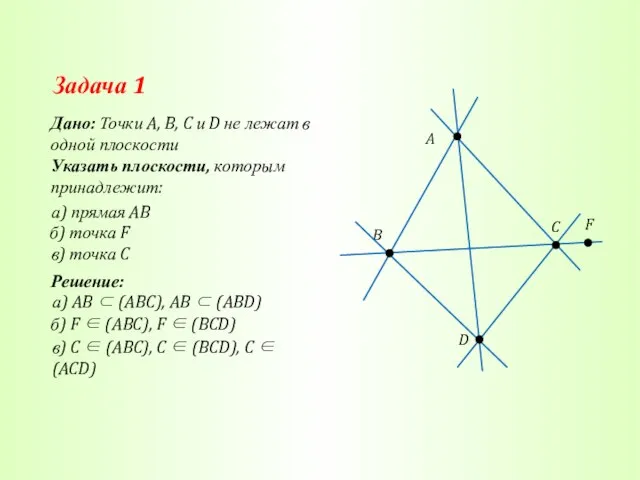
- 16. Задача 1 Дано: Точки A, B, C и D не лежат в одной плоскости Указать плоскости,
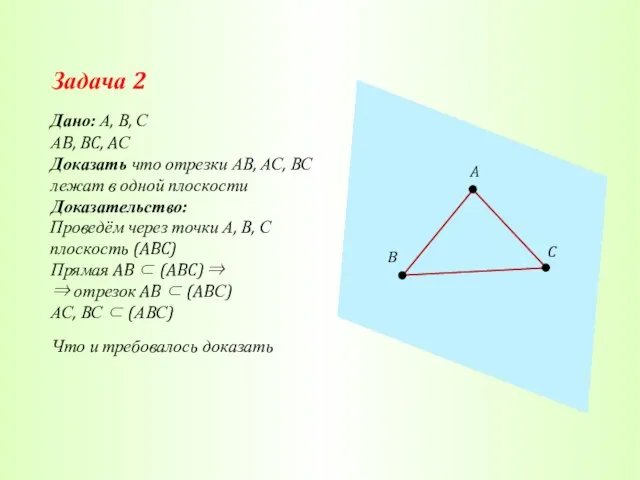
- 17. Задача 2 Дано: А, В, С Доказать что отрезки АВ, АС, ВС лежат в одной плоскости
- 18. Любые три точки лежат в одной плоскости. Любые четыре точки лежат в одной плоскости. Любые четыре
- 19. Аксиомы стереометрии Слово «аксиома» греческого происхождения и в переводе означает истинное, исходное положение теории. Система аксиом
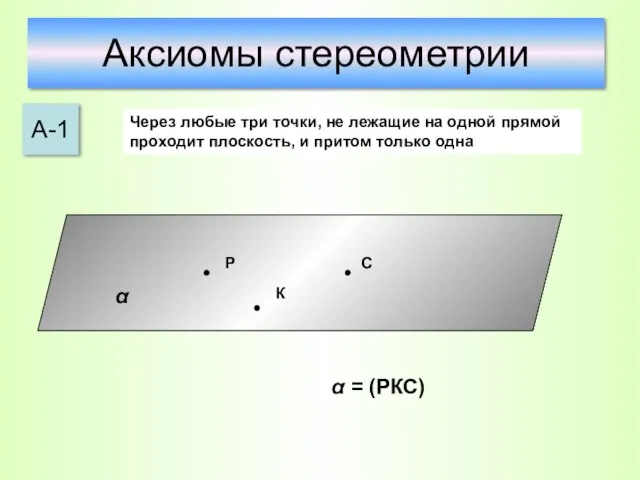
- 20. Аксиомы стереометрии А-1 Через любые три точки, не лежащие на одной прямой проходит плоскость, и притом
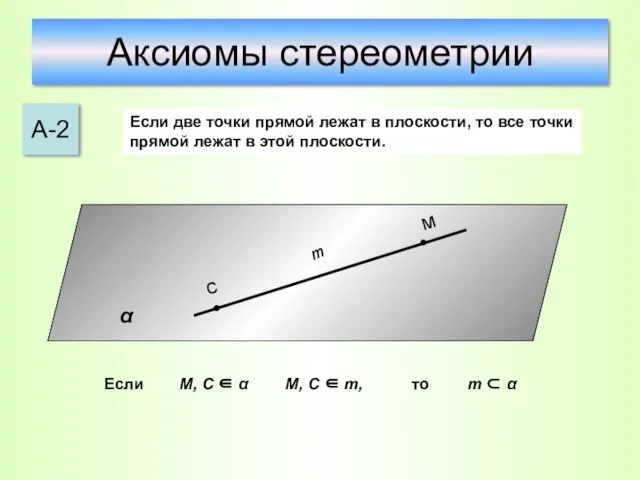
- 21. Аксиомы стереометрии А-2 Если две точки прямой лежат в плоскости, то все точки прямой лежат в
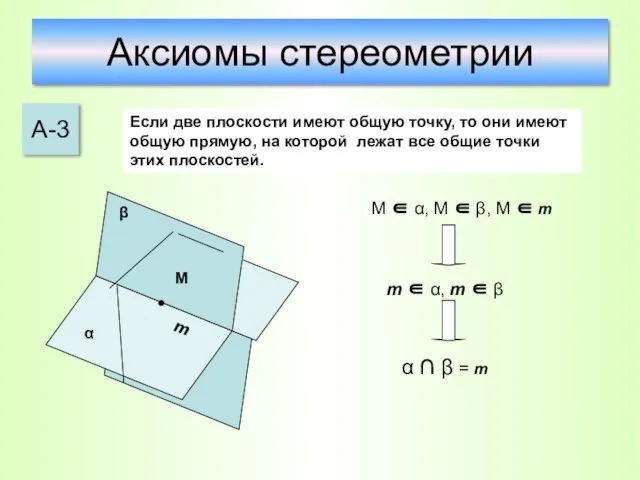
- 22. Аксиомы стереометрии А-3 Если две плоскости имеют общую точку, то они имеют общую прямую, на которой
- 23. СЛЕДСТВИЯ ИЗ АКСИОМ Т-1 Через любую прямую и не принадлежащую ей точку можно провести плоскость, и
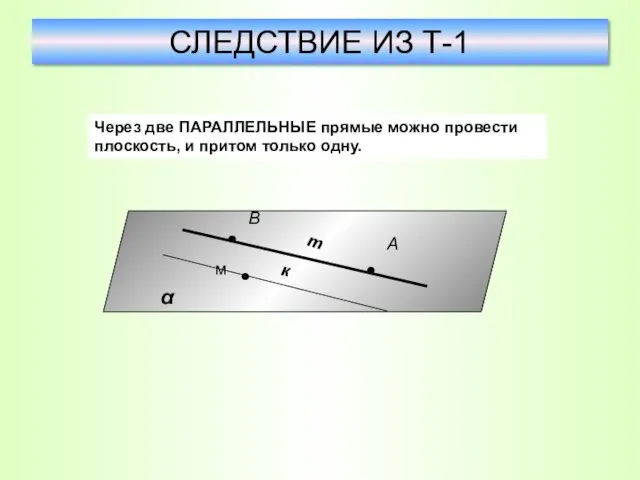
- 24. СЛЕДСТВИЕ ИЗ Т-1 Через две ПАРАЛЛЕЛЬНЫЕ прямые можно провести плоскость, и притом только одну. к
- 25. СЛЕДСТВИЯ ИЗ АКСИОМ Т-2 Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.
- 26. По трем точкам, не лежащим на одной прямой По прямой и точке, не лежащей на этой
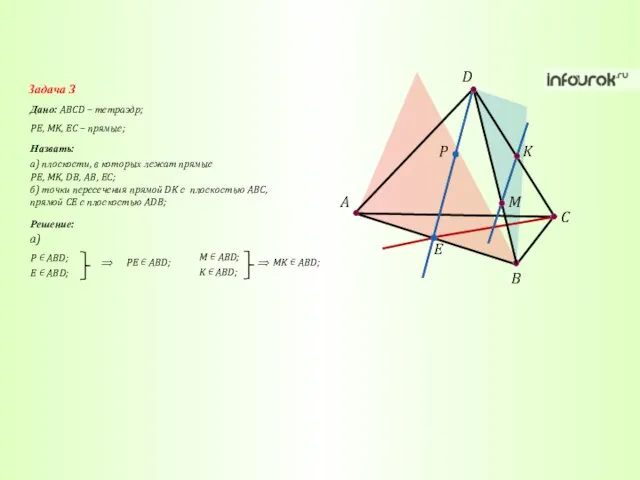
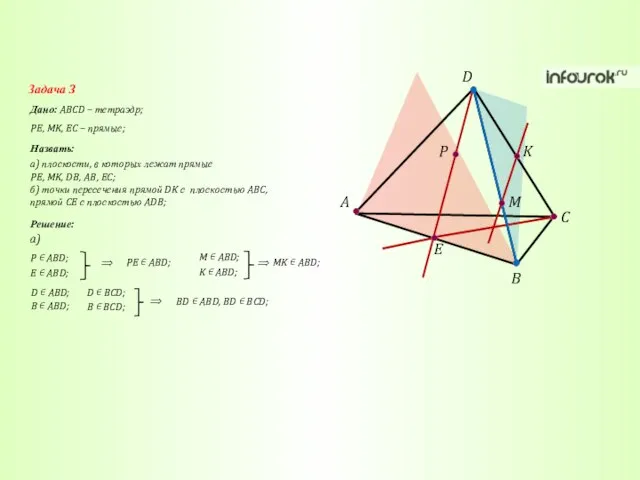
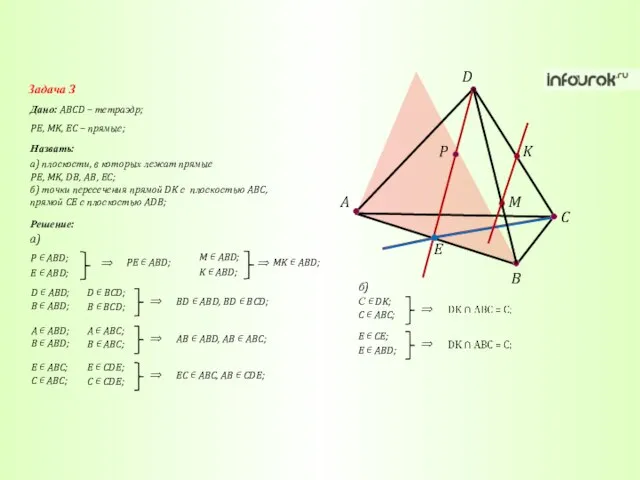
- 27. A C B D K M P E Задача 3 Дано: ABCD – тетраэдр; Назвать: PE,
- 28. A C B D K M P E Задача 3 Дано: ABCD – тетраэдр; Назвать: PE,
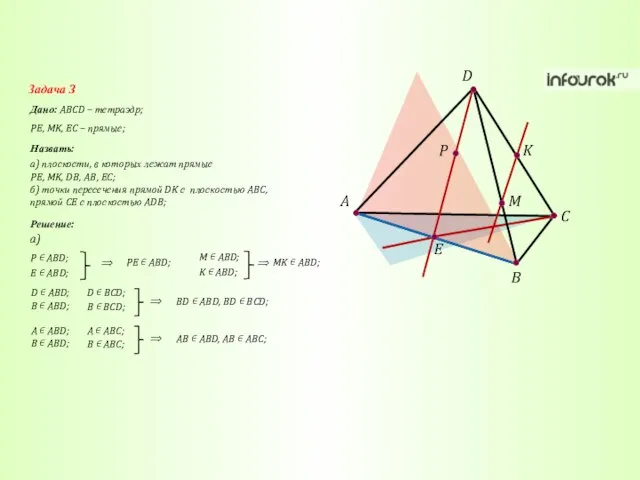
- 29. A C B D K M P E Задача 3 Дано: ABCD – тетраэдр; Назвать: PE,
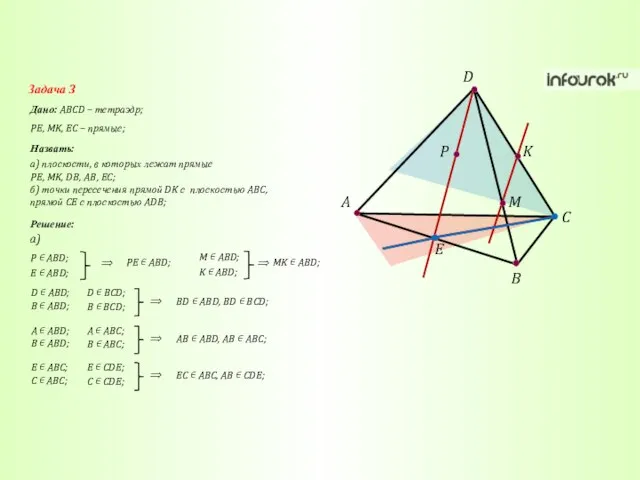
- 30. A C B D K M P E Задача 3 Дано: ABCD – тетраэдр; Назвать: PE,
- 31. A C B D K M P E Задача 3 Дано: ABCD – тетраэдр; Назвать: PE,
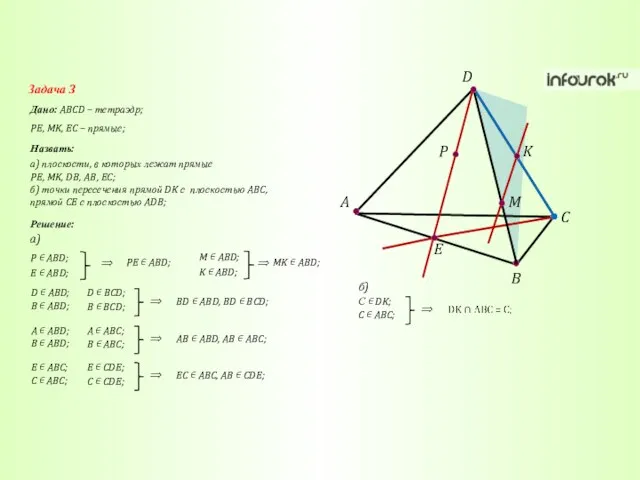
- 32. A C B D K M P E Задача 3 Дано: ABCD – тетраэдр; Назвать: PE,
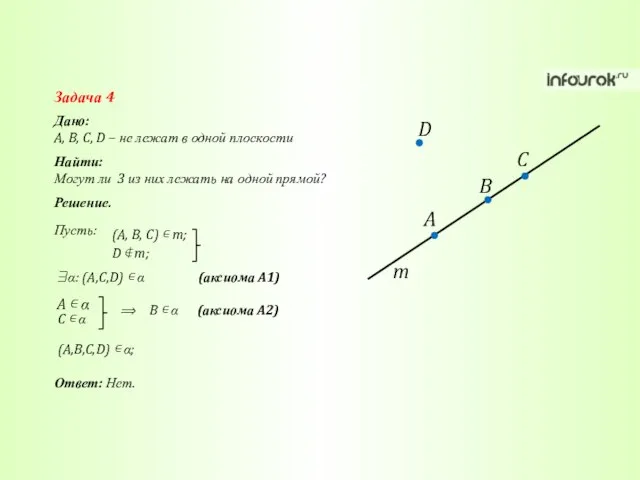
- 33. Дано: A, B, C, D – не лежат в одной плоскости Задача 4 Найти: Могут ли
- 35. Скачать презентацию










 Возрастание и убывание функции
Возрастание и убывание функции Тетраэдр (четырехгранник)
Тетраэдр (четырехгранник) Математическая статистика в жизни нашего класса. МАОУ «СОШ №1» с углублённым изучением отдельных предметов им. И. А. Куратова г. Сы
Математическая статистика в жизни нашего класса. МАОУ «СОШ №1» с углублённым изучением отдельных предметов им. И. А. Куратова г. Сы Теорема Пифагора. Формулировка и доказательство теоремы
Теорема Пифагора. Формулировка и доказательство теоремы Главные направления линии второго порядка
Главные направления линии второго порядка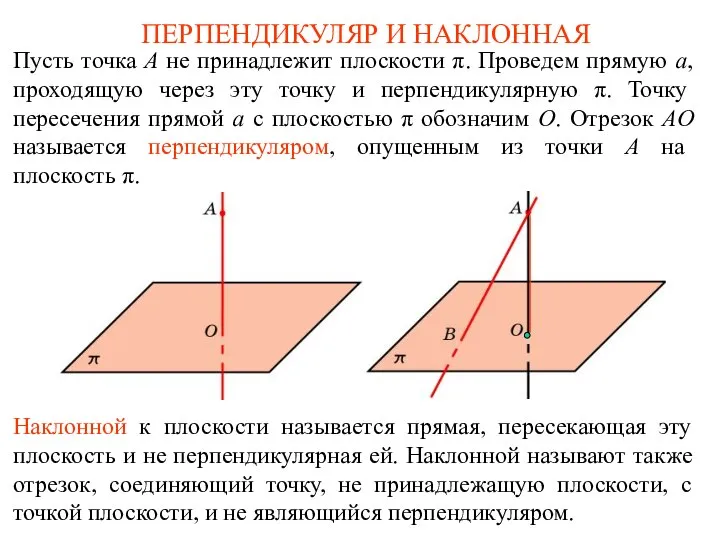 Перпендикуляр и наклонная
Перпендикуляр и наклонная Научно-исследовательская работа по математике ОДНОПАРАМЕТРИЧЕСКИЕ СЕМЕЙСТВА ЛИНИЙ Автор: Гуркин Александр Александрович, МОУ
Научно-исследовательская работа по математике ОДНОПАРАМЕТРИЧЕСКИЕ СЕМЕЙСТВА ЛИНИЙ Автор: Гуркин Александр Александрович, МОУ 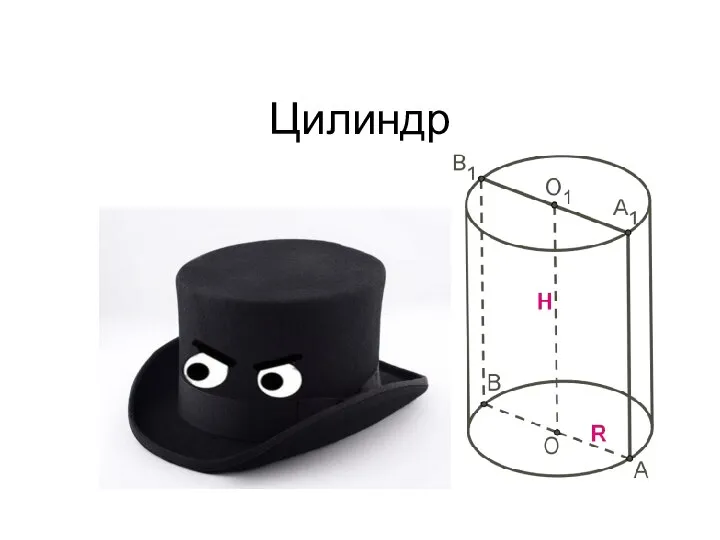 Цилиндр. Формулы цилиндра
Цилиндр. Формулы цилиндра Окружность. Длина окружности
Окружность. Длина окружности Векторы в пространстве
Векторы в пространстве Симметрия. Виды симметрии
Симметрия. Виды симметрии Противоположные числа. Модуль (6 класс)
Противоположные числа. Модуль (6 класс) Первый признак равенства треугольников. Задачи для устной работы
Первый признак равенства треугольников. Задачи для устной работы Презентация по математике "Волшебное приключение" - скачать
Презентация по математике "Волшебное приключение" - скачать  Теоретическая разминка. Десятичные дроби
Теоретическая разминка. Десятичные дроби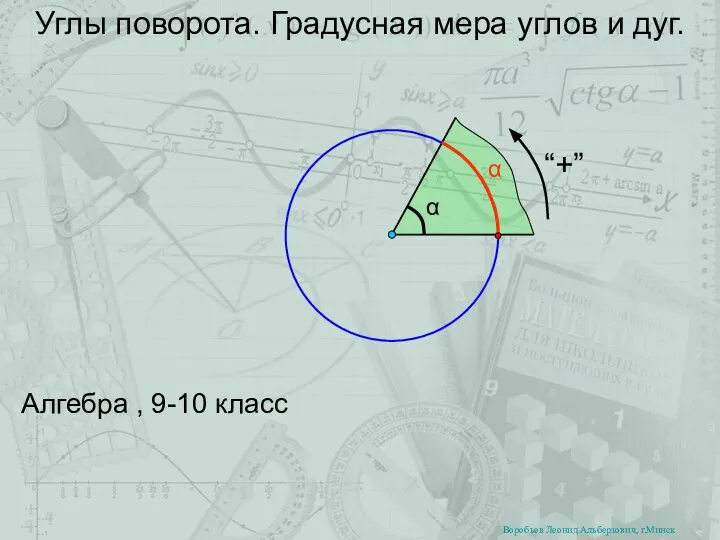 Углы поворота. Градусная мера углов и дуг
Углы поворота. Градусная мера углов и дуг Математический диктант
Математический диктант Измерение углов
Измерение углов Четырехугольники 8 класс
Четырехугольники 8 класс Площадь криволинейной трапеции
Площадь криволинейной трапеции Арифметическая прогрессия вокруг нас (часть 1)
Арифметическая прогрессия вокруг нас (часть 1) Урок математики 5 класс
Урок математики 5 класс  Площадь треугольника
Площадь треугольника Геометрический турнир
Геометрический турнир Тригонометриялық теңдеулерді шешу
Тригонометриялық теңдеулерді шешу Определенный интеграл
Определенный интеграл Мультиколлинеарность. Строгая и нестрогая мультиколлинеарность
Мультиколлинеарность. Строгая и нестрогая мультиколлинеарность Основное свойство дроби. 6 класс
Основное свойство дроби. 6 класс