Содержание
- 2. ПЛАН Обобщенный ряд Фурье Тригонометрический ряд Фурье Понятие о спектре периодической функции Преобразование Фурье для непериодических
- 3. ЛИТЕРАТУРА Поршнев С.В., Беленкова И.В., Численные методы на базе Mathcad. – СПб.: БХВ-Петербург, 2005, – 464
- 4. Периодическая функция с периодом Обобщенный ряд Фурье для периодической функции Скалярное произведение Ортонормированный базис Условие взаимной
- 5. Разложение периодических функций в обобщенный ряд Фурье - обобщенный ряд Фурье для периодической функции В результате
- 6. Тригонометрический ряд Фурье Тригонометрический базис Тригонометрический ряд Фурье Условия разложимости периодической функции в ряд Фурье Функция
- 7. коэффициенты Фурье Тригонометрический ряд Фурье
- 8. коэффициенты Фурье Вывод выражений для коэффициентов Фурье Тригонометрический ряд Фурье Остальные выражения получаются аналогично Скалярное произведение
- 9. Частоты гармоник ряда Фурье основная частота – циклическая частота, соответствующая периоду функции постоянная составляющая = среднее
- 10. Четные и нечетные функции Периодическая функция с периодом Ряд Фурье Четная функция Нечетная функция
- 11. Равенство Парсеваля для ряда Фурье ряд Фурье Равенство Парсеваля Равенство Парсеваля связывает энергию сигнала во временной
- 12. Амплитуды и фазы гармоник гармоника ряда Фурье амплитуда и фаза гармоники Связь с коэффициентами Фурье Эквивалентная
- 13. Ряд Фурье по комплексным экспонентам
- 14. Ряд Фурье по комплексным экспонентам Соотношения для вещественной периодической функции
- 15. Ряд Фурье по комплексным экспонентам Замечание. Отрицательная частота является не физическим, а математическим понятием, вытекающим из
- 16. Преобразование Фурье для непериодических функций комплексная амплитуда гармоники Непериодическая функция может рассматриваться как функция с бесконечно
- 17. Преобразование Фурье. Интеграл Фурье Здесь частоту нельзя определить, как величину, обратную периоду. Частотой теперь будем называть
- 18. Прямое преобразование Фурье Интеграл Фурье Обратное преобразование Фурье - функции, сопряженные по Фурье
- 19. Условия существования интеграла Фурье Функция должна быть абсолютно интегрируема, т.е. должен существовать интеграл Функция должна иметь
- 20. Основные свойства преобразования Фурье 1. Взаимная однозначность 2. Линейность 3. Теорема смещения
- 21. Основные свойства преобразования Фурье 4. Теорема о свертке Прямая теорема: преобразование Фурье от свертки двух функций
- 22. Основные свойства преобразования Фурье 5. Теорема Парсеваля для интеграла Фурье Равенство Парсеваля
- 23. Основные свойства преобразования Фурье 6. Дельта-функция и функция Хевисайда Дельта-функция Функция Хевисайда (ступенька)
- 24. Теорема отсчетов 1935 г. В.А. Котельников; 1945 г. Клод Шенон; 1915 г. Уиттекер Функция с ограниченным
- 25. Доказательство теоремы отсчетов доопределили функцию как периодическую применили обратное преобразование Фурье применили обратную теорему о свертке
- 26. Доказательство теоремы отсчетов. Ряд Котельникова. Число степеней свободы функции Ряд Котельникова позволяет вычислить с любой точностью
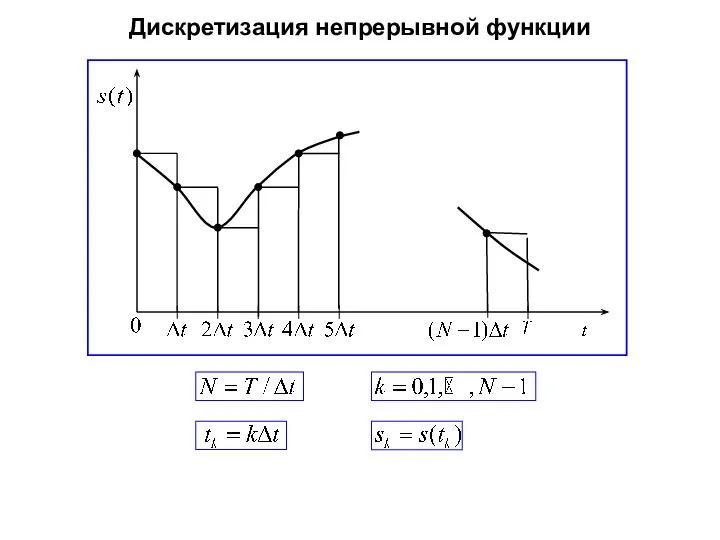
- 27. Дискретизация непрерывной функции
- 28. Численный спектральный анализ Получить самостоятельно выражения для численного расчета интегралов, применив левостороннюю формулу прямоугольников В окончательную
- 29. Численный спектральный анализ интегральная сумма по левосторонней формуле прямоугольников формулы для численного расчета коэффициентов Фурье
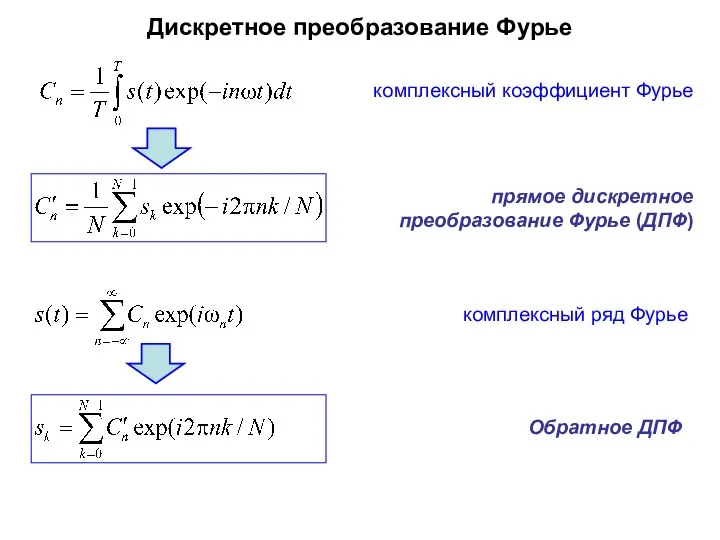
- 30. Дискретное преобразование Фурье комплексный коэффициент Фурье прямое дискретное преобразование Фурье (ДПФ) Обратное ДПФ комплексный ряд Фурье
- 31. Свойства ДПФ Линейность Число коэффициентов ДПФ равно числу N элементов исходной последовательности Постоянная составляющая (коэффициент с
- 32. Если - дискретная последовательность вещественных чисел, то имеет место равенство Свойства ДПФ комплексное сопряжение
- 33. Если - дискретная последовательность вещественных чисел, то имеет место равенство поэтому можно считать, что вторая половина
- 34. Периодическое продолжение дискретной последовательности Свойства ДПФ обратное ДПФ
- 35. Частоты ДПФ положительные частоты отрицательные частоты максимальная частота Пусть последовательность из отсчетов является дискретным представлением непрерывной
- 36. Пример с перестановкой частот комплексного спектра ДПФ
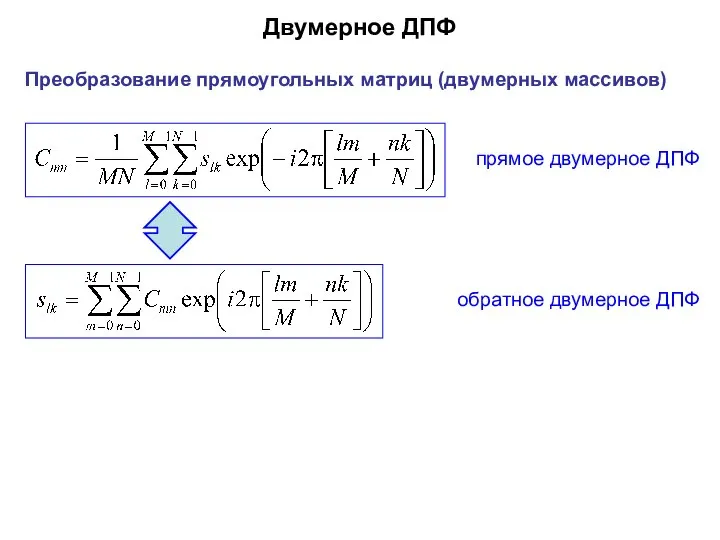
- 37. Двумерное ДПФ прямое двумерное ДПФ обратное двумерное ДПФ Преобразование прямоугольных матриц (двумерных массивов)
- 38. Быстрое преобразование Фурье Быстрое преобразование Фурье (БПФ) - “быстрый” алгоритм расчета ДПФ
- 39. Быстрое преобразование Фурье
- 40. Быстрое преобразование Фурье Порядок сложности алгоритма БПФ Порядок сложности алгоритма ДПФ
- 41. Cредства Mathcad для реализации ДПФ и БПФ Встроенные функции (пары функций) – см. описания в справочной
- 42. Сходимость ряда Фурье Пусть s(t) – кусочно непрерывно дифференцируемая функция с периодом T. Тогда ряд Фурье
- 43. Скорость сходимости ряда Фурье Скорость сходимости ряда Фурье функции s(t) зависит от ее гладкости - количества
- 44. Эффект Гиббса Явление Гиббса: неравномерная сходимость ряда Фурье функции s(t) с периодом T в точках разрыва.
- 45. Эффект Гиббса. Пример
- 46. Сглаживание пульсаций. Сигма-факторы Методика сглаживания К. Ланцоша – усреднение частичных сумм ряда Фурье по периоду последнего
- 47. Сглаживание пульсаций. Сигма-факторы Методика сглаживания К. Ланцоша – усреднение частичных сумм ряда Фурье по периоду последнего
- 49. Скачать презентацию











































 Математическое путешествие по сказке (для дошкольников)
Математическое путешествие по сказке (для дошкольников) Кратные и двойные интегралы
Кратные и двойные интегралы Презентация по математике "Страна "Геометрия"" - скачать
Презентация по математике "Страна "Геометрия"" - скачать  Ожившие задачи и теоремы
Ожившие задачи и теоремы Определение автокорреляции
Определение автокорреляции Теорема синусов и косинусов
Теорема синусов и косинусов Математические основы манипулирования реляционными данными
Математические основы манипулирования реляционными данными Внеклассное мероприятие по математике в 9 классе Весёлая экономика
Внеклассное мероприятие по математике в 9 классе Весёлая экономика Правильные и неправильные дроби 5 класс - Презентация
Правильные и неправильные дроби 5 класс - Презентация Деление чисел
Деление чисел Музей математики Зал 1. Галерея математиков
Музей математики Зал 1. Галерея математиков Математические загадки
Математические загадки Сложение и вычитание многочленов
Сложение и вычитание многочленов Пропорции и отношения. Урок – игра «Математическая поликлиника» 6 класс
Пропорции и отношения. Урок – игра «Математическая поликлиника» 6 класс Бинарные операции над нечёткими множествами
Бинарные операции над нечёткими множествами ПРОБЛЕМЫ СИСТЕМАТИЧЕСКИХ И СЛУЧАЙНЫХ ОШИБОК
ПРОБЛЕМЫ СИСТЕМАТИЧЕСКИХ И СЛУЧАЙНЫХ ОШИБОК  Прямоугольный параллелепипед
Прямоугольный параллелепипед Стандартные измерения геометрических величин
Стандартные измерения геометрических величин Биология и математика в огненные годы ВОВ
Биология и математика в огненные годы ВОВ Техника формирования граф логических структур
Техника формирования граф логических структур Измерение углов транспортиром
Измерение углов транспортиром Ознаки предметів
Ознаки предметів Ось симметрии. 5 класс
Ось симметрии. 5 класс Признаки делимости на 11
Признаки делимости на 11 Многогранники вокруг нас (11 класс) - презентация_
Многогранники вокруг нас (11 класс) - презентация_ Алгебралық Салу есептери. Алгебралық және инверсия әдiсi
Алгебралық Салу есептери. Алгебралық және инверсия әдiсi Соединения с повторениями
Соединения с повторениями Презентация по математике "Математика 4 класс «Деление»" - скачать бесплатно
Презентация по математике "Математика 4 класс «Деление»" - скачать бесплатно