Содержание
- 2. Формулы для вычисления интеграла получают следующим образом. Интервал [a, b] разбивают на n отрезков длиной h
- 3. Интерполяционным многочленом называ-ют алгебраический многочлен степени (n – 1), со-впадающий с аппроксимируемой (заменяемой) функцией в выбранных
- 4. В результате получают выражение интеграла (формулу численного интегрирования) через зна-чения подынтегральной функции в выбранной системе точек.
- 5. Формула средних Формула средних получается, если на каж-дом i-м отрезке взять один центральный узел xi+1/2 =
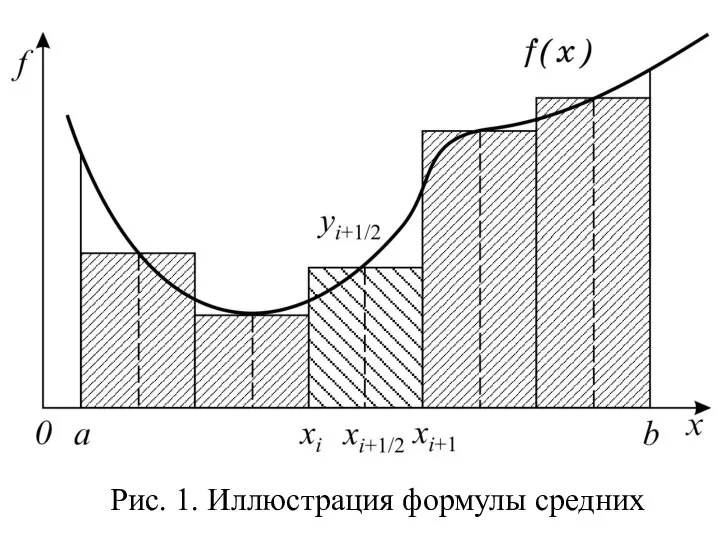
- 6. Рис. 1. Иллюстрация формулы средних
- 7. Формула трапеций Формула трапеций получается при замене функции f(x) на каждом отрезке [xi, xi+1] многочленом первого
- 8. Рис. 2. Иллюстрация формулы трапеций
- 9. Формула Симпсона Эта формула получается при замене функции f(x) на каждом отрезке [xi, xi+1] многочленом второго
- 10. После приведения подобных членов полу-чаем более удобный для программирования вид:
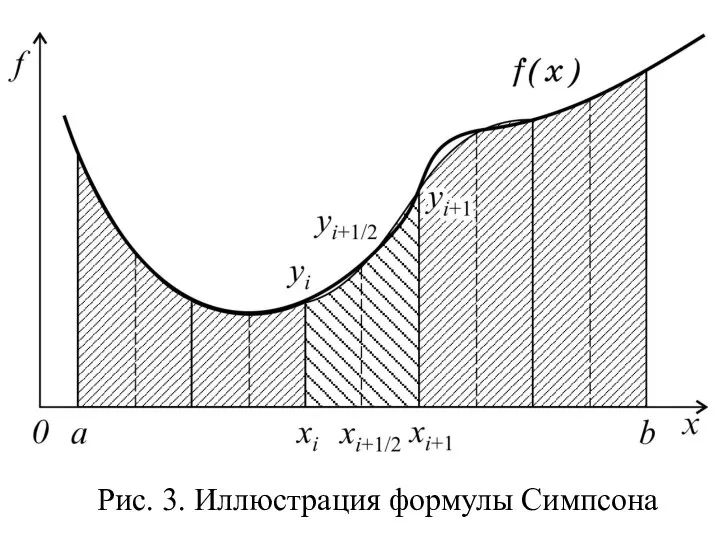
- 11. Рис. 3. Иллюстрация формулы Симпсона
- 12. Расчет интеграла по заданной точности ε Метод 1. Один из вариантов вычисления интеграла с заданной точностью:
- 13. Метод 2 – классическая схема автоматиче-ского выбора шага. Анализ формул (1) – (3) показал, что точное
- 14. Формулы Гаусса В рассмотренных формулах в качестве узлов многочлена выбирались середины и (или) концы интервала разбиения.
- 15. Анализ показал, что узлами, удовлетворяю-щими такому условию, являются нули ортого-нальнoго многочлена Лежандра степени n : {
- 16. Для n = 2 узлы должны быть выбраны сле-дующим образом (два узла): xi1 = xi+1/2 –
- 17. Для n = 3 выбираются три узла: xi0 = xi+1/2 ; xi1 = xi0 – h/2
- 18. Рассмотрим пример Написать и отладить программу вычисления значения интеграла от функции f(x) = 4 x –
- 19. void main () { double a, b, x, eps, h, I1, I2, pogr; int n, n1,
- 20. if ( kod == 1 ) { // Выполняем расчет по числу разбиений n cout cin
- 21. do { /* Увеличиваем число разбиений и находим новое значение интеграла I2 */ n1 *= 2;
- 22. cout /* Выводим количество разбиений n1, при кото-ром была достигнута заданная точность */ } // Конец
- 23. Функция метода Симпсона double Metod (double ( *f ) (double x), double a, double b, int
- 25. Скачать презентацию
![Формулы для вычисления интеграла получают следующим образом. Интервал [a, b] разбивают](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/675507/slide-1.jpg)



















 Приёмы устных вычислений вида: 470+80, 560-90
Приёмы устных вычислений вида: 470+80, 560-90 Добери знак
Добери знак Противоположные числа Какие числа называют противоположными? Как на координатной прямой располагаются точки, соответствующие п
Противоположные числа Какие числа называют противоположными? Как на координатной прямой располагаются точки, соответствующие п Элементы теории вероятностей
Элементы теории вероятностей Длина окружности. Коллекция задач для 6 класса
Длина окружности. Коллекция задач для 6 класса Матриці та дії над ними. Поняття і види матриць
Матриці та дії над ними. Поняття і види матриць Первообразная и неопределённый интеграл
Первообразная и неопределённый интеграл Свойства двойного интеграла
Свойства двойного интеграла Дифференциал функции
Дифференциал функции Метрология. Основные понятия
Метрология. Основные понятия Правильные многоугольники
Правильные многоугольники Арифметическая и геометрическая прогрессии Учитель математики МБОУ «Адаевская ООШ» Актанышского муниципального района Респу
Арифметическая и геометрическая прогрессии Учитель математики МБОУ «Адаевская ООШ» Актанышского муниципального района Респу Презентация по математике "Теорема Пифагора" -
Презентация по математике "Теорема Пифагора" -  Многогранники. Все формулы. Геометрия (10-11 класс)
Многогранники. Все формулы. Геометрия (10-11 класс) Математическое моделирование. Значимость коэффициентов регрессии
Математическое моделирование. Значимость коэффициентов регрессии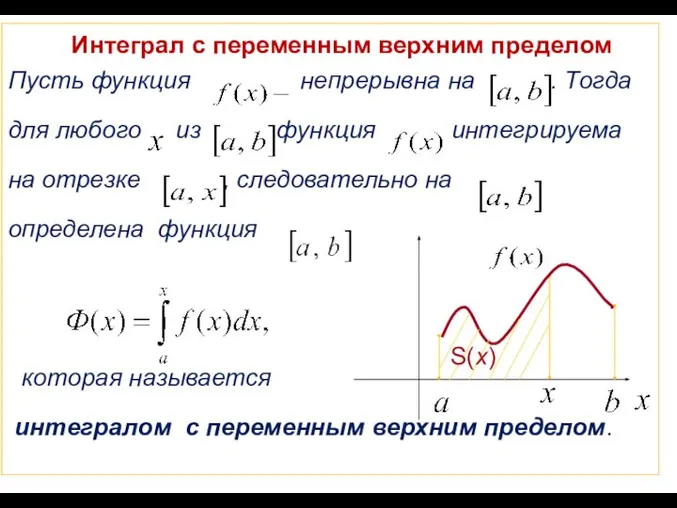 Интеграл с переменным верхним пределом
Интеграл с переменным верхним пределом Количественные характеристики случайной величины. Описательная статистика. (Лекция 4)
Количественные характеристики случайной величины. Описательная статистика. (Лекция 4) Математические забавы
Математические забавы Построение информационной модели метода изготовления изделия
Построение информационной модели метода изготовления изделия Применение подобия к доказательству теорем и решению задач. Урок 38
Применение подобия к доказательству теорем и решению задач. Урок 38 Площа бічної та повної поверхонь конуса
Площа бічної та повної поверхонь конуса Математика вокруг нас. Внеклассное мероприятие
Математика вокруг нас. Внеклассное мероприятие Презентация по математике "Упрощение выражений 6 класс" - скачать
Презентация по математике "Упрощение выражений 6 класс" - скачать  Практикум по решению задачи №20 (базовый уровень). ЕГЭ
Практикум по решению задачи №20 (базовый уровень). ЕГЭ Размещение из N элементов по k (k ≤ n)
Размещение из N элементов по k (k ≤ n) Число 14. Многоугольники
Число 14. Многоугольники Иррациональные неравенства. Виды и способы решения
Иррациональные неравенства. Виды и способы решения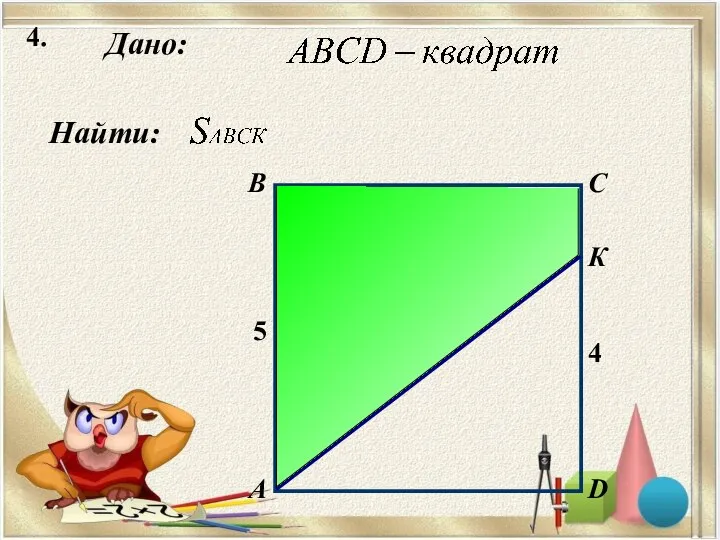 Решение задач на площадь треугольника
Решение задач на площадь треугольника