Содержание
- 3. Элементы булевой алгебры Основными элементами булевой алгебры являются: Логические константы В булевой алгебре определены две логические
- 4. Переменные Булевы (логические, двоичные) переменные - переменные, принимающие значения из множества {0,1}. Операция отрицания является унарной,
- 5. Операции обозначаются следующим образом: Выражения Логическим (булевым) выражением называется совокупность булевых переменных, соединенных знаками булевых операций
- 6. Примеры логических выражений: . Областью определения булевой функции является совокупность 2n двоичных наборов ее аргументов. Набор
- 7. Булеву функцию можно задать с помощью следующих форм: Аналитическая форма – булева функция задается логическим выражением,
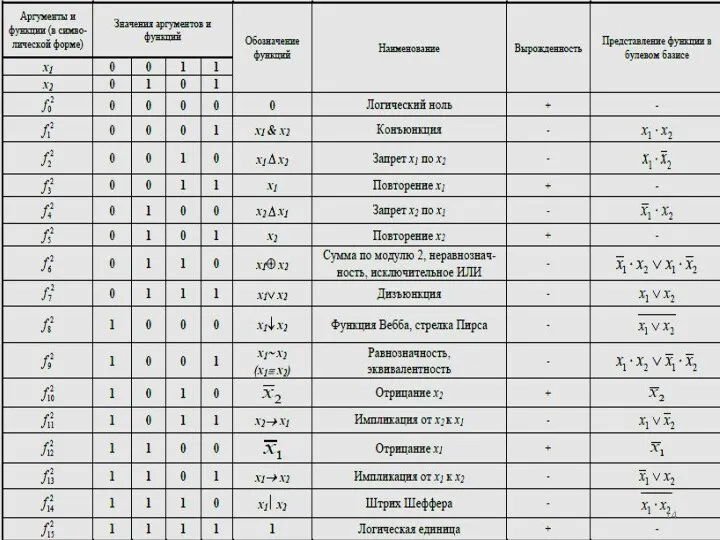
- 8. Табличная форма – булева функция задается таблицей истинности. Переход от аналитической формы к табличной однозначен. Обратный
- 9. Остальные формы задания булевой функции рассматриваются в следующих разделах.
- 10. Коммутативные (переместительные) законы: 2. Ассоциативные (сочетательные) законы: 7. Законы единичного элемента: Основные законы булевой алгебры К
- 11. 8. Законы дополнительного элемента. В булевой алгебре дополнительным элементом по отношению к а является отрицание Большинство
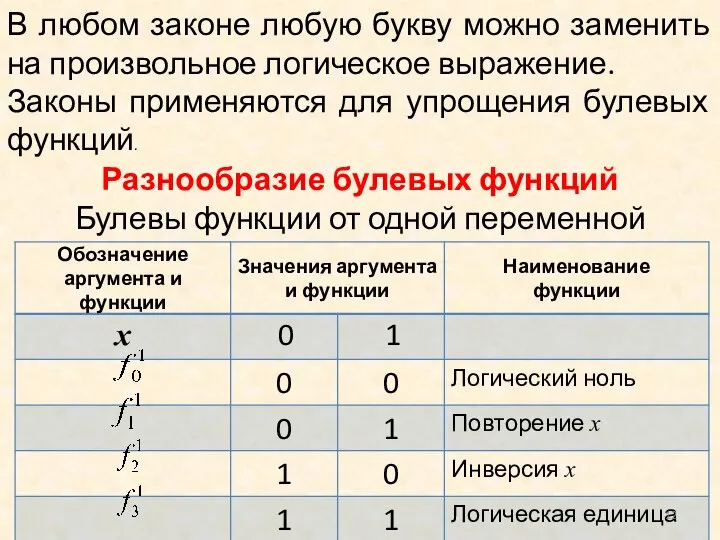
- 12. В любом законе любую букву можно заменить на произвольное логическое выражение. Законы применяются для упрощения булевых
- 13. Булева функция от n аргументов fn(Х) называется вырожденной по аргументу xi, если ее значение не зависит
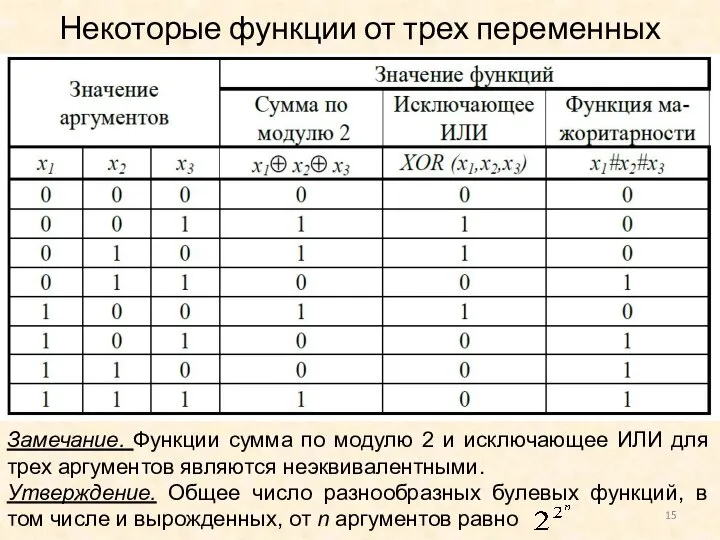
- 15. Некоторые функции от трех переменных Замечание. Функции сумма по модулю 2 и исключающее ИЛИ для трех
- 16. Нормальные формы булевых функций Нормальные формы - это особый класс аналитических выражений, используемых при решении задачи
- 17. Под буквой будем понимать аргумент булевой функции или его отрицание. Примерами термов являются: Выражения типа: термами
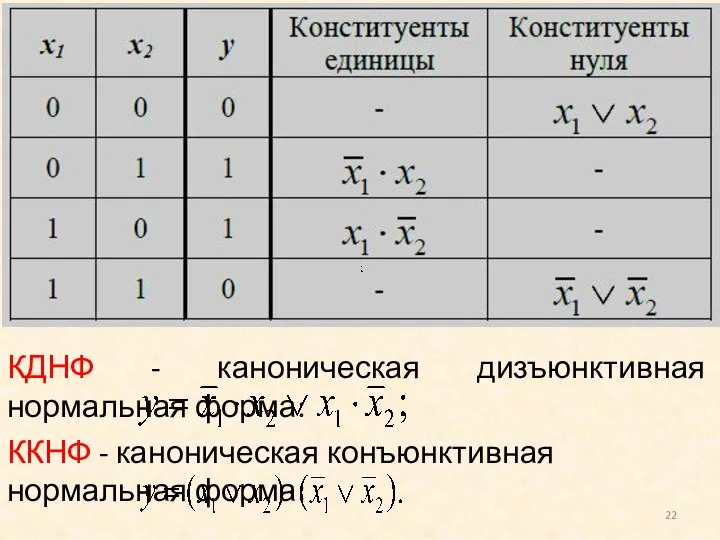
- 18. Конституентой единицы (нуля) называется конъюнктивный (дизъюнктивный) терм макси-мального ранга, т.е. для булевой функции от n переменных
- 19. Определение. Дизъюнктивная (конъюнктивная) нормальная форма называется канонической, если все ее конъюнктивные (дизъюнктивные) термы представляют собой конституенты
- 20. 3. Любая булева функция, за исключением логического нуля и логической единицы, имеет единственные КДНФ и ККНФ.
- 21. в) объединением конституенты единицы (нуля) знаками дизъюнкции (конъюнкции) получается аналитическая форма в виде КДНФ (ККНФ). Пояснение.
- 22. КДНФ - каноническая дизъюнктивная нормальная форма: ККНФ - каноническая конъюнктивная нормальная форма:
- 23. КДНФ и ККНФ представляют собой две различные, но эквивалентные аналитические формы булевой функции. Это означает, что
- 24. Числовая и символическая формы представления булевых функций Для любой булевой функции можно предложить две числовые формы,
- 25. Пример. Функция от трех переменных задана в числовой форме: От числовой формы легко перейти к КДНФ
- 26. В самом компактном виде любую булеву функцию можно представить в следующей символической форме: где n-количество аргументов,
- 27. Пример. f3(Х)=x1⊕x2⊕x3 (01101001)2 = 64 + 32 + 8 + 1 = 105 f3(Х)=x1⊕x2⊕x3 = -
- 28. Преобразование произвольной аналити-ческой формы булевой функции в нормальную В булевой алгебре в виде теоремы доказывается следующее
- 29. 1. В общем случае любая булева функция может иметь несколько ДНФ, отличающихся либо количеством термов, либо
- 30. 3. По сравнению со схемой, построенной по ДНФ, схема, построенная по скобочной форме (*), является предпочтительной
- 31. в) раскрытие скобок с применением дистрибу-тивного закона; Приведение произвольных нормальных форм булевой функции к каноническим Для
- 32. где P - неполный конъюнктивный терм (ранг этого терма меньше n), а xi - недостающий в
- 33. Замечание. После раскрытия скобок могут получиться одинаковые термы, из которых нужно оставить только один. - числовая
- 34. - числовая форма функции.
- 35. Разнообразие двоичных алгебр В связи с тем, что любую сколь угодно сложную булеву функцию можно представить
- 36. К наиболее распространенным двоичным алгебрам относятся: алгебра Жегалкина (⊕, &); алгебра Вебба (Пирса) (↓); алгебра Шеффера
- 37. Кубическое представление булевых функций В кубическом представлении булевой функции от n переменных все множество из 2n
- 38. Пример. Для функции f 4(X) определить, являются ли ее 0-кубы (0101) и (0001) соседними и, если
- 39. Пример. Для функции f 4(X) определить, являются ли ее 1-кубы (0Х01) и (0Х11) соседними и, если
- 40. Замечания. Размерность куба определяется количеством свободных координат. 2. В соседних r-кубах (r > 0) все свободные
- 41. Аналогично, для другого примера 1-кубу (0Х01) соответствует терм , а 1-кубу (0Х11) – терм Эти термы
- 42. Пример. Получить кубический комплекс функции Для получения кубического комплекса K(f) необ-ходимо провести всевозможные операции склеи-вания над
- 43. Пояснения. Получение 1-кубов осуществляется на основе попарного сравнения 0-кубов с целью выявления всевозможных пар соседних 0-кубов
- 44. Замечания. Для данного примера в записи 0-кубов в кубическом комплексе K0(f) в порядке возрастания их десятичных
- 45. При склеивании 1-кубов 2-кубы представлены в двух экземплярах как результаты склеивания двух различных пар 1-кубов. Распространяя
- 46. Графическое представление булевых функций. Геометрическая интерпретация кубов малой размерности Графическое представление булевых функций носит ограниченный характер
- 47. Таким образом, множество наборов аргументов булевой функции, представляющих область ее определения, можно отождествить с множеством вершин
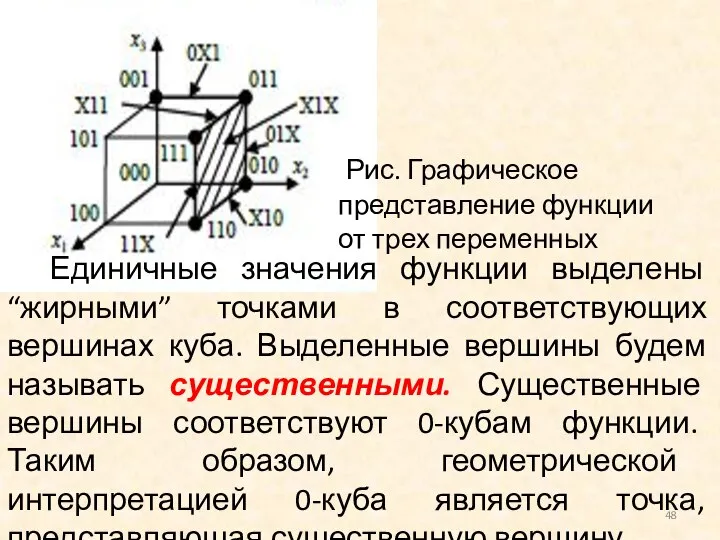
- 48. Рис. Графическое представление функции от трех переменных Единичные значения функции выделены “жирными” точками в соответствующих вершинах
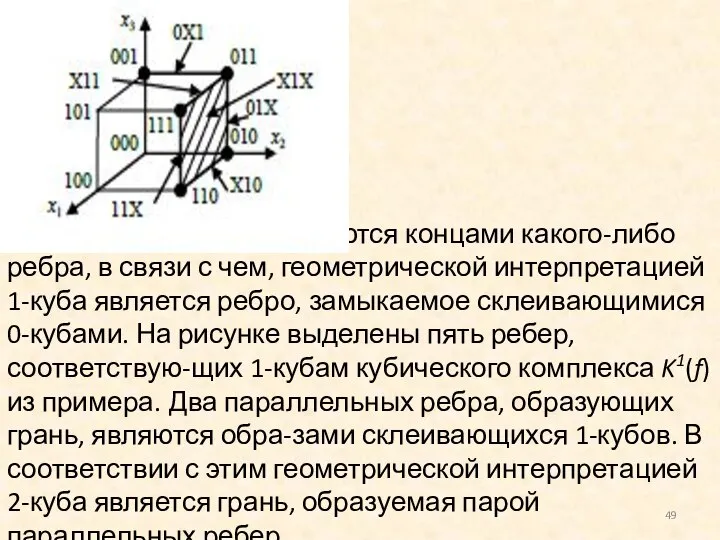
- 49. Два соседних 0-куба являются концами какого-либо ребра, в связи с чем, геометрической интерпретацией 1-куба является ребро,
- 50. Так как любую грань можно определить одной из пар параллельных ребер, 2-куб может быть получен как
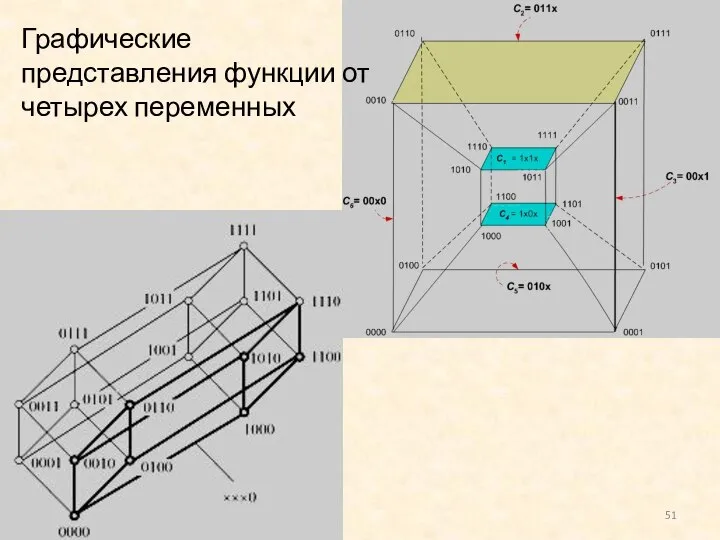
- 51. Графические представления функции от четырех переменных
- 52. Задача минимизации булевых функций и методы ее решения Аналитические выражения булевых функций являются математическими моделями, на
- 53. Если в схеме используются элементы k типов с ценами s1, s2, ..., sk и в количестве
- 54. Канонический метод проектирования комбина-ционных схем состоит в следующем. Закон функционирования проектируемой схемы, в общем случае, задается
- 55. Замечание. Для схем с так называемыми парафазными входами (на входы схемы подаются как прямые, так и
- 56. Использование SQ в качестве критерия оптималь-ности синтезируемой схемы предполагает, что схема должна строится по аналитическому выражению
- 57. Методы минимизации булевых функций Методы решения задачи минимизации булевых функций можно разделить на две группы: графические
- 58. Решение задачи минимизации сводится к нахождению минимального покрытия булевой функции. Основными достоинствами графического метода минимизации булевых
- 59. Большим недостатком графического метода мини-мизации является также отсутствие формализо-ванного подхода к решению задачи (метод явля-ется во
- 60. Покрытия булевых функций Построение покрытий булевых функций из кубов различной размерности. Соответствие между покрытием и ДНФ
- 61. Отношение включения (покрытия) между кубами обозначается: А ⊂ B. Для примера отношения включения имеют место между
- 62. Покрытием булевой функции f называется такое подмножество кубов из кубического комплекса K(f), которое покрывает все существенные
- 63. Этому покрытию соответствует ДНФ вида: которая не является минимальной. В качестве еще одного варианта покрытия можно
- 64. Действительно, кубы, входящие в Z(f), покрывают все существенные вершины: 0Х1⊃(001, 011), Х1Х⊃(010, 011, 110, 111). Эта
- 65. Покрытие булевой функции, которое соответствует минимальной ДНФ, называется минимальным покрытием и обозначается Сmin (f). Замечание: Минимальное
- 66. Пример. Минимизируемая булева функция задана в числовой форме: Найти ее минимальное покрытие и МДНФ. По числовой
- 67. Все 0-кубы функции вступили хотя бы в одну операцию склеивания и, следовательно, среди них нет максимальных.
- 68. Из анализа покрытия существенных вершин максимальными кубами из комплекса K1(f) следует: 1. Куб (00Х) должен обязательно
- 69. Для ее покрытия достаточно взять любой из оставшихся максимальных кубов: (Х00) или (1Х0). Таким образом, для
- 70. Выводы: 1. Задача получения минимальной ДНФ сводится к задаче получения минимального покрытия булевой функции. 2. В
- 71. 3. Частными случаями могут являться: Cmin(f) = K0(f). Минимальное покрытие совпадает с кубическим комплексом K0(f). При
- 72. б) T(f) ⊂ Cmin(f). Минимальное покрытие включает в себя ядро, как обязательную часть, и дополняется минимальным
- 73. Цена покрытия Цена покрытия используется при решении задачи минимизации булевых функций как коли-чественная оценка качества покрытия
- 74. где k – общее количество кубов, входящих в покрытие. Минимальным покрытием булевой функции называется покрытие, обладающее
- 75. Пример. Определить цены покрытий функции C0(f)=K0(f): Sa=5⋅3=15; Sb=Sa+5=20; C1(f)=K1(f): Sa=4⋅2=8; Sb=Sa+4=12; C2(f)=Cmin(f): Sa=3⋅2=6 ; Sb=9.
- 76. Цены покрытия Sa и Sb связаны с ДНФ, соответствующей этому покрытию, следующим образом: - цена покрытия
- 77. Пример. Построить логическую схему, реализующую булеву функцию по МДНФ из примера. Определить цену схемы по Квайну
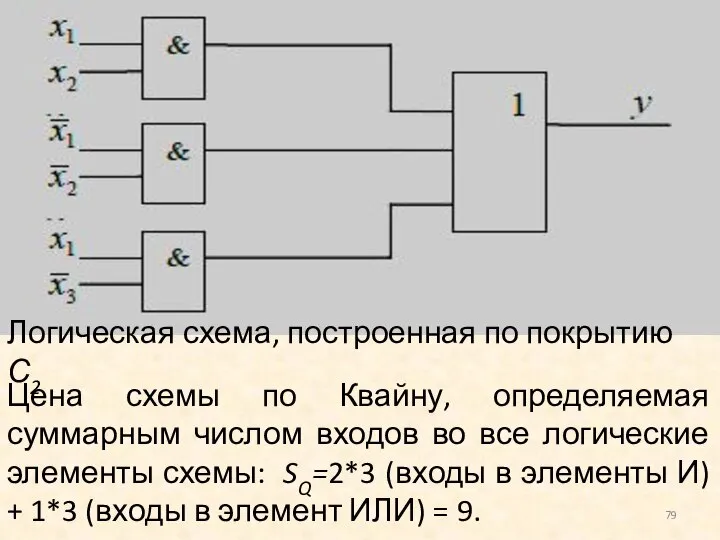
- 78. Для интерпретации выражения для МДНФ в схему представим его в следующем виде: И(2) И(2) И(2) ИЛИ(3)
- 79. Логическая схема, построенная по покрытию С2 Цена схемы по Квайну, определяемая суммарным числом входов во все
- 80. В свою очередь, цены покрытия по МДНФ, по которой строилась схема, Sa =6, Sb =9. Таким
- 81. Нулевое покрытие булевой функции и получение МКНФ Выше было рассмотрено покрытие булевой функции на наборах аргументов,
- 82. Пример. Для булевой функции найти минимальное нулевое покрытие и составить МКНФ. Альтернативное числовое представление булевой функции
- 83. Sa=9 Sb=12; в результате чего получим кубический комплекс Поскольку 0-куб (101) не склеивался с другими 0-кубами,
- 84. Минимальное нулевое покрытие совпадает с множеством максимальных кубов: Замечания. Для того, чтобы отличать нулевое покрытие от
- 85. Минимизация булевых функций на картах Карно Одним из способов графического представления булевых функций от небольшого числа
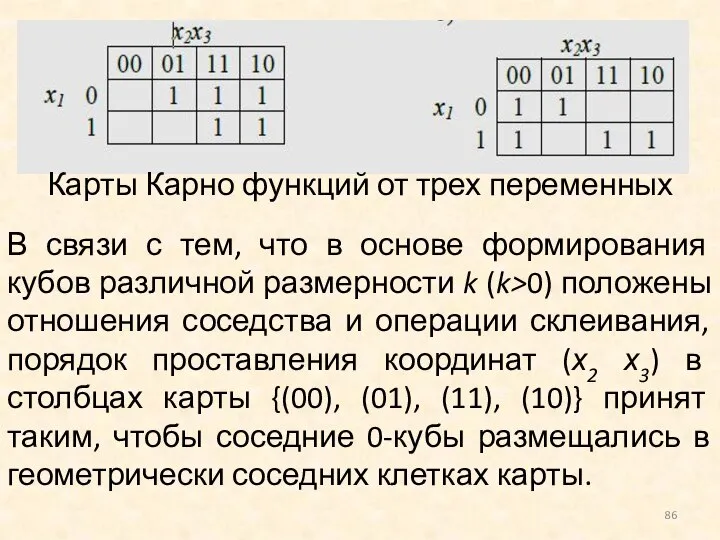
- 86. Карты Карно функций от трех переменных В связи с тем, что в основе формирования кубов различной
- 87. Пример карты Карно для булевой функции от четырех переменных, заданной в числовой форме: С использованием карт
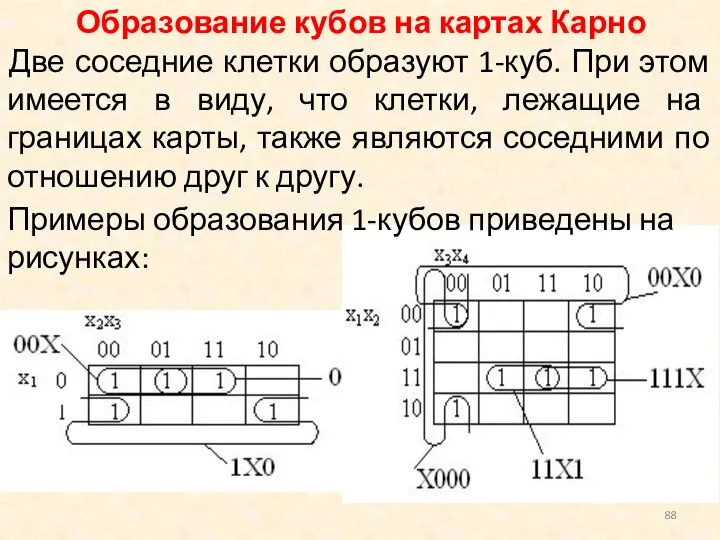
- 88. Образование кубов на картах Карно Две соседние клетки образуют 1-куб. При этом имеется в виду, что
- 89. Карты позволяют для функций f1 и f2, заданных комплексами K0(f1) и K0(f2) с ценами Sа(f1) =
- 90. Эти покрытия являются минимальными и им соответствуют минимальные ДНФ: Четыре клетки карты могут объединяться, образуя 2-куб,
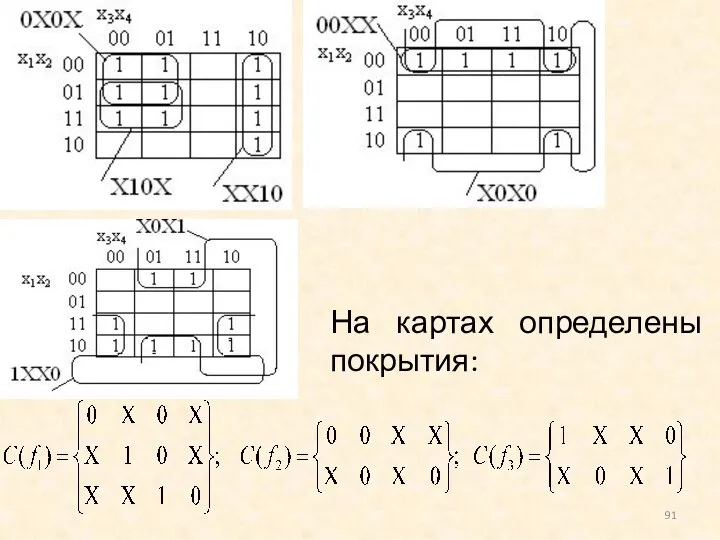
- 91. На картах определены покрытия:
- 92. имеющие цены Sa(f1) = 6, Sb(f1) = 9, Sa(f2) = 4, Sb(f2) = 6, Sa(f3) =
- 93. Функциям f1, f2, f3 соответствуют покрытия с одинаковыми ценами Sа = 2, Sb = 4.
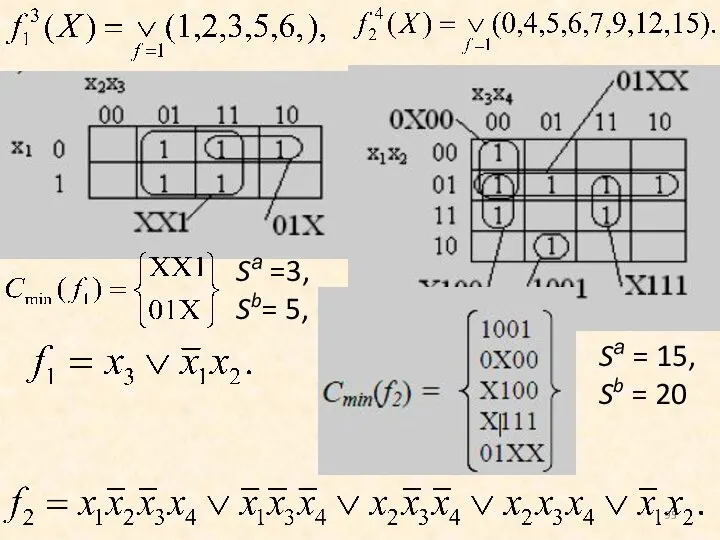
- 94. Определение минимальных покрытий и МДНФ Для получения минимальной ДНФ функции с использованием карты Карно определяется покрытие
- 95. Sа =3, Sb= 5, Sа = 15, Sb = 20
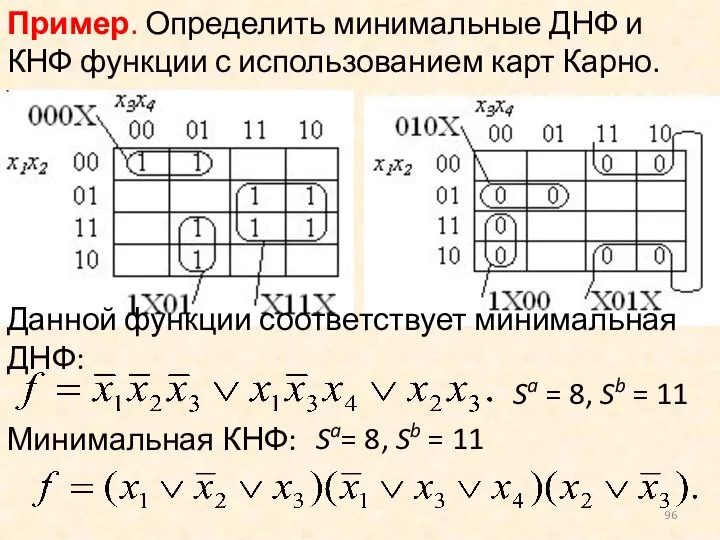
- 96. Данной функции соответствует минимальная ДНФ: Минимальная КНФ: Sa = 8, Sb = 11 Sa= 8, Sb
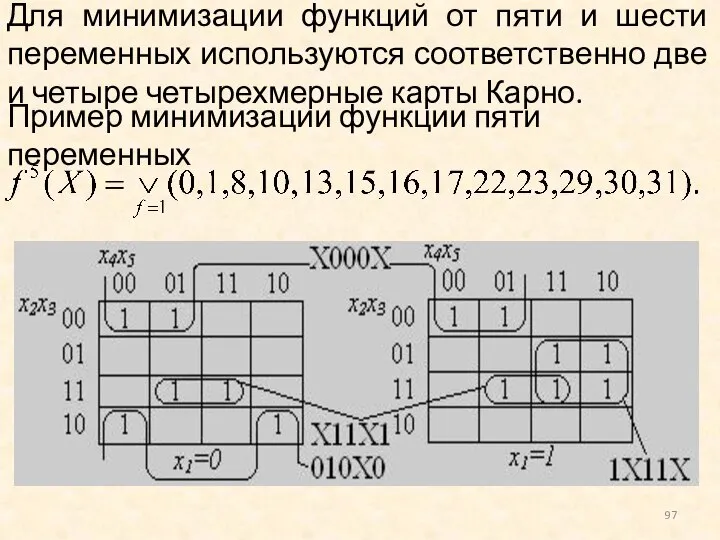
- 97. Для минимизации функций от пяти и шести переменных используются соответственно две и четыре четырехмерные карты Карно.
- 98. Минимальное покрытие функции: имеет цены Sа = 13, Sb = 17. Ему соответствует МДНФ: Разделение четырехмерных
- 99. в соседней карте и имеет в ней одинаковые с исходной клеткой координаты х2, х3, х4, х5,
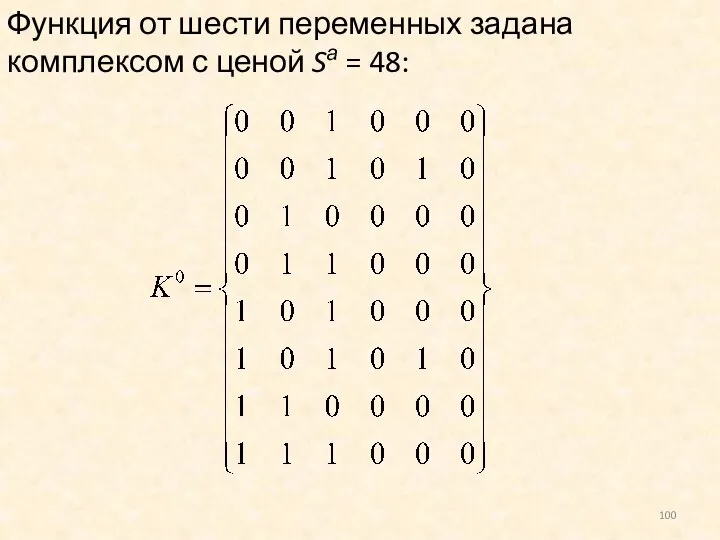
- 100. Функция от шести переменных задана комплексом с ценой Sа = 48:
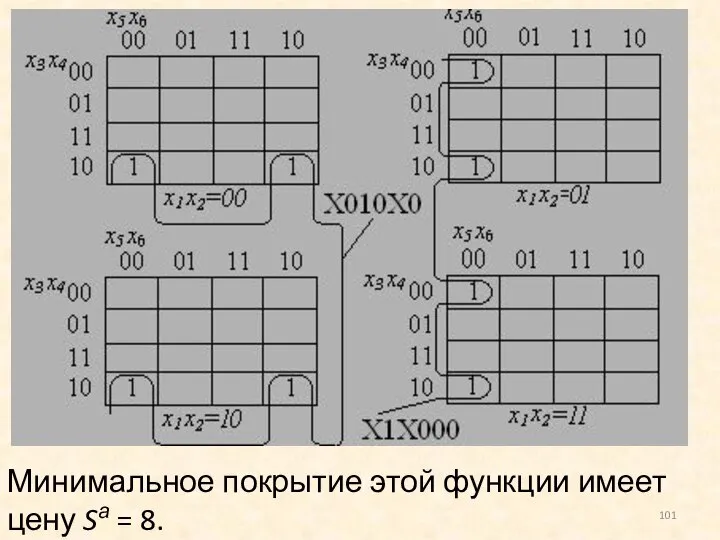
- 101. Минимальное покрытие этой функции имеет цену Sа = 8.
- 102. При минимизации функций от большого числа переменных карты Карно неудобны, в этом случае для решения задач
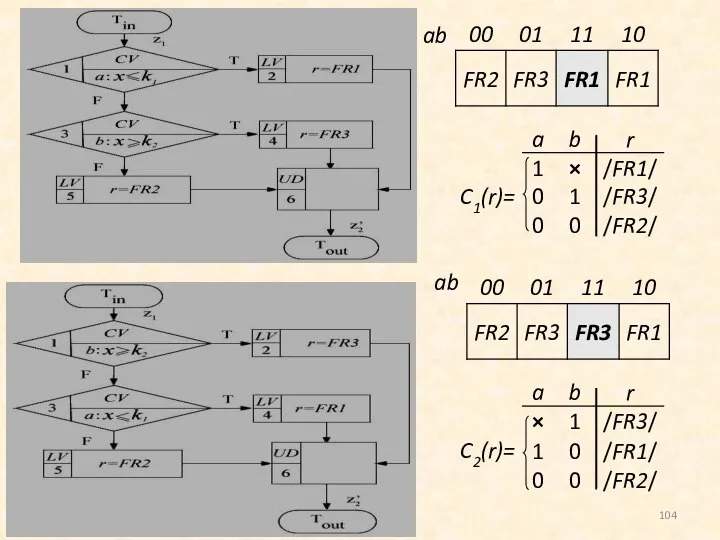
- 103. Пример. Пусть задана интервальная формула, вычисляющая значение некоторой переменной r от значения переменной x, Введем булевы
- 104. ab ab
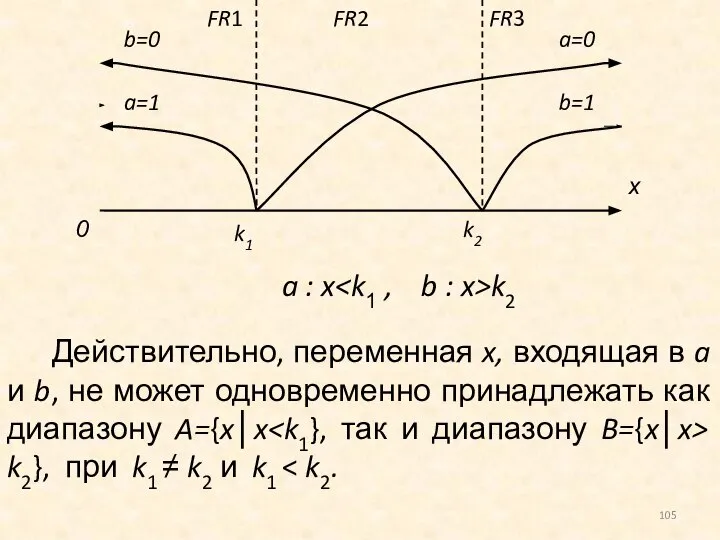
- 105. a : x Действительно, переменная x, входящая в a и b, не может одновременно принадлежать как
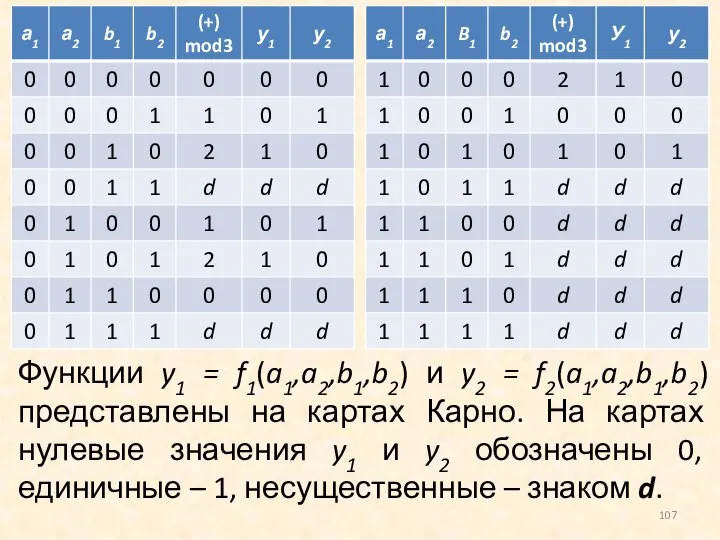
- 106. Пример. Найти минимальную ДНФ функций, используемых для построения комбинационной схемы, в которой выполняется операция суммирования двоичных
- 107. Функции y1 = f1(a1,a2,b1,b2) и y2 = f2(a1,a2,b1,b2) представлены на картах Карно. На картах нулевые значения
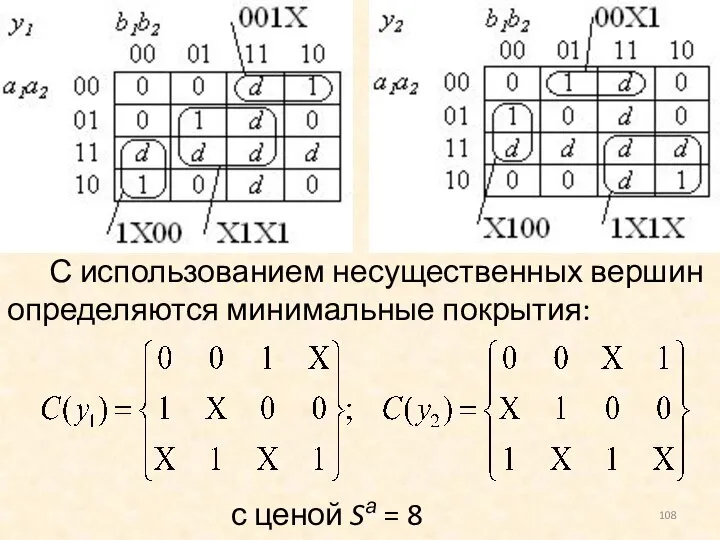
- 108. С использованием несущественных вершин определяются минимальные покрытия: с ценой Sа = 8 каждое.
- 109. Покрытиям соответствуют минимальные ДНФ: Замечание. После минимизации функция становится полностью определенной. Значения функции на несущественных наборах
- 110. Импликанты булевой функции. Системы импликант Решение задачи минимизации булевой функции методом Квайна и усовершенствованным методом Квайна-Мак-Класки
- 111. 2. Можно утверждать, что для любого набора аргументов, на котором функция равна нулю, ее импликанта также
- 112. Т.е. произвольная дизъюнкция этих термов также является импликантой функции. Простой (первичной) импликантой булевой функции называется конъюнктивный
- 113. Множеству простых импликант можно поставить в соответствие множество максимальных кубов. Понятие «сокращенная» присвоено ДНФ в том
- 114. Аналогия между импликантами и кубическим представлением булевой функции Любому кубу из К(f) можно поставить в соответ-ствие
- 115. В отношении импликант булевой функции также как и в отношении кубов, соответствующих им, существует отношение покрытия.
- 116. Наример, импликанта х1х2 покрывает сущест-венные вершины (110, 111) и в свою очередь покрывает куб 11Х. Множество
- 117. Так, например, кубам из кубического комплекса К° (f) соответствует полная система импликант, представляющая собой множество конституент
- 118. Пример. Проверить, является ли система простых импликант для функции полной и, если да, то является ли
- 119. Для функции примера существуют две ТДНФ: 1. 2. В данном случае они совпадают с минимальной ДНФ.
- 120. Минимизация булевых функций методом Квайна-Мак-Класки 3. Дополнение множества кубов, принадлежащих ядру покрытия, минимальным подмножеством из множества
- 121. С точки зрения последовательного преобразова-ния ДНФ булевой функции с целью их упрощения каноническая задача минимизации может
- 122. Пример. Минимизация булевой функции методом Квайна-Мак-Класки. Найти множество простых импликант булевой функции заданной в числовой форме:
- 123. При таком подходе в операцию склеивания могут вступать только кубы, принадлежащие двум сосед-ним группам, то есть
- 124. Результат этого этапа представлен в таблице
- 125. Замечания. При образовании 2-кубов получено два одинаковых 2-куба как результата склеивания двух различных пар соседних 1-кубов.
- 126. Определение ядра покрытия Для выполнения этого этапа первоначально строится таблица покрытий, строки которой соответствуют мак-симальным кубам
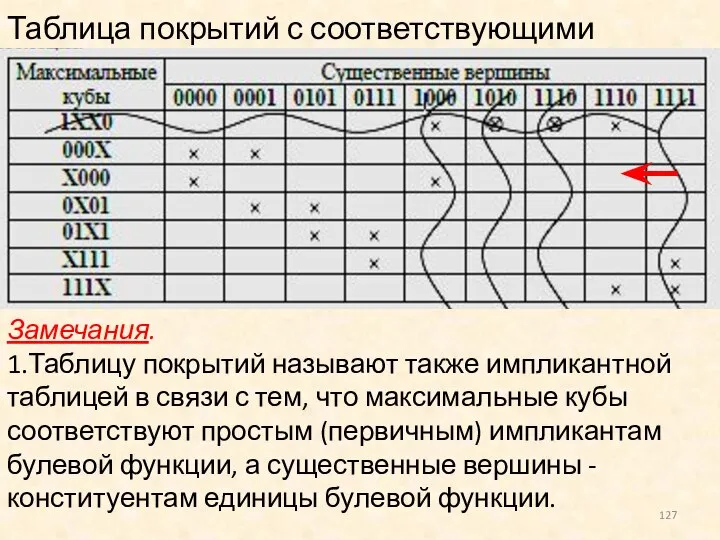
- 127. Таблица покрытий с соответствующими отметками Замечания. 1.Таблицу покрытий называют также импликантной таблицей в связи с тем,
- 128. 2. Для полностью определенных булевых функций количество меток в строке таблицы покрытий, соответствующей максимальному кубу размерности
- 129. Как видно из таблицы, в нашем примере кубом ядра будет являться куб: T(f)={1ХХ0}. Определение множества минимальных
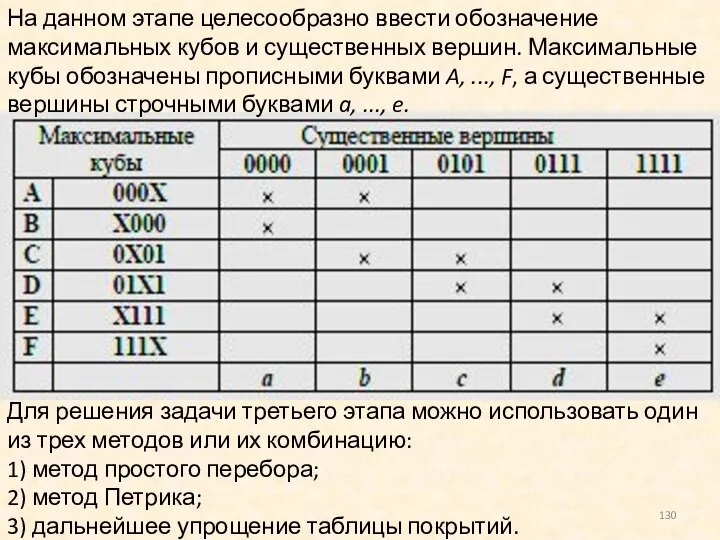
- 130. Для решения задачи третьего этапа можно использовать один из трех методов или их комбинацию: 1) метод
- 131. Метод перебора целесообразно применять для упро-щенной таблицы небольшого объема. Он не дает гаран-тии получения всех максимальных
- 132. Метод Петрика основан на составлении булева выраже-ния, определяющего условие покрытия всех существен-ных вершин булевой функции из
- 133. Для рассматриваемого примера булево выражение, опре-деляющее условие покрытия всех существенных вершин в соответствии с таблицей будет
- 134. После логического умножения последних двух скобок и последующего упрощения получим: ррррррррррY=(A∨BC)(DE∨DF∨CEE∨CEF). Умножив оставшуюся пару скобок, получим
- 135. Для всех минимальных покрытий Sa=11; Sb=15. Минимальные ДНФ, соответствующие этим покрытиям:
- 136. МДНФ1: МДНФ2: МДНФ3: МДНФ4: Метод дальнейшего упрощения таблицы покрытий состоит в применении двух операций: а) вычеркивание
- 137. если множество меток i-й строки является подмно-жеством меток j-й строки и куб i имеет не большую
- 138. Процесс удаления “лишних” строк показан в таблице.. После удаления строк B и F, соответствующих максимальным кубам
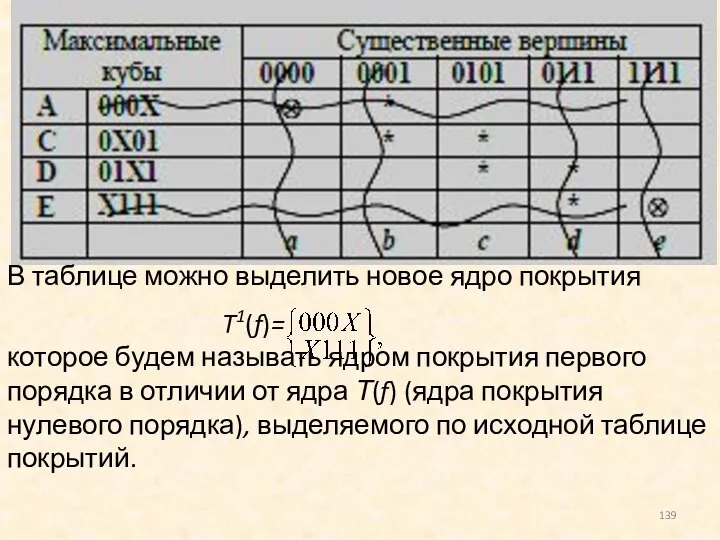
- 139. В таблице можно выделить новое ядро покрытия T1(f)= которое будем называть ядром покрытия первого порядка в
- 140. После вычеркивания кубов ядра T1(f) (строки A и E), а также существенных вершин, покрываемых кубами ядра
- 141. в то время, как с помощью метода Петрика найдены четыре минимальных покрытия, т.е. все возможные варианты.
- 142. Примером полной системы является S1 ={⎤ , &, ∨} (булев базис). Обоснованность утверждения о функциональной полноте
- 143. Другими примерами функционально полных систем являются системы из одной функции: S4={↓} (стрелка Пирса), S5={|} (штрих Шеффера),
- 144. Эта связь заключается в следующем: если каждой функ-ции из некоторой функционально полной системы сопо-ставить логический элемент,
- 145. Теорема о функциональной полноте (теорема Поста) Для того чтобы система булевых функций была функционально полной, необходимо
- 146. Эти классы называют замечательными классами булевых функций. Другая формулировка теоремы Поста: Для того, чтобы система булевых
- 147. К функциям, не сохраняющим ноль, относятся f(x)= и f(x1,x2)=x1~ x2. Булева функция называется сохраняющей единицу, если
- 148. В общем случае полином имеет вид: f n(Х) = K0 ⊕ K1x1 ⊕ ... ⊕ Kn
- 149. y= =1⊕ x (K0=K1=1, K2=0). Примеры нелинейных функций: y= x1⋅ x2, Булева функция называется монотонной, если
- 150. Примеры наборов, для которых имеет место отношение возрастания: (1011) > (0011); (1011) > (0001); (0001) >
- 151. Два набора аргументов называются противопо-ложными, если каждая из их компонент прини-мает противоположные значения, например, Х =
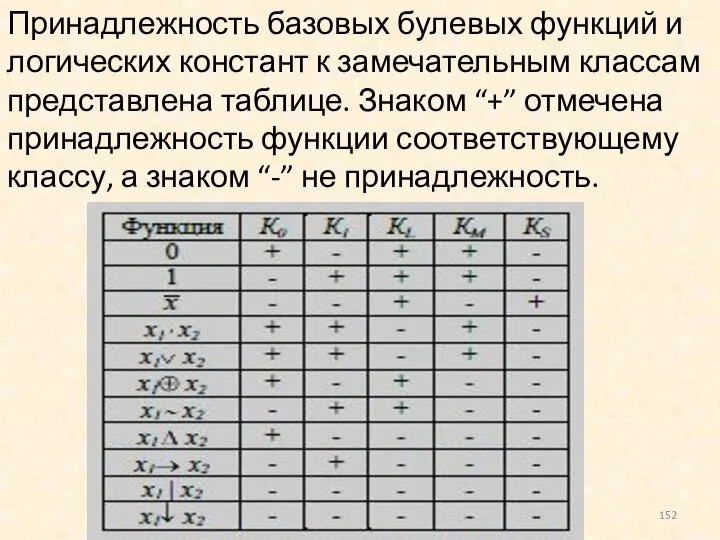
- 152. Принадлежность базовых булевых функций и логических констант к замечательным классам представлена таблице. Знаком “+” отмечена принадлежность
- 153. Из таблицы видно, что согласно теореме Поста, функции штрих Шеффера и стрелка Пирса являются функционально полными.
- 154. Теорема. Пусть система булевых функций {f1, …, fm} является функционально полной и любая из функций f1,
- 156. Скачать презентацию

































































































































 Признаки равенства треугольников
Признаки равенства треугольников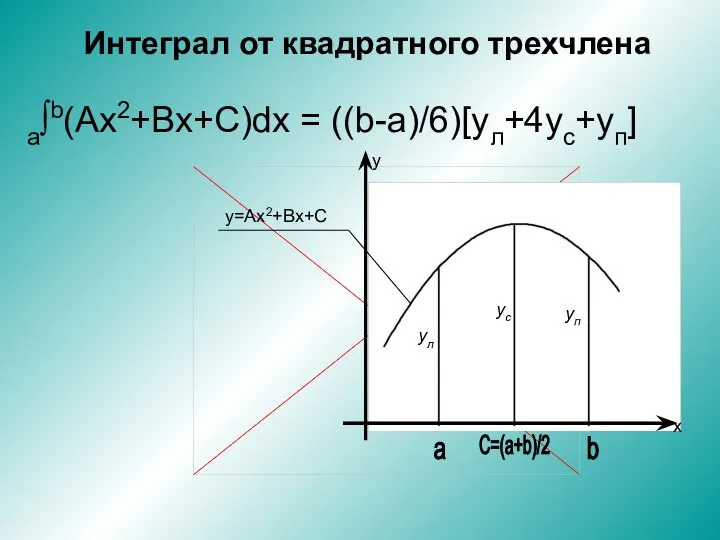 Интеграл от квадратного трехчлена
Интеграл от квадратного трехчлена Презентация на тему Из жизни геометрических фигур
Презентация на тему Из жизни геометрических фигур  Виды углов. (Задачи, 5 класс)
Виды углов. (Задачи, 5 класс) Свойства функций
Свойства функций Графический способ решения систем уравнений. Открытый урок по математике в 9 А классе
Графический способ решения систем уравнений. Открытый урок по математике в 9 А классе Тема «Решение задач на движение». Цели: Образовательные: обобщение знаний учащихся по теме «Решение задач на движение»; повыш
Тема «Решение задач на движение». Цели: Образовательные: обобщение знаний учащихся по теме «Решение задач на движение»; повыш Случаи деления вида 80:20
Случаи деления вида 80:20 Столько же и еще… Столько же, но без… Урок математики в 1 «Б» классе УМК «Перспектива» Мостовщикова О.А. МОУ «СОШ №5 город Саратов
Столько же и еще… Столько же, но без… Урок математики в 1 «Б» классе УМК «Перспектива» Мостовщикова О.А. МОУ «СОШ №5 город Саратов 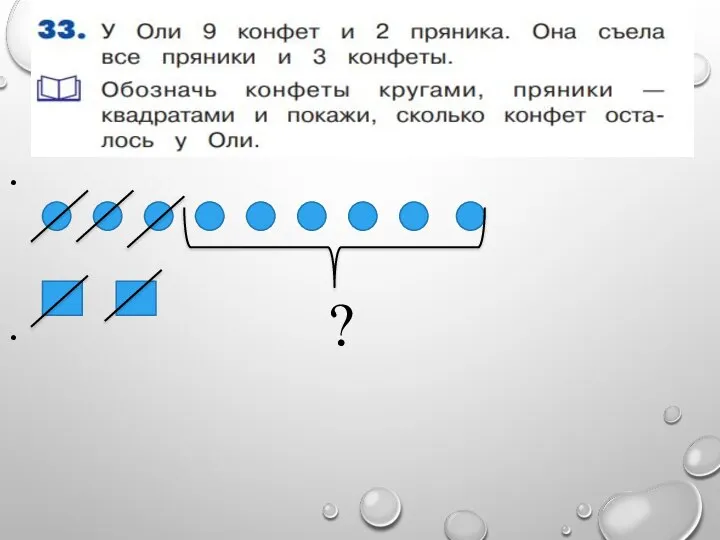 Задача № 33 по математике. 1 класс
Задача № 33 по математике. 1 класс Комбинаторика и ее применение
Комбинаторика и ее применение Анализ временных рядов
Анализ временных рядов Сложение и вычитание десятичных дробей, 5 класс
Сложение и вычитание десятичных дробей, 5 класс Задачи на нахождение наибольшего и наименьшего значений величин. 10 класс ( первый урок)
Задачи на нахождение наибольшего и наименьшего значений величин. 10 класс ( первый урок) Статистический анализ экспериментальных данных
Статистический анализ экспериментальных данных Презентация по математике "Противоположные числа" - скачать
Презентация по математике "Противоположные числа" - скачать  Численный анализ нелинейных моделей и теория Куна-Таккера (Лекция 5)
Численный анализ нелинейных моделей и теория Куна-Таккера (Лекция 5) Построение графика функции. Готовимся к ГИА
Построение графика функции. Готовимся к ГИА Проверка гипотез. Основы ДА
Проверка гипотез. Основы ДА Тригонометрия. Таблица значений тригонометрических функций
Тригонометрия. Таблица значений тригонометрических функций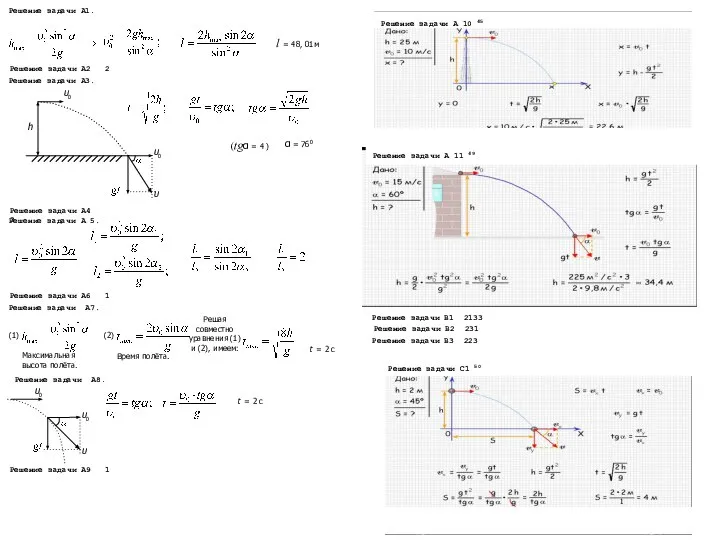 Ответы и решения.Решение задачи А1
Ответы и решения.Решение задачи А1 Метод десятичных матриц поиска
Метод десятичных матриц поиска Тригонометрические функции тупого угла
Тригонометрические функции тупого угла Линейное пространство. Базис. Линейная оболочка (УСР). Лекция 17
Линейное пространство. Базис. Линейная оболочка (УСР). Лекция 17 Задачи на совместную работу. 5 класс
Задачи на совместную работу. 5 класс Масштаб. 6 класс
Масштаб. 6 класс Презентация на тему Кратные интегралы
Презентация на тему Кратные интегралы  Математический счет
Математический счет